还是继续解决赛码网上的百度2017/2016秋招题目,选择了一些4星题目中比较有意思或者对知识有补充的题目写了解题分析,其他的题目我准备全部写完后,来个合集,做一个比较简单的解题报告。虽然是被标注为4星(百度的题目中没有5星),但是题目相对难度还是一般,或许因为这个题目是针对应届生,应该是大多数并没有从事算法竞赛的同学。但是无论难度如何,最好可以自己上手练习并提交测试。
第一天我们从一个简单的图论问题入手,实际上是讨论了一个最短路径相关问题,构图分析以后,使用了SPFA+heap优化的方式来完成目标
https://segmentfault.com/a/11...
这里我们仍然讨论一个最短路径的问题,因为不含有负权,我们使用dijkstra+heap优化的算法来最终解决问题。当然,也完全可以使用 SPFA,因为我们并没有修改算法本身。
赶火车
<题目来源:百度2017秋招,http://exercise.acmcoder.com/... >
问题描述
小A到达了一个陌生的城市,经过几天的功课,他已经知道了整个城市的公共交通情况。所有的公交设计都是完全对称的,公共汽车都是对向开行,且线路相同,对向开行的道路是同一条道路。小A所住的宾馆附近有a个公交车站,你知道火车站附近有b个公交车站。小A想知道从宾馆选定附近某个公交车站出发到火车站附近某一公交车站的最近的路程是多少。你能帮他吗
题目给定的目标还是比较容易达到的,我们只需要选择公交车站或者火车站顶点集合里面的每一个顶点求一次单源点最短路径,最后扫描另外一个集合里面的顶点,获取最小的单源点最短路径即可。
观察题目数据规模
*输入
输入数据有多组,第一行为一个正整数T(T<=20),表示测试数据组数,接下来包含T组测试数据。
每组测试数据第一行包含四个整数n(1<=n<=1000),m(0<=m< =n*(n-1)/2),a(1<=a<=n), b(1<=b<=n),分别表示城市中公交车站数、道路数目、宾馆附近公交车站数目和火车站附近的公交车站数目。
接下来一行包含a个整数si,si(1<=si<=n)表示宾馆附近的a个公交车站。
接下来一行包含b个整数ei,ei(1<=ei<=n)表示火车站附近的b个公交车站。
接下来m行每行包含三个整数u, v, w, (1<= u<= n, 1<= v<= n, u不等于v, 0<= w<10000)表示结点u和结点v之间存在一条长度为w的路径。(保证没有重边)*
根据a(1<=a<=n), b(1<=b<=n)这个条件,最坏的情况下我们可能需要计算n/2 + 1单源点最短路径(我们选择较小的一个集合里的点作为源点来计算最短路径,a,b两个集合不相交,也就是同一个顶点不会既是火车站公交车站,又是宾馆附近的公交车站,一旦相交那么结果为0,就不需要再计算),那么最坏情况下我们计算的时间复杂度O((|n|+|m|)*logn),并且dijkstra算法还需要使用heap优化。对于题目的数据规模而言,不能接受。
我们在稍微深入的分析下,在计算某一个源点的最短路径的时候所发生的情况,我们假设U={a, b, c}是酒店附近的公交车站,我们首先计算a的单源点最短路径,一种可能的情况是,a出发到x的最短路径可能是
a->b->...->c->...->x
我们发现一个有趣的现象,如果b, c在a->x的最短路径上,显然我们从c出发可以获得更短的路径,我们也并不关心从集合U中的哪个点出发,显然集合之间的点之间的边对我们最终的结果不产生影响,因为我们始终会选择一个更近的点来作为源点。
因此,我们可以考虑将U中的所有的点看做一个点,去掉集合内部顶点之间的边,保留集合U中任何顶点与不在U中的顶点的边,这些所有边都转为从一个点发出。这样的方法我们称之为缩点。
下面对缩点的前后的图进行了描述,其中红色表示需要去掉的边,绿色是保留下来的边。
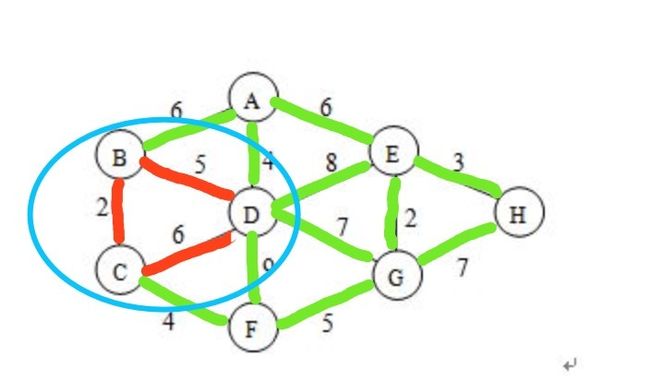
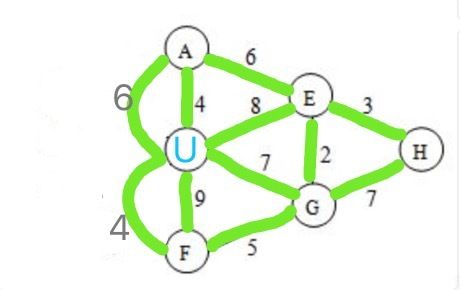
显然缩点以后我们需要进行一次单源点最短路径算法即可然后比较另外一个集合中的每个点的最短路径值即可。进一步,对于另外一个集合中的点,我们也可以进行同样的处理方法,这样可以减少一部分运算量,如果我把集合U中的点缩为1个点标号0,将另外一个集合T中的点缩为1个点,并且标号1,那么实际上我们是求解以0号点为源点,到达1号点的最短路径,考虑到这个是一个无向图并且不含有负权,我们采用了heap优化的dijkstra算法来实现我们最终的目标。
至此,在假设你已经掌握了dijkstra算法(不要求使用heap优化),那么最后一个需要解决的问题就是如何将集合中的点进行压缩。
1.对图中的点进行映射重新编号,例如集合U中原本为U={1,2,3,4},我们令map_v[1] = map_v[2] = map_v[3] = 1,也就是把原图上标号为1,2,3的顶点在新图上同一标为1,把另外一个集合T中原本的点标记为2,其余不在两个集合中的点,以此标为3,4,5...即可。
2.在读入图的时候,数据以u, v, w的形式给出,表示从顶点u有一条到顶点v的边,其权值为w,那么我们需要比较映射后的结果,如果map_v[u]=map_v[v],说明他们压缩后在同一个点(也就是这两个点在同一个集合中),我们不需要进行任何处理,反之,我们就像图中添加一条由map_v[u]到map_v[v]的权重为w的边,同时添加map_v[v]到map_v[u]的权重为w的边(别忘记这是一张无向图)
3.按映射后的图执行dijstra算法即可,最后得出结果即可。
至此,问题已经得到解决,下面会再简单介绍dijkstra算法正确证明和heap优化方法。但是这里并不打算详细的介绍dijkstra算法的原理和实现,如果需要学习推荐参考下面两篇文章:
http://wiki.mbalib.com/wiki/D...算法
http://www.cnblogs.com/shenbe...
大多数情况下我们并不需要关心如何去证明这些算法的正确性,但是dijkstra算法的证明比较简单,且有助于我们进一步理解算法。下面我就数学归纳法来进行一个简单的证明。
我们用集合U表示被dijkstra已经计算出最短路径dist[]的点:
a.首先考虑源点加入时的情况,源点加入时U中只有源点s,且dist[s] = 0,显然源点到源点的距离为0
b.当加入第1个点时,根据算法,选择了与s距离最近的一个点u来加入集合S,如果s->u的路径不是最短路径,那么必然还存在点p使得s->p->u距离更近,且edge(s,p) < edge(s, u),因此我们选择的时候就应该选择edge(s, p)而不是edge(s ,u),这与我们选择距离最近的点加入矛盾,故dist[u]是s到u的最短路径
c.当加入第k个点时,集合U中包含前k - 1个已经求出最短路径的点,考虑第k的加入时的情况,如果选择的k不是到源点的最短距离,那么必然在存在一个不在集合S中的点p使得
edge(i, p) + edge(p, k) < edge(i, k),那么edge(i, p) < edge(i, k),那么我们显然会选择edge(i, p),这个与我们选择距离最小的边矛盾
综上,到算法运行完毕时,U集合中的所有所有点的dist[]都是源点到该点的最短路径
最后,我们使用heap来优化
我们观察到,在dijkstra算法运行的时候,我们需要去寻找一个当前最小的dist[i],并且不在集合U的这样一个i点,并把i加入到集合中去。显然我们在不断更新dist的时候,可以维护一个小根堆,将更新得到的dist[i]和i的信息放入堆中,在需要获取最小dist的时候,我们从堆顶弹出顶点标号,只要这个顶点不在集合S中,我们就把这个顶点加入到集合中,并且去扩展计算与之相邻顶点的dist
提醒一个python的读入问题
python的raw_input()方式读入数据再行split(' ')切分会非常的慢,推荐使用map的方式,具体可以参见下面的代码部分。
import sys
import heapq
const_idx_vertex = 0
const_idx_wight = 1
def get_map_val(map_v, v, v_seq):
r = map_v.get(v)
if r is None:
v_seq[0] += 1
map_v[v] = v_seq[0]
r = v_seq[0]
return r
def dijkstra_with_heap(dist, src, n, vertexes):
dist[src] = 0
heap = []
S = set()
heapq.heappush(heap, (0, src))
for i in range(1, n):
while len(heap) > 0:
u = heapq.heappop(heap)[1]
if u not in S:
S.add(u)
break
for vertex in vertexes[u]:
v = vertex[const_idx_vertex]
w = vertex[const_idx_wight]
if dist[v] == -1 or dist[v] > dist[u] + w:
dist[v] = dist[u] + w
heapq.heappush(heap, (dist[v], v))
def main():
t_cases = int(raw_input())
for t_case in range(1, t_cases + 1):
n, m, a, b = map(int, sys.stdin.readline().strip().split())
map_v = {}
v_seq = [1]
line = map(int, sys.stdin.readline().strip().split())
for l in line:
map_v[l] = v_seq[0]
v_seq[0] += 1
line = map(int, sys.stdin.readline().strip().split())
for l in line:
map_v[l] = v_seq[0]
vertexes = [[]for i in range(n + 1)]
for i in range(m):
u, v, w = map(int, sys.stdin.readline().strip().split())
u = get_map_val(map_v, u, v_seq)
v = get_map_val(map_v, v, v_seq)
if u != v:
vertexes[u].append((v, w))
vertexes[v].append((u, w))
new_n = v_seq[0]
dist = [-1 for i in range(n + 1)]
dijkstra_with_heap(dist, 1, new_n, vertexes)
print 'Case #{}: '.format(t_case)
if dist[2] != -1:
print dist[2]
else:
print 'No answer'
if __name__ == '__main__':
main()