非线性光纤光学

%在色散位移光纤中得到结果与normal4比较，得出三阶色散对孤子对传输作用的影响

clear
clc

%?注意时间域与频域的选择问题
T = 40; %时间窗口                             
tn= 2^10;  % 时间区域个数（2^M个）                            
dt = T/tn;   %选择的时间步长  
t = ((1:tn)'-(tn+1)/2)*dt;  
w = wn(T,tn);%傅里叶域频率,调用计算频率函数 

b=0.03;
c=-i*w'.^2/2+i*b*w'.^3;
dz=0.1;  %迭代时选择的步长
%步长的选择影响计算效率
%z=0:dz:50;  % 位置坐标
z=0:dz:100;  % 位置坐标  

% 输入初始脉冲
q=3.5;r=1;o=0;%q为初始间距，r为相对振幅,o为相对相位
u(1,:)=sech(t-q)+r*sech(r*(t+q))*exp(i*o);  
%输入同幅同相孤子对

%?注意复数的表示，傅里叶变换函数的使用
%由于输入负频，fft对应逆变换，ifft对应傅里叶变换
for k=1:1:length(z)
% 分布傅里叶变换解方程
    u1=fft(exp(c*dz/2).*ifft(u(k,:)));
    u2=u1.*exp(i*dz*abs(u(k,:)).^2);
    u(k+1,:)=fft(exp(c*dz/2).*ifft(u2));
    %二次迭代
    for m=1:2
        u2=u1.*exp(i*dz/2*(abs(u(k,:)).^2+abs(u(k+1,:)).^2));
        u(k+1,:)=fft(exp(c*dz/2).*ifft(u2));
    end
%缺少迭代仿真将出现很多问题
end 

figure
subplot(1,2,1);
plot(t(1:1:length(t)),u(1,:),'k')
xlabel('归一化时间')
ylabel('归一化振幅')
axis([-20,20,0,1.5]);
title('DSF光纤中输入孤子对')

subplot(1,2,2);
mesh(t(1:1:length(t)),z(1:(length(z)-1)/50:length(z)-1),abs(u(1:(length(z)-1)/50:length(z)-1,:)))
%注意采样点少点好画，
view(-20,45);
xlabel('归一化时间')
ylabel('归一化距离')
zlabel('归一化振幅')
title('输出光脉冲')

%在色散位移光纤中得到结果与normal4比较，得出三阶色散对孤子对传输作用的影响

clear
clc

%?注意时间域与频域的选择问题
T = 20; %时间窗口(-10:10)                                
tn= 2^10;  % 时间区域个数（2^M个）                            
dt = T/tn;   %选择的时间步长  
t = ((1:tn)'-(tn+1)/2)*dt;  
w = wn(T,tn);%傅里叶域频率,调用计算频率函数 

b=0.03;
c=-i*w'.^2/2+i*b*w'.^3;
dz=0.1;  %迭代时选择的步长
%步长的选择影响计算效率
%z=0:dz:50;  % 位置坐标
z=0:dz:100;  % 位置坐标  

% 输入初始脉冲
q=3.5;r=1;o=0;%q为初始间距，r为相对振幅,o为相对相位
u(1,:)=sech(t-q)+r*sech(r*(t+q))*exp(i*o);  
%输入同幅同相孤子对

%?注意复数的表示，傅里叶变换函数的使用
%由于输入负频，fft对应逆变换，ifft对应傅里叶变换
for k=1:1:length(z)
% 分布傅里叶变换解方程
    u1=fft(exp(c*dz/2).*ifft(u(k,:)));
    u2=u1.*exp(i*dz*abs(u(k,:)).^2);
    u(k+1,:)=fft(exp(c*dz/2).*ifft(u2));
    %二次迭代
    for m=1:2
        u2=u1.*exp(i*dz/2*(abs(u(k,:)).^2+abs(u(k+1,:)).^2));
        u(k+1,:)=fft(exp(c*dz/2).*ifft(u2));
    end
%缺少迭代仿真将出现很多问题
    

%计算两个孤子间距离
        t1=0.0;
        t2=0.0;    
    for m=2:(length(t)-1)        
        u11=abs(u(k+1,m))-abs(u(k+1,m-1));
        u22=abs(u(k+1,m+1))-abs(u(k+1,m));
        u33=abs(u(k+1,m));
       if (u11>0)&(u22<0)&(u33>0.5)           
           if (t1==0)&(t2==0)
               t1=t(m);   %(m-1)*Ts;
           elseif (t1~=0)&(t2==0)               
               t2=t(m); %(m-1)*Ts;
           end
       end         
   end
   if t2==0
      t2=t1;
   end   
  td(k+1)=t2-t1;
  


end 



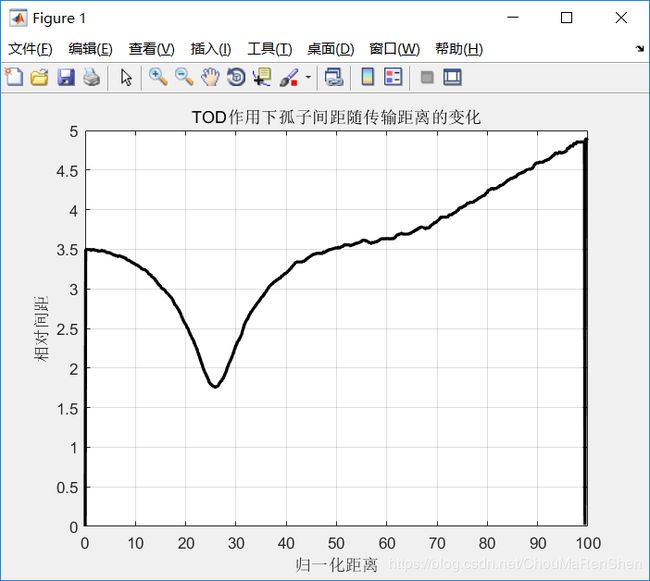
plot(z(1:length(z)-1),abs(td(1:length(z)-1))/2,'k','linewidth',2);
title('TOD作用下孤子间距随传输距离的变化');
xlabel('归一化距离');
ylabel('相对间距');
hold on
grid on