非线性光纤光学——四波混频
四波混频:基于X(3)非线性效应的光的相互作用
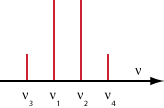
- 四波混频是一种基于三阶光学非线性(由X(3)系数描述)的非线性效应。当有至少两个不同频率分量的光一同在非线性介质(如光纤)中传播时就有可能发生四波混频效应。假设输入光中有两个频率分量v1和v2(v2>v1),由于差频的折射率调制的存在,会产生两个新的频率分量(如图1所示):v3=v1-(v2-v1)=2v1-v2和v4=v2+(v2-v1)=2v2-v1。此时如果原先就存在v3或v4分量,则表现为v3或v4被放大,即这个两个频率分量经历了参量放大。
- 当四波混频作用涉及四个不同的频率分量时,其为非简并的四波混频。当然还存在简并的四波混频,即四波混频中的两个频率重合。例如,可以利用一个单频的泵浦作为一个临近波长的信号光的放大源,在这个四波混频过程中,每有一个光子被增加到信号光中(即实现放大)时,都会使用两个泵浦波长的光子,另外还在泵浦光波长的另一侧产生一个闲散波的光子。
- 四波混频过程是对相位非常敏感的(即四波混频作用依赖于涉及到的所有光的相对相位)。当激光在光纤等介质中满足相位匹配的条件时,四波混频作用会随着传播距离的增加而有效的增强。相位匹配的条件意味着四波混频中的各个分量的频率很接近或者介质有一个合适的色散曲线。当相位严重不匹配时,四波混频作用会被大大地抑制。在固体介质中,还可以通过调节不同光束之间的方向和角度来实现相位匹配。
- 光纤中的四波混频作用是与自相位调制和交叉相位调制密切相关的,这些效应都是由同一个非线性效应(克尔效应)造成的,只不过每个效应中的光的频率的简并状态不同。
四波混频在不同的情况下有不同的作用,例如:
- 其会参与到一些光纤放大器(如:纳秒脉宽量级的光纤放大器)中的光谱展宽。在某些应用中,这种光谱展宽作用是很强的,甚至会产生超连续谱。超连续谱产生的过程涉及到很多种不同的非线性作用,而四波混频会在长脉冲的超连续谱产生中起到很大的作用;
- 基于四波混频的参量放大可以用于光纤的光学参量放大器(OPA)和光学参量振荡器(OPO)中。在这种情况下ν_1和ν_2是重叠的。相比于基于χ^((2))非线性效应的光学参量放大器和光学参量振荡器,这种基于四波混频效应的设备中的泵浦光的频率是在信号光和闲散光之间的;
- 四波混频作用在光纤通信中通常是有害的,特别在波分复用技术中,四波混频会造成不同信道之间的串扰和信道功率的不平衡。通过使用非等间隔的信道可以抑制该效应;
- 在光谱学中,四波混频通常出现在相干反斯托克斯拉曼光谱学中。在这种方法中,两个输入光波会产生一个频率略高于输入光的被探测信号。通过改变输入光束的时间延迟,还可以测量激发态寿命和退相率。
- 四波混频还被应用于相位共轭、全息成像和光学图像处理等技术中。
clc;
clear all;
close all;
% burst = [1 , 1,1,1,1,1,-1,-1,1,1,-1,1,-1,1 , -1,-1,-1,-1,-1,1,1,-1,-1,1,-1,1,-1];
burst = sign(randn(1 , 1000));
% Tb = 3.692e-6;
Tb = 1/19200;
OSR= 16;
BT = 0.3;
Ts = Tb/OSR;
% PREPARING VECTORS FOR DATA PROCESSING
%
PTV = -2*Tb:Ts:2*Tb;
RTV = -Tb/2:Ts:Tb/2;
% GENERATE GAUSSIAN SHAPED PULSE
%
sigma = sqrt(log(2))/(2*pi*BT);
gauss = (1/(sqrt(2*pi)*sigma*Tb))*exp(-PTV.^2/(2*sigma^2*Tb^2));
% GENERATE RECTANGULAR PULSE
%
rect = 1/(2*Tb)*ones(size(RTV));
% CALCULATE RESULTING FREQUENCY PULSE
%
G_TEMP = conv(gauss,rect);
% TRUNCATING THE FUNCTION TO 3xTb
%
G = G_TEMP(OSR+1:4*OSR);
% TRUNCATION IMPLIES THAT INTEGRATING THE FREQUENCY PULSE
% FUNCTION WILL NOT EQUAL 0.5, HENCE THE RE-NORMALIZATION
%
G_FUN = (G-G(1))./(2*sum(G-G(1)));
% CALCULATE RESULTING PHASE PULSE
%
Q_FUN = cumsum(G_FUN);
h = 0.5;
phi(1 : OSR) = 2*pi*h*burst(1) .* Q_FUN(1 : OSR);
phi(1+OSR : 2*OSR) = 2*pi*h*burst(2) .* Q_FUN(1 : OSR) + 2*pi*h*burst(1) .* Q_FUN(1+OSR : 2*OSR);
phi(1+2*OSR : 3*OSR) = 2*pi*h*burst(3) .* Q_FUN(1 : OSR) + 2*pi*h*burst(2) .* Q_FUN(1+OSR : 2*OSR) + ...
2*pi*h*burst(1) .* Q_FUN(1+2*OSR : 3*OSR);
for i = 4 : length(burst)
phi(1+(i-1)*OSR : i*OSR) = 2*pi*h*burst(i) .* Q_FUN(1 : OSR) + 2*pi*h*burst(i-1) .* Q_FUN(1+OSR : 2*OSR) + ...
2*pi*h*burst(i-2) .* Q_FUN(1+2*OSR : 3*OSR) + pi*h*sum(burst(1:i-3));
end
GMSK = exp(j.*phi);
gt = ones(1,OSR);
for i = 1 : OSR
Q_FUN2(i) = sum(gt(1:i));
end
Q_FUN2 = 0.5 / max(Q_FUN2) .* Q_FUN2;
phi2(1 : OSR) = 2*pi*h*burst(1) .* Q_FUN2;
for i = 2 : length(burst)
phi2(1+(i-1)*OSR : i*OSR) = 2*pi*h*burst(i) .* Q_FUN2 + pi*h*sum(burst(1:i-1));
end
MSK = exp(j.*phi2)