JS操作SVG模拟水滴分离、融合效果
很多的App应用下拉刷新使用拉拽圆的动态效果来表示下拉过程,很富有表现性;还有QQ的消除红点的过程等,都使用到了这种类似水滴融合的效果。
这种变化的实质是绘制两个圆,然后在两个圆之间利用贝塞尔曲线来描绘弧形,在两个圆的距离随着拖动发生改变时,通过计算数学公式动态地更改曲线的弧度,从而使整个变化过程看起来更加协调。
下面粗略模拟一下这个过程,如果想要更加完美的表现,需要经过精确的计算得出更准确的公式,这里之后补充。
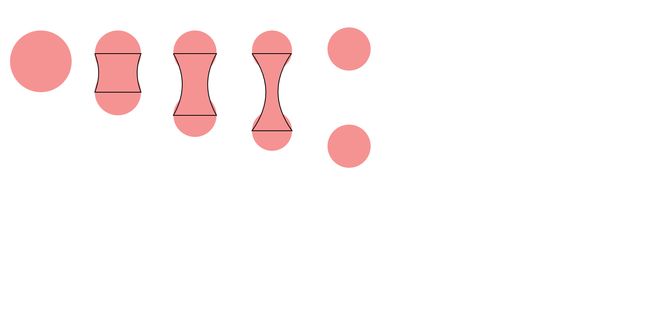
首先我们绘制一下变化过程中的几个过程,如下图:
两个圆之间的粘合部分需要使用二次贝塞尔曲线来绘制。其中弧线的两个端点值和一个中间点,目前使用竖直线和圆的切线交点和两个圆心中点的水平线上偏移一定值的点来简单替代,当然效果不够完美,有待后续优化。例如第二个图的路径写法如下:
<g transform="translate(100,0)">
<circle cx="100" cy="100" r="30" fill="#f59393">circle>
<circle cx="100" cy="150" r="30" fill="#f59393">circle>
<path d="M70,100 Q80,125 70,150 L130,150 Q120,125 130,100 L70,100" fill="#f59393" stroke="black">path>
g>在图中标志下路径:
通过模拟上面几个大致的变化过程,得出粗略的公式,绑定点击事件,实现分离、融合效果:
下面是代码:
<html>
<head>
<meta charset="utf-8">
<title>SVG模拟水滴分离、融合效果title>
head>
<body>
<svg width="800" height="400" id="svg">
<g transform="translate(0,0)">
<circle cx="100" cy="110" r="40" fill="#f59393">circle>
g>
<g transform="translate(100,0)">
<circle cx="100" cy="100" r="30" fill="#f59393">circle>
<circle cx="100" cy="150" r="30" fill="#f59393">circle>
<path d="M70,100 Q80,125 70,150 L130,150 Q120,125 130,100 L70,100" fill="#f59393">path>
g>
<g transform="translate(200,0)">
<circle cx="100" cy="98" r="28" fill="#f59393">circle>
<circle cx="100" cy="180" r="28" fill="#f59393">circle>
<path d="M72,100 Q95,140 72,180 L128,180 Q105,140 128,100 L72,100" fill="#f59393">path>
g>
<g transform="translate(300,0)">
<circle cx="100" cy="96" r="26" fill="#f59393">circle>
<circle cx="100" cy="200" r="26" fill="#f59393">circle>
<path d="M74,100 Q110,150 74,200 L126,200 Q90,150 125,100 L74,100" fill="#f59393">path>
g>
<g transform="translate(400,0)">
<circle cx="100" cy="94" r="28" fill="#f59393">circle>
<circle cx="100" cy="220" r="28" fill="#f59393">circle>
g>
<g transform="translate(500,0)" id="g">
<circle id="circle1" cx="100" cy="110" r="40" fill="#f59393">circle>
<circle id="circle2" cx="100" cy="110" r="40" fill="#f59393">circle>
<path id="path" fill="#f59393">path>
g>
<g transform="translate(600,0)" id="g2">
<circle id="circle3" cx="100" cy="94" r="28" fill="#f59393">circle>
<circle id="circle4" cx="100" cy="216" r="28" fill="#f59393">circle>
<path id="path2" fill="#f59393">path>
g>
svg>
<button id="split">分离button>
<button id="split2">合并button>
<script type="text/javascript">
var svg = document.getElementById("svg");
var g = document.getElementById("g");
var circle = document.getElementById("circle1");
var circle2 = document.getElementById("circle2");
var path = document.getElementById("path");
var g2 = document.getElementById("g");
var circle3 = document.getElementById("circle3");
var circle4 = document.getElementById("circle4");
var path2 = document.getElementById("path2");
var button = document.getElementById("split");
var button2 = document.getElementById("split2");
button.onclick = function(){
for(var i=1;i<=40;i++){
(function(i){
setTimeout(function(){
i /=10;
var cx = parseInt(circle1.getAttribute("cx"));
var cy1 = 102-i*2;
var cy2 = 120+(i>2?(i+1)*20:i*30);
var r = 32-i*2;
var q1 = 65+i*15;
var q2 = 135-i*15;
//防止弧线交叉
if(q1>=q2+45){
path.setAttribute("d","");
circle1.setAttribute("r",28);
circle2.setAttribute("r",28);
return;
}else{
circle1.setAttribute("cy",cy1);
circle1.setAttribute("r",r);
circle2.setAttribute("cy",cy2);
circle2.setAttribute("r",r);
path.setAttribute("d","M"+(cx-r)+",100 Q"+q1+","+((cy1+cy2)/2)+
" "+(cx-r)+","+cy2+" L"+(cx+r)+","+cy2+" Q"+q2+","+((cy1+cy2)/2)+
" "+(cx+r)+",100 L72,100");
}
},i*20)})(i);
}
};
button2.onclick = function(){
for(var i=40;i>=0;i--){
(function(i){
setTimeout(function(){
i /=10;
var cx = parseInt(circle3.getAttribute("cx"));
var cy1 = 102-i*2;
var cy2 = 120+(i>2?(i+1)*20:i*30);
var r = 32-i*2;
var q1 = 65+i*15;
var q2 = 135-i*15;
if(i<=0){
circle3.setAttribute("cy",110);
circle3.setAttribute("r",40);
circle4.setAttribute("cy",110);
circle4.setAttribute("r",40);
path2.setAttribute("d","");
}else{
//防止弧线交叉
if(q1>=q2+45){
console.log(i)
path2.setAttribute("d","");
return;
}else{
circle3.setAttribute("cy",cy1);
circle3.setAttribute("r",r);
circle4.setAttribute("cy",cy2);
circle4.setAttribute("r",r);
path2.setAttribute("d","M"+(cx-r)+",100 Q"+q1+","+((cy1+cy2)/2)+
" "+(cx-r)+","+cy2+" L"+(cx+r)+","+cy2+" Q"+q2+","+((cy1+cy2)/2)+
" "+(cx+r)+",100 L72,100");
}
}
},(40-i)*20)})(i);
}
}
script>
body>
html>