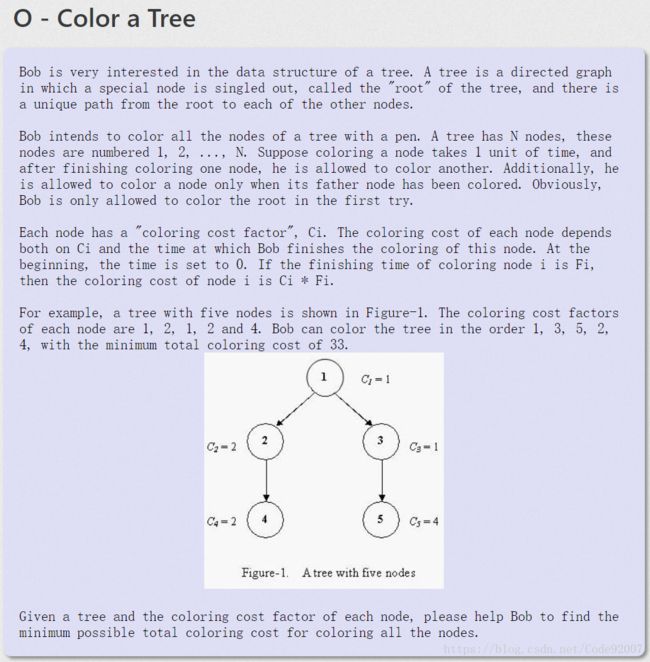
hdu1055 Color a tree(贪心☆☆☆☆☆)

思路来源

来源①：https://blog.csdn.net/gatieme/article/details/49202739

来源②：https://www.cnblogs.com/dramstadt/p/3201984.html

题意

给你一棵树，一上来可以染根节点。

对于其他的点i，染i时必须先染i的父节点。

每个点i对应一个权值c[i]，

从t=0开始染色，染i的花费=c[i]*当前时间t

现给定父子关系和根节点编号，

不妨设点i在s[i]秒被染色，染色时间为1(这里记为t[i])

即求

题解

显然，我们染了一个点之后，

如果它的后继点是权值最大的点，

我们立刻染权值最大的点，是最明智的选择。

 

这就意味着，不管何时染权值最大的点的前驱，

染完之后下一秒都该染权值最大的点，

即在染色序列中，权值最大的点是和它的前驱挨在一起的。

我们把这两个点绑定在一起，合二为一。

 

记点i在s[i]秒被染色，染色时间为t[i]，权值为c[i]，

考虑三个点的情形x y z

其中x是y的前驱，z可以直接染。

这样有两种染色方式，

c[x]+2c[y]+3c[z]①

c[z]+2c[x]+3c[y]②

 

在任意一种染色方式中，y都在x后染，

设第s[x]秒染x，cost为s[x]·c[x]

则(s[x]+1)秒染y，cost为(s[x]+1)·c[y]，在这里t[x]=1,

如果我们将x和y绑定在一起的话直接求s[x]*(c[x]+c[y])，会少算1·c[y]

因此，我们每一次合并，就把染父亲节点所需时间*子节点的权值（这里是t[x]*c[y]）加到sum里。

 

此外，若先不考虑随时间增长的花费，

它们都至少有c[x]+c[y]+c[z]的基础花费，我们在最初的时候把这些也加到sum里。

而选择任意一种方式，都会有y在x后染而带来的附加花费c[y]

这样最基础的花费就是c[x]+2c[y]+c[z]

 

比较基础花费和①、②的区别，发现一个多2*c[z]，另一个多(c[x]+c[y])

假设这里c[x]+c[y]<2*c[z]，

那么我们就应该选策略②，让z先染，

其实质是，即单染z的时间比染x、y的平均时间长，

因此，我们优先染那些平均单点时间长的点。

 

事实上，由于c[z]大，先将z向根合并，再将(xy)合点向根合并，就达到了先染z的目的。

而实际由于先合并z的时候，根节点里只有一个点，

再合并xy的时候，根节点里有两个点，

所以对答案的贡献，大的权值*1+小的权值*2，一定比反过来更优。

这实际上，就是第一秒染z，第二秒染xy合点（由于sum里加过c[y]其实是第二秒染x第三秒染y）的等价意义。

 

所以，开一个结构体，代表节点/合并后的节点

记录一个c，是合并点的总权值，

记录一个t，是合并点的染点总时间

每次遍历选择，v=c/t最大的，即平均时间最大的点开始染。

 

怎么叫染了这个点呢？把它和它的父节点合并。

代表染完它的祖先节点之后，立刻染这个点。

 

代码

#include 
#include  
#include 
#include 
#include 
#include 
#include