Range Sum Query Immutable
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
Example:
Given nums = [-2, 0, 3, -5, 2, -1]
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
Note:
You may assume that the array does not change.
There are many calls to sumRange function.假设有一个整数数组，计算下标从i到j（包含i和j）的数字的和。求和的请求将会在同一个整数数组上多次请求。
这一题思路很简单，因为sum[i-j] = sum[0~j] - sum[0~(i-1)]。我们只需要通过一圈遍历计算出每个下标至0的所有数字的和即可。而利用动态规划则很容易知道sum[0~j] = sum[0~j-1] + num[j]。
private int[] sum;
public NumArray(int[] nums) {
this.sum = new int[nums.length];
for(int i = 0 ; iRange Sum Query Immutable II
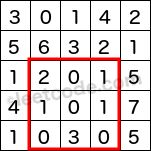
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Range Sum Query 2D
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
Note:
You may assume that the matrix does not change.
There are many calls to sumRegion function.
You may assume that row1 ≤ row2 and col1 ≤ col2.这里将原先的一维数组替换成二维数组。要求计算一个矩形内的所有元素的值。
其实思路还是和原来一样的，sum(row1, column1, row2, column2) = sum(0,0,row2, col1-1) + sum(0,0,row1-1, col2) - sum(0,0,row1-1, col1-1)。这里需要排除一些特殊情况，比如row1=1或是col1=1等。
private int[][] sum;
public NumMatrix(int[][] matrix){
int row = matrix.length;
if(row==0) {sum = new int[0][0]; return;}
int column = matrix[0].length;
sum = new int[row][column];
for(int i = 0 ; i0? sum[row1-1][col2] : 0 )- (col1>0 ? sum[row2][col1-1] : 0) + (row1>0 && col1>0 ? sum[row1-1][col1-1] : 0);
}
想要了解更多开发技术，面试教程以及互联网公司内推，欢迎关注我的微信公众号！将会不定期的发放福利哦~