一. 引言
Druid 的查询需要有实时和历史部分的 Segment,历史部分的 Segment 由 Historical 节点加载,所以加载的效率直接影响了查询的 RT(不考虑缓存)。查询通常需要指定一个时间范围[StartTime, EndTime],该时间范围的内所有 Segment 需要由 Historical 加载,最差的情况是所有 Segment 不幸都储存在一个节点上,加载无疑会很慢;最好的情况是 Segment 均匀分布在所有的节点上,并行加载提高效率。所以 Segment 在 Historical 集群中分布就变得极为重要,Druid 通过 Coordinator 的 Balance 策略协调 Segment 在集群中的分布。
本文将分析 Druid 的 Balance 策略、源码及其代价计算函数,本文使用 Druid 的版本是 0.12.0。
二. Balance方法解析
2.1 Balance 相关的配置
Druid 目前有三种 Balance 算法: cachingCost, diskNormalized, Cost, 其中 cachingCost 是基于缓存的,diskNormalized 则是基于磁盘的 Balance 策略,本文不对前两种展开篇幅分析, Druid Coordinator 中开启 cost balance 的配置如下:
druid.coordinator.startDelay=PT30S
druid.coordinator.period=PT30S 调度的时间
druid.coordinator.balancer.strategy=cost 默认
动态配置:
maxSegmentsToMove = 5 ##每次Balance最多移动多少个Segment2.2 Cost 算法概述
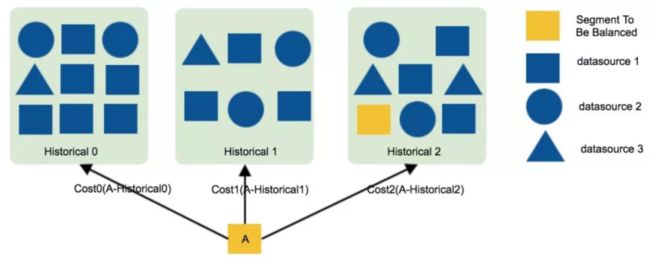
Cost 是 Druid 在 0.9.1 开始引入的,在 0.9.1 之前使用的 Balance 算法会存在 Segment 不能快速均衡,分布不均匀的情况,Cost 算法的核心思想是:当在做均衡的时候,随机选择一个 Segment(假设 Segment A ), 依次计算Segment A 和 Historical 节点上的所有 Segment 的 Cost,选取 Cost 值最小的节点,然后到该节点上重新加载 Segment
2.3 源码和流程图分析
以下会省略一些不必要的代码
DruidCoordinatorBalancer 类
@Override
public DruidCoordinatorRuntimeParams run(DruidCoordinatorRuntimeParams params)
{
final CoordinatorStats stats = new CoordinatorStats();
// 不同tier层的分开Balance
params.getDruidCluster().getHistoricals().forEach((String tier, NavigableSet servers) -> {
balanceTier(params, tier, servers, stats);
});
return params.buildFromExisting().withCoordinatorStats(stats).build();
} DruidCoordinatorBalancer 类的 balanceTier 方法,主要是均衡入口函数
private void balanceTier(DruidCoordinatorRuntimeParams params, String tier, SortedSet servers,CoordinatorStats stats){
final BalancerStrategy strategy = params.getBalancerStrategy();
final int maxSegmentsToMove = params.getCoordinatorDynamicConfig().getMaxSegmentsToMove();
currentlyMovingSegments.computeIfAbsent(tier, t -> new ConcurrentHashMap<>());
final List serverHolderList = Lists.newArrayList(servers);
//集群中只有一个 Historical 节点时不进行Balance
if (serverHolderList.size() <= 1) {
log.info("[%s]: One or fewer servers found. Cannot balance.", tier);
return;
}
int numSegments = 0;
for (ServerHolder server : serverHolderList) {
numSegments += server.getServer().getSegments().size();
}
if (numSegments == 0) {
log.info("No segments found. Cannot balance.");
return;
}
long unmoved = 0L;
for (int iter = 0; iter < maxSegmentsToMove; iter++) {
//通过随机算法选择一个候选Segment,该Segment会参与后面的Cost计算
final BalancerSegmentHolder segmentToMove = strategy.pickSegmentToMove(serverHolderList);
if (segmentToMove != null && params.getAvailableSegments().contains(segmentToMove.getSegment())) {
//找Cost最小的节点,Cost计算入口
final ServerHolder holder = strategy.findNewSegmentHomeBalancer(segmentToMove.getSegment(), serverHolderList);
//找到候选节点,发起一次Move Segment的任务
if (holder != null) {
moveSegment(segmentToMove, holder.getServer(), params);
} else {
++unmoved;
}
}
}
......
} Reservoir 随机算法,随机选择一个 Segment 进行 Balance。Segment 被选中的概率:
public class ReservoirSegmentSampler
{
public BalancerSegmentHolder getRandomBalancerSegmentHolder(final List serverHolders)
{
final Random rand = new Random();
ServerHolder fromServerHolder = null;
DataSegment proposalSegment = null;
int numSoFar = 0;
//遍历所有List上的Historical节点
for (ServerHolder server : serverHolders) {
//遍历一个Historical节点上所有的Segment
for (DataSegment segment : server.getServer().getSegments().values()) {
int randNum = rand.nextInt(numSoFar + 1);
// w.p. 1 / (numSoFar+1), swap out the server and segment
// 随机选出一个Segment,后面的会覆盖前面选中的,以最后一个被选中为止。
if (randNum == numSoFar) {
fromServerHolder = server;
proposalSegment = segment;
}
numSoFar++;
}
}
if (fromServerHolder != null) {
return new BalancerSegmentHolder(fromServerHolder.getServer(), proposalSegment);
} else {
return null;
}
}
} 继续调用到CostBalancerStrategy类的findNewSegmentHomeBalancer方法,其实就是找最合适的Historical节点
@Override
public ServerHolder findNewSegmentHomeBalancer(DataSegment proposalSegment, List serverHolders){
return chooseBestServer(proposalSegment, serverHolders, true).rhs;
}
protected Pair chooseBestServer(
final DataSegment proposalSegment,
final Iterable serverHolders,
final boolean includeCurrentServer
){
Pair bestServer = Pair.of(Double.POSITIVE_INFINITY, null);
List>> futures = Lists.newArrayList();
for (final ServerHolder server : serverHolders) {
futures.add(
exec.submit(
new Callable>()
{
@Override
public Pair call() throws Exception
{
//计算Cost:候选Segment和Historical节点上所有Segment的cost和
return Pair.of(computeCost(proposalSegment, server, includeCurrentServer), server);
}
}
)
);
}
final ListenableFuture>> resultsFuture = Futures.allAsList(futures);
final List> bestServers = new ArrayList<>();
bestServers.add(bestServer);
try {
for (Pair server : resultsFuture.get()) {
if (server.lhs <= bestServers.get(0).lhs) {
if (server.lhs < bestServers.get(0).lhs) {
bestServers.clear();
}
bestServers.add(server);
}
}
//Cost最小的如果有多个,随机选择一个
bestServer = bestServers.get(ThreadLocalRandom.current().nextInt(bestServers.size()));
}
catch (Exception e) {
log.makeAlert(e, "Cost Balancer Multithread strategy wasn't able to complete cost computation.").emit();
}
return bestServer;
} protected double computeCost(final DataSegment proposalSegment, final ServerHolder server,final boolean includeCurrentServer){
final long proposalSegmentSize = proposalSegment.getSize();
// (optional) Don't include server if it is already serving segment
if (!includeCurrentServer && server.isServingSegment(proposalSegment)) {
return Double.POSITIVE_INFINITY;
}
// Don't calculate cost if the server doesn't have enough space or is loading the segment
if (proposalSegmentSize > server.getAvailableSize() || server.isLoadingSegment(proposalSegment)) {
return Double.POSITIVE_INFINITY;
}
// 初始cost为0
double cost = 0d;
//计算Cost:候选Segment和Historical节点上所有Segment的totalCost
cost += computeJointSegmentsCost(
proposalSegment,
Iterables.filter(
server.getServer().getSegments().values(),
Predicates.not(Predicates.equalTo(proposalSegment))
)
);
// 需要加上和即将被加载的Segment之间的cost
cost += computeJointSegmentsCost(proposalSegment, server.getPeon().getSegmentsToLoad());
// 需要减掉和即将被加载的 Segment 之间的 cost
cost -= computeJointSegmentsCost (proposalSegment, server.getPeon().getSegmentsMarkedToDrop());
return cost;
}开始计算:
static double computeJointSegmentsCost(final DataSegment segment, final Iterable segmentSet){
double totalCost = 0;
// 此处需要注意,当新增的Historical节点第一次上线的时候,segmentSet应该是空,所以totalCost=0最小
// 新增节点总会很快的被均衡
for (DataSegment s : segmentSet) {
totalCost += computeJointSegmentsCost(segment, s);
}
return totalCost;
} 进行一些处理:1)Segment的Interval毫秒转换成hour; 2)先计算了带lambda的x1, y0, y1的值
public static double computeJointSegmentsCost(final DataSegment segmentA, final DataSegment segmentB){
final Interval intervalA = segmentA.getInterval();
final Interval intervalB = segmentB.getInterval();
final double t0 = intervalA.getStartMillis();
final double t1 = (intervalA.getEndMillis() - t0) / MILLIS_FACTOR; //x1
final double start = (intervalB.getStartMillis() - t0) / MILLIS_FACTOR; //y0
final double end = (intervalB.getEndMillis() - t0) / MILLIS_FACTOR; //y1
// constant cost-multiplier for segments of the same datsource
final double multiplier = segmentA.getDataSource().equals(segmentB.getDataSource()) ? 2.0 : 1.0;
return INV_LAMBDA_SQUARE * intervalCost(t1, start, end) * multiplier;
}真正计算 cost 函数的值
public static double intervalCost(double x1, double y0, double y1){
if (x1 == 0 || y1 == y0) {
return 0;
}
// 保证Segment A开始时间小于B的开始时间
if (y0 < 0) {
// swap X and Y
double tmp = x1;
x1 = y1 - y0;
y1 = tmp - y0;
y0 = -y0;
}
if (y0 < x1) {
// Segment A和B 时间有重叠的情况,这个分支暂时不分析
.......
} else {
// 此处就是计算A和B两个Segment之间的cost,代价计算函数:See https://github.com/druid-io/druid/pull/2972
final double exy0 = FastMath.exp(x1 - y0);
final double exy1 = FastMath.exp(x1 - y1);
final double ey0 = FastMath.exp(0f - y0);
final double ey1 = FastMath.exp(0f - y1);
return (ey1 - ey0) - (exy1 - exy0);
}
}2.4 代价计算函数分析
现在我们有 2 个 Segment, A 和 B,需要计算他们之间的代价,假设 A 的 start 和 end 时间都是小于 B 的。
2.4.1 Cost函数介绍
Cost 函数的提出请参考 Druid PR2972:
$$Cost(X, Y)=\\int\_{x\_0}^{x\_1}\\int\_{y\_0}^{y\_1} {e^{\\lambda|x-y|}}\\,{\\rm d}x{\\rm d}y$$
其中 \( \lambda = frac{log_2e}{24.0} \) 是Cost函数的半衰期
为了弄清楚这个 Cost 函数以及影响 Cost 值的因素?我们先使用一些常用的参数配置:
假设1:Segment A 的Interval是1小时,即 \( A_{end}-A_{start}=1*Hour \), 得到:
$$x\_1 = \\frac{(A\_{end}-A\_{start})\*log\_e2}{24*Hour} = \\frac{log\_e2}{24}$$
假设2:Segment B 的 Interval 也是 1 小时, 得到:
$$y\_1 = y\_0 + x\_1$$
假设3:Segment B 和 A start 时间相差了 t 个小时,得到:
$$y\_0 = \\frac{t\*Hour\*log\_e2}{24*Hour} = \\frac{t}{24}\*log\_e2$$
在实际的代码中,\( \lambda \)的计算已经放到了\( {x_0}{x_1}{y_0}{y_1} \)中
2.4.2 计算 Cost 函数
$$Cost(A, B)=(e^{x\_1-y\_0}-e^{x\_1-y\_1})-(e^{-y\_0}-e^{-y\_1})$$
根据假设 2,得到:
$$Cost(A, B)=(e^{x\_1 - y\_0} - e^{-y\_0}) - (e^{-y\_0} - e^{-x\_1 - y\_0})=e^{x\_1 - y\_0} + e^{-x\_1 - y\_0} - 2e^{-y\_0}$$
继续简化,得到:
$$Cost(A, B)=(e^{x\_1} + e^{-x\_1} - 2 )e^{-y\_0}$$
根据假设 1,得到:
$$Cost(A, B)=(2^{\\frac{1}{24}} + 2^{-\\frac{1}{24}} - 2)e^{-y\_0}$$
根据假设 3,得到:
$$Cost(A, B)=(2^{\\frac{1}{24}} + 2^{-\\frac{1}{24}} - 2)*e^{\\frac{-t}{24} * log\_e2}$$
继续简化,得到:
$$ Cost(A, B)={(2^{\frac{1}{24}} + 2^{-\frac{1}{24}} - 2)*2^{\frac{-t}{24}}}$$
2.4.5 小结
根据上诉 cost 函数化简的结果,当 Segment A 和 B 的 Interval 都是 1 小时的情况下:Segment A 和 B 时间相距越大 Cost 越小,它们就越可能共存在同一个 Historical 节点。这也和本文开始时候提出的时间相邻的 Segment 存储在不同的节点上让查询更快相呼应。
三. 总结
Druid 的 balance 机制,主要解决 segments 数据在 history 节点的分布问题,这里的优化主要针对于查询做优化,一般情况下,用户的某一次查询针对的是一个时间范围内的多个 Segment 数据, cost 算法的核心思想是,尽可能打散 Segment 数据分布,这样在一次查询设计多个连续时间 Segment 数据的时候能够利用多台 history server 的并行处理能力,分散系统开销,缩短查询 RT.
最后打个小广告,有赞大数据团队基础设施团队,主要负责有赞的数据平台(DP), 实时计算(Storm, Spark Streaming, Flink),离线计算(HDFS,YARN,HIVE, SPARK SQL),在线存储(HBase),实时 OLAP(Druid) 等数个技术产品,欢迎感兴趣的小伙伴联系.