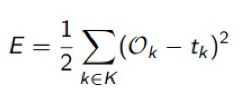对于现在流行的深度学习,保持学习精神是必要的――程序员尤其是架构师永远都要对核心技术和关键算法保持关注和敏感,必要时要动手写一写掌握下来,先不用关心什么时候用到――用不用是政治问题,会不会写是技术问题,就像军人不关心打不打的问题,而要关心如何打赢的问题。
程序员如何学习机器学习
对程序员来说,机器学习是有一定门槛的(这个门槛也是其核心竞争力),相信很多人在学习机器学习时都会为满是数学公式的英文论文而头疼,甚至可能知难而退。但实际上机器学习算法落地程序并不难写,下面是70行代码实现的反向多层(BP)神经网络算法,也就是深度学习。其实不光是神经网络,逻辑回归、决策树C45/ID3、随机森林、贝叶斯、协同过滤、图计算、Kmeans、PageRank等大部分机器学习算法都能在100行单机程序内实现(以后考虑分享出来)。
机器学习的真正难度在于它为什么要这么计算,它背后的数学原理是什么,怎么推导得来的公式,网上大部分的资料都在介绍这部分理论知识,却很少告诉你该算法的计算过程和程序落地是怎么样的,对于程序员来说,你需要做的仅是工程化应用,而不需要证明出一项新的数学计算方法。实际大部分机器学习工程师都是利用别人写好的开源包或者工具软件,输入数据和调整计算系数来训练结果,甚至很少自己实现算法过程。但是掌握每个算法的计算过程仍然非常重要,这样你才能理解该算法让数据产生了什么样的变化,理解算法的目的是为了达到什么样的效果。
本文重点探讨反向神经网络的单机实现,关于神经网络的多机并行化, Fourinone 提供非常灵活完善的并行计算框架,我们只需要理解透单机程序实现,就能构思和设计出分布式并行化方案,如果不理解算法计算过程,一切思路将无法展开。另外,还有卷积神经网络,主要是一种降维思想,用于图像处理,不在本文讨论范围。
神经网络过程描述:
首先,要明确,神经网络做的是预测任务,相信你记得高中学过的最小二乘法,我们可以以此做一个不严谨但比较直观的类比:
首先,我们要得到一个数据集和数据集的标记(最小二乘法中,我们也得到了一组组x,y的值)
算法根据这个数据集和对应的标记,拟合一个能够表达这个数据集的函数参数(也就是最小二乘法中计算a, b的公式,神经网络中不过是这个公式没法直接得到)
我们以此得到了拟合的函数(也就是最小二乘法中的拟合直线y^=ax+b)
接下来,带入新的数据之后,就可以生成对应的预测值y^(在最小二乘法中,就是带入y^=ax+b得到我们预测的y^,神经网络算法也是的,只不过求得的函数比最小二乘法复杂得多)。
神经网络的计算过程
神经网络结构如下图所示,最左边的是输入层,最右边的是输出层,中间是多个隐含层,隐含层和输出层的每个神经节点,都是由上一层节点乘以其权重累加得到,标上“+1”的圆圈为截距项b,对输入层外每个节点:Y=w0*x0+w1*x1+…+wn*xn+b,由此我们可以知道神经网络相当于一个多层逻辑回归的结构。
算法计算过程:输入层开始,从左往右计算,逐层往前直到输出层产生结果。如果结果值和目标值有差距,再从右往左算,逐层向后计算每个节点的误差,并且调整每个节点的所有权重,反向到达输入层后,又重新向前计算,重复迭代以上步骤,直到所有权重参数收敛到一个合理值。由于计算机程序求解方程参数和数学求法不一样,一般是先随机选取参数,然后不断调整参数减少误差直到逼近正确值,所以大部分的机器学习都是在不断迭代训练,下面我们从程序上详细看看该过程实现就清楚了。
神经网络的算法程序实现
神经网络的算法程序实现分为初始化、向前计算结果,反向修改权重三个过程。
1. 初始化过程
由于是n层神经网络,我们用二维数组layer记录节点值,第一维为层数,第二维为该层节点位置,数组的值为节点值;同样,节点误差值layerErr也是相似方式记录。用三维数组layer_weight记录各节点权重,第一维为层数,第二维为该层节点位置,第三维为下层节点位置,数组的值为某节点到达下层某节点的权重值,初始值为0-1之间的随机数。为了优化收敛速度,这里采用动量法权值调整,需要记录上一次权值调整量,用三维数组layer_weight_delta来记录,截距项处理:程序里将截距的值设置为1,这样只需要计算它的权重就可以了,
2. 向前计算结果
采用S函数1/(1+Math.exp(-z))将每个节点的值统一到0-1之间,再逐层向前计算直到输出层,对于输出层,实际上是不需要再用S函数的,我们这里将输出结果视为0到1之间的概率值,所以也采用了S函数,这样也有利于程序实现的统一性。
3. 反向修改权重
神经网络如何计算误差,一般采用平方型误差函数E,如下:
也就是将多个输出项和对应目标值的误差的平方累加起来,再除以2。实际上逻辑回归的误差函数也是这个,至于为什么要用这个函数来计算误差,它从数学上的合理性是什么,怎么得来的,这个我建议程序员们不想当数学家的话,先不去深究了,现在我们要做的是如何把这个函数E误差取它的最小值,需要对其进行求导,如果有些求导数学基础的话,倒可以尝试去推导下如何从函数E对权重求导得到下面这个公式的:
不会推导也没有关系,我们只需要运用结果公式就可以了,在我们的程序里用layerErr记录了E对权重求导后的最小化误差,再根据最小化误差去调整权重。
注意这里采用动量法调整,将上一次调整的经验考虑进来,避免陷入局部最小值,下面的k代表迭代次数,mobp为动量项,rate为学习步长:
Δw(k+1) = mobp*Δw(k)+rate*Err*Layer
也有很多使用下面的公式,效果上的差别不是太大:
Δw(k+1) = mobp*Δw(k)+(1-mobp)rate*Err*Layer
为了提升性能,注意程序实现是在一个while里面同时计算误差和调整权重,先将位置定位到倒数第二层(也就是最后一层隐含层)上,然后逐层反向调整,根据L+1层算好的误差来调整L层的权重,同时计算好L层的误差,用于下一次循环到L-1层时计算权重,以此循环下去直到倒数第一层(输入层)结束。
小结
在整个计算过程中,节点的值是每次计算都在变化的,不需要保存,而权重参数和误差参数是需要保存的,需要为下一次迭代提供支持,因此,如果我们构思一个分布式的多机并行计算方案,就能理解其他框架中为什么会有一个Parameter Server的概念。
多层神经网络完整程序实现
下面的实现程序BpDeep.java可以直接拿去使用,也很容易修改为C、C#、Python等其他任何语言实现,因为都是使用的基本语句,没有用到其他Java库(除了Random函数)。
import java.util.Random;
public class BpDeep{
public double[][] layer;//神经网络各层节点
public double[][] layerErr;//神经网络各节点误差
public double[][][] layer_weight;//各层节点权重
public double[][][] layer_weight_delta;//各层节点权重动量
public double mobp;//动量系数
public double rate;//学习系数
public BpDeep(int[] layernum, double rate, double mobp){
this.mobp = mobp;
this.rate = rate;
layer = new double[layernum.length][];
layerErr = new double[layernum.length][];
layer_weight = new double[layernum.length][][];
layer_weight_delta = new double[layernum.length][][];
Random random = new Random();
for(int l=0;l0){
for(int j=0;j0?layerErr[l+1][i]*layer_weight[l][j][i]:0;
layer_weight_delta[l][j][i]= mobp*layer_weight_delta[l][j][i]+rate*layerErr[l+1][i]*layer[l][j];//隐含层动量调整
layer_weight[l][j][i]+=layer_weight_delta[l][j][i];//隐含层权重调整
if(j==layerErr[l].length-1){
layer_weight_delta[l][j+1][i]= mobp*layer_weight_delta[l][j+1][i]+rate*layerErr[l+1][i];//截距动量调整
layer_weight[l][j+1][i]+=layer_weight_delta[l][j+1][i];//截距权重调整
}
}
layerErr[l][j]=z*layer[l][j]*(1-layer[l][j]);//记录误差
}
}
}
public void train(double[] in, double[] tar){
double[] out = computeOut(in);
updateWeight(tar);
}
}
一个运用神经网络的例子
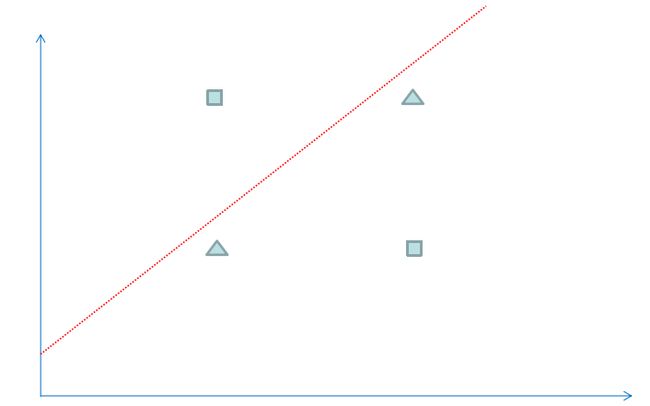
最后我们找个简单例子来看看神经网络神奇的效果。为了方便观察数据分布,我们选用一个二维坐标的数据,下面共有4个数据,方块代表数据的类型为1,三角代表数据的类型为0,可以看到属于方块类型的数据有(1,2)和(2,1),属于三角类型的数据有(1,1),(2,2),现在问题是需要在平面上将4个数据分成1和0两类,并以此来预测新的数据的类型。
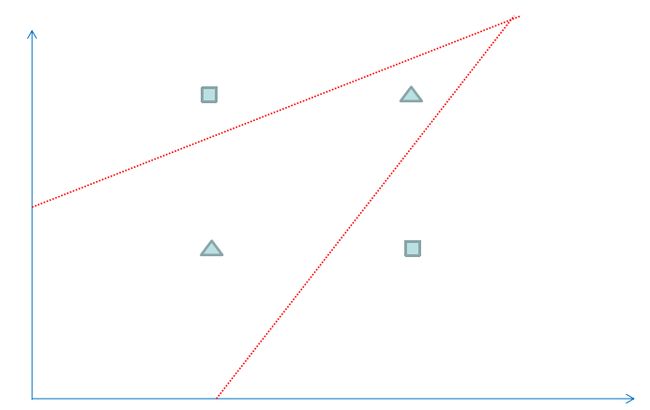
我们可以运用逻辑回归算法来解决上面的分类问题,但是逻辑回归得到一个线性的直线做为分界线,可以看到上面的红线无论怎么摆放,总是有一个样本被错误地划分到不同类型中,所以对于上面的数据,仅仅一条直线不能很正确地划分他们的分类,如果我们运用神经网络算法,可以得到下图的分类效果,相当于多条直线求并集来划分空间,这样准确性更高。
下面是这个测试程序BpDeepTest.java的源码:
import java.util.Arrays;
public class BpDeepTest{
public static void main(String[] args){
//初始化神经网络的基本配置
//第一个参数是一个整型数组,表示神经网络的层数和每层节点数,比如{3,10,10,10,10,2}表示输入层是3个节点,输出层是2个节点,中间有4层隐含层,每层10个节点
//第二个参数是学习步长,第三个参数是动量系数
BpDeep bp = new BpDeep(new int[]{2,10,2}, 0.15, 0.8);
//设置样本数据,对应上面的4个二维坐标数据
double[][] data = new double[][]{{1,2},{2,2},{1,1},{2,1}};
//设置目标数据,对应4个坐标数据的分类
double[][] target = new double[][]{{1,0},{0,1},{0,1},{1,0}};
//迭代训练5000次
for(int n=0;n<5000;n++)
for(int i=0;i
小结
以上测试程序显示神经网络有很神奇的分类效果,实际上神经网络有一定优势,但也不是接近人脑的万能算法,很多时候它可能会让我们失望,还需要结合各种场景的数据大量运用去观察其效果。我们可以把1层隐含层改成n层,并调整每层节点数、迭代次数、学习步长和动量系数,以获得一个最优化的结果。但是很多时候n层隐含层的效果并不比1层有明显提升,反而计算更复杂耗时,我们对神经网络的认识还需要多实践多体会。
以上就是本文关于70行Java代码实现深度神经网络算法分享的全部内容,希望对大家有所帮助。如有不足之处,欢迎留言指出。