引言
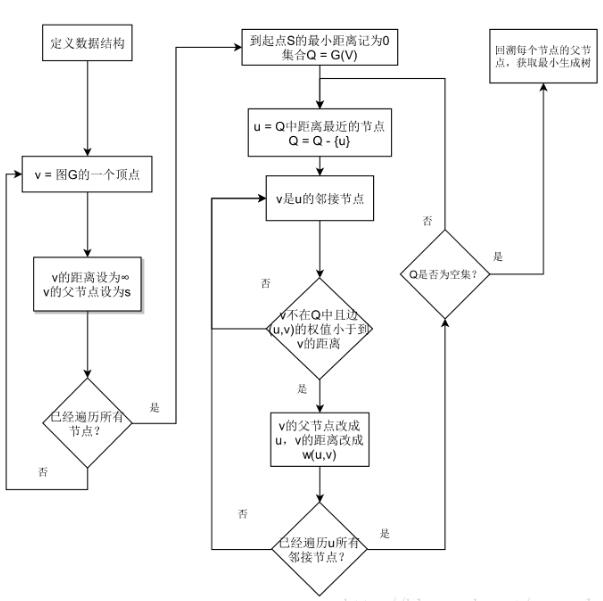
Prim算法与Dijkstra的最短路径算法类似,它采用贪心策略。算法开始先把图中权值最小的边添加到树T中,然后不断把权值最小的边E(E的一个端点在T中,另一个在G-T中)。当没有符合条件的E时算法结束,此时T就是G的一个最小生成树。
NetworkX是一款Python的软件包,用于创造、操作复杂网络,以及学习复杂网络的结构、动力学及其功能。 本文借助networkx.Graph类实现Prim算法。
正文
Prim算法的代码
Prim
def prim(G, s):
dist = {} # dist记录到节点的最小距离
parent = {} # parent记录最小生成树的双亲表
Q = list(G.nodes()) # Q包含所有未被生成树覆盖的节点
MAXDIST = 9999.99 # MAXDIST表示正无穷,即两节点不邻接
# 初始化数据
# 所有节点的最小距离设为MAXDIST,父节点设为None
for v in G.nodes():
dist[v] = MAXDIST
parent[v] = None
# 到开始节点s的距离设为0
dist[s] = 0
# 不断从Q中取出“最近”的节点加入最小生成树
# 当Q为空时停止循环,算法结束
while Q:
# 取出“最近”的节点u,把u加入最小生成树
u = Q[0]
for v in Q:
if (dist[v] < dist[u]):
u = v
Q.remove(u)
# 更新u的邻接节点的最小距离
for v in G.adj[u]:
if (v in Q) and (G[u][v]['weight'] < dist[v]):
parent[v] = u
dist[v] = G[u][v]['weight']
# 算法结束,以双亲表的形式返回最小生成树
return parent
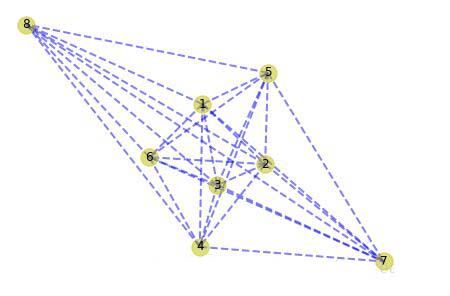
测试数据
| 从~到 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 1 | 1.3 | 2.1 | 0.9 | 0.7 | 1.8 | 2.0 | 1.8 |
| 2 | 0.9 | 1.8 | 1.2 | 2.8 | 2.3 | 1.1 | |
| 3 | 2.6 | 1.7 | 2.5 | 1.9 | 1.0 | ||
| 4 | 0.7 | 1.6 | 1.5 | 0.9 | |||
| 5 | 0.9 | 1.1 | 0.8 | ||||
| 6 | 0.6 | 1.0 | |||||
| 7 | 0.5 |
测试代码
import matplotlib.pyplot as plt import networkx as nx g_data = [(1, 2, 1.3), (1, 3, 2.1), (1, 4, 0.9), (1, 5, 0.7), (1, 6, 1.8), (1, 7, 2.0), (1, 8, 1.8), (2, 3, 0.9), (2, 4, 1.8), (2, 5, 1.2), (2, 6, 2.8), (2, 7, 2.3), (2, 8, 1.1), (3, 4, 2.6), (3, 5, 1.7), (3, 6, 2.5), (3, 7, 1.9), (3, 8, 1.0), (4, 5, 0.7), (4, 6, 1.6), (4, 7, 1.5), (4, 8, 0.9), (5, 6, 0.9), (5, 7, 1.1), (5, 8, 0.8), (6, 7, 0.6), (6, 8, 1.0), (7, 8, 0.5)] def draw(g): pos = nx.spring_layout(g) nx.draw(g, pos, \ arrows=True, \ with_labels=True, \ nodelist=g.nodes(), \ style='dashed', \ edge_color='b', \ width=2, \ node_color='y', \ alpha=0.5) plt.show() g = nx.Graph() g.add_weighted_edges_from(g_data) tree = prim(g, 1) mtg = nx.Graph() mtg.add_edges_from(tree.items()) mtg.remove_node(None) draw(mtg)
运行结果
以上这篇NetworkX之Prim算法(实例讲解)就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。