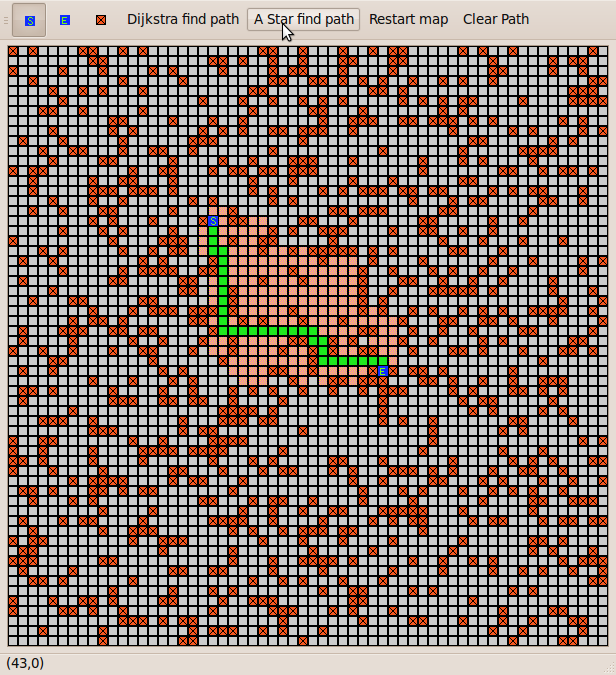
紧接上一篇《Unity NavMesh寻路 & A* (A star)分析及实例应用(一)》,本文重点讲解A* 算法在Unity中的寻路实现(当然寻路算法不止 A* 这一种, 还有递归, 非递归, 广度优先, 深度优先, 使用堆栈等等, 有兴趣的可以研究研究~~),文尾会将本人GitHub上的实例Demo共享出来方便大家参考,有精力深挖的同学可以根据下文继续探索:http://www.redblobgames.com/pathfinding/a-star/introduction.html
原理:
AStar 使用 F = G + H 来评估一个节点。其中 G 代表起始节点到这个节点的代价,H 代表目的节点到这个节点的代价。这样,从起始节点开始,不断的寻找邻居节点中 F 最小的,直到检测到目的节点从而找到路径为止。
A*算法(A-star)其实是一种启发式搜索或者说成是在状态空间中的搜索,首先对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
启发中的估价是用估价函数表示的,如:f(n) = g(n) + h(n)
其中f(n) 是节点n的估价函数,g(n)是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。如果说详细点,g(n)代表了搜索的广度的优先趋势。但是当h(n) >> g(n)时,可以省略g(n),而提高效率
这里有公式f
最终路径长度f = 起点到该点的已知长度h + 该点到终点的估计长度g。
O表(open):
待处理的节点表。
C表(close):
已处理过的节点表。
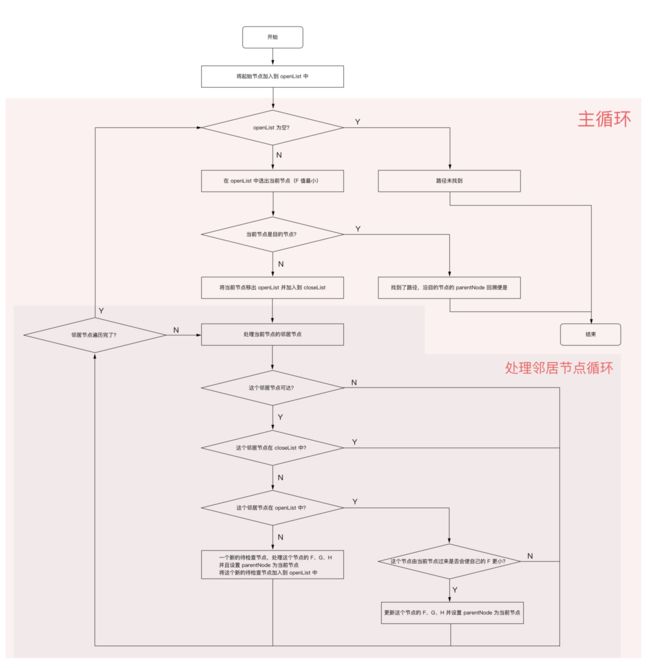
下面是算法流程图:
AStar 维护着一个开放列表和一个封闭列表。开放列表中存放着待检查 F 值的节点,每次主循环中都从 openList 中寻找 F 值最小的节点作为当前节点,然后将当前节点的邻居节点加入到 openList 中作为待检查节点。封闭列表存放着不再检查的节点,每当选出一个当前节点之后意味着它的邻居节点将要或已经加入到开放列表中,这个当前节点便成为了一个不再检查的节点,所以要把它加入到 closeList 中,防止再次检查。
在邻居节点循环中如果这个邻居节点不在 openList 中,那就需要设置 F、G、H 和 parentNode 并加入到 openList 中备选。
在邻居节点循环中如果这个节点已经在 openList 中,说明它之前已经作为邻居节点加入到了 openList 中,但是没有被选为当前节点(因为它的 F 不是最小的)。而此时它又成为了另一个节点的邻居节点,如果经由当前节点到这个节点的 F 值变小了那就更新这个邻居节点的数据,否则什么也不做。
openList 为空说明搜索了所有地图而没有找到路径。
当前节点为目的节点说明路径已经找到,沿着当前节点的 parentNode 回溯就可以得到路径数据。
G 和 H
AStar 依据 G 和 H 值来评估一个节点在本次寻路过程中的代价。
这两个值将经由这个节点的路径的代价分割成两部分:
一部分是由起始节点到这个节点的代价 G ,因为路径的搜索过程是从起始节点开始循环的检查当前节点的每个邻居节点,所以这个值是确定的。
另一部分 F 是这个节点到目的节点的代价,这个值一般是一个估计值(也可以是精确的)。这样,因为有 H 值影响着 F 的大小,路径的搜索会有一个大概的方向,即 H 值会不断的把搜索方向导向目的节点的方向,这也是为什么 AStar 会更快,因为 H 值减少了算法检查的节点个数。
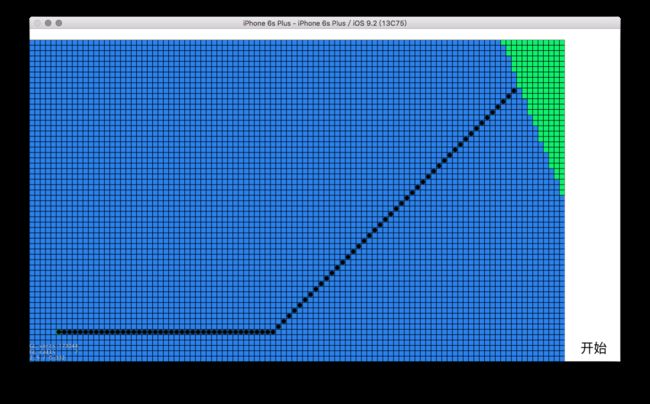
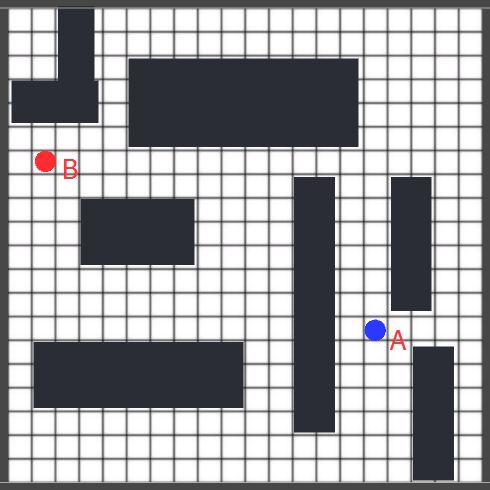
下面用几张截图来说明这两个值的作用。如下图,现在有这样一个地图,先不考虑地图中有其它山啊水啊不可达的区域,假设地图上任何一个节点都是可达的,现在要在两个圆点标记的节点中寻找一条路径。
屏幕快照 2016-02-19 22.09.32.png
首先是使用了“曼哈顿”方法计算 H 值的 AStar 结果,图中蓝色的节点是算法过程中被加入到了 openList 中的节点,可以看到这个搜索过程没有检查过多的节点,从一开始就向着目的节点的方向搜索过去。
下面,把每个 H 值的节点都置 0,也就是说完全消除 H 值对算法的影响,根据原理大概可以预测到搜索过程会以起始节点为圆心,不断的向外扩展,直到到达了目的节点为止。下面是截图:
G 让算法找到更好的路径,而 H 让算法更快的找到路径。
G 和 H 的单位问题
因为 F 是由 G 和 H 相加得来的,所以二者的度量应该是统一的。如果二者的度量不统一就会使二者中的一个值在节点评估中起主导作用,而另一个值变得失效了。比如再看使用了“曼哈顿”方法计算 H 值的 AStar ,这次把 H 值缩小十倍,算法检查了更多的节点,从而速度会变慢。
计算 H 的几种常用方法
精确的 H 值
可以在路径搜索之前预先计算任意两个节点之间的代价,然后在计算 H 值的时候直接查找这个值。但是这个方法在实际中不太现实,因为在大多数游戏中一般地图比较大、节点多(预计算的数据会很多)、存在着未知区域(无法预先计算)、地图上还存在着其它的移动目标。这些因素都会使得这种精确 H 值的方法不是那么容易实现。
近似精确的 H 值
在地图上均匀的设置一些导航点,预先计算任意两个导航点的代价。寻路过程中,当要计算 H 值的时候,先寻找距离当前节点最近的导航点 w1 和距离目的节点最近的导航点 w2 ,这样 H 值就变成了一下这种形式:
H = h(当前节点, w1) + h(目的节点, w2) + distance(w1, w2)
曼哈顿方法
设当前节点: n(column, row) ,目的节点 t(column, row)
HManhattan(n) = D * [abs(n.column - t.column) + abs(n.row - t.row)]
(其中 D 是为了平衡 G 和 H 的度量)
对角线方法
设当前节点: n(column, row) ,目的节点 t(column, row)
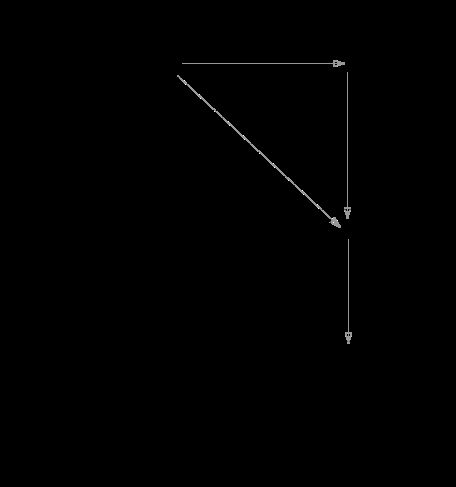
如上图,路径可以先沿对角线方向走向中间节点 x,再沿直线走向目的节点 t。首先,对角线的代价为
Hd = Dd * [min(abs(n.column - t.column), abs(n.row - c.row))]
直线的代价为:
Hs = Ds * [max(abs(n.column - t.column), abs(n.row - c.row)) - min(abs(n.column - t.column), abs(n.row - c.row))]
H = Hd + Hs
欧几里得和平方欧几里德方法
设当前节点: n(column, row) ,目的节点 t(column, row)
H = D * sqrt((n.column - t.column)(n.column - t.column) + (n.row - t.row)(n.row - t.row))
计算机计算平方根比较耗时间,考虑把开平方的过程去掉,但是这样会导致 G 和 H 的度量不同。
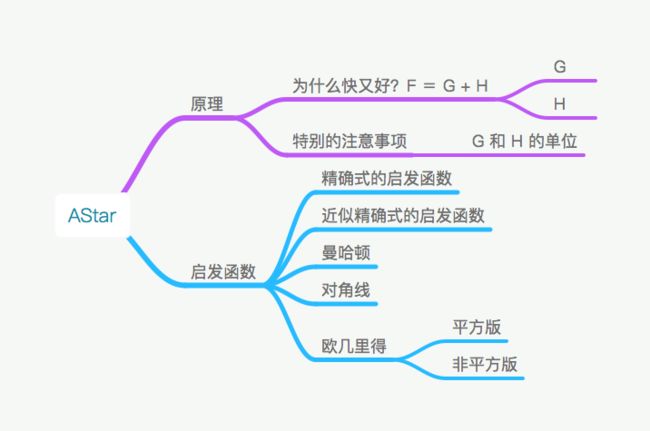
以上就是 AStar 的一些基本概念,最后来一个思维导图吧:
算法流程:
- 从起点开始,起点的f = 1 + g, 1表示此节点已走过的路径是1,g是此节点到终点的估计距离, 放入链表O中。
可以假设g值的计算使用勾股定理公式来计算此点到终点的直线距离。
- 当O不为空时,从中取出一个最小f值的节点x。
3.如果x等于终点,找到路径,算法结束。否则走第4步.
- 遍历x的所有相邻点,对所有相邻点使用公式f,计算出f值后,
先检查每个相邻节点y是否在链表O和C中,
如果在O中的话的话,更新y节点的f值,保留最小的f值,
如果在C中的话,并且此时f值比C中的f值小,则更新f值,将y节点从C中移到O中。否则不做操作。
如果不在以上两表中,按最小顺序排序将y插入链表O。最后将x插入C表中。
例如:
起点是 (1,1), 终点是(5,5), 取一个相邻点(0,1), 这时这个点的h=1+1 = 2, g可以用勾股定理公式来计算此点到终点的直线距离,就是 (5-0)*(5-0) - (5-1) *(5-1) = 9, 再开平方等于3,这样f就等于2+3 = 5.然后将此点插入链表O中。
如果相邻点不是路径,比如是障碍,那就跳过。
5.继续2,3,4步直到找到终点, 或者直到O为空表示没找到路径。
上面检查O和C表的原因是:
如果图是一个不规则的图,比如一个游戏里,有几个传送门,这样同一个点如果经过传送门的话,路径会大大缩短,这样就需要检查O和C表来更新f值,如果是一个不包含捷径(传送门)的图,那样就可以用个数组来标记已访问过的节点,这样就可以不用C表,也不用检查O表来更新f值。
对于没找到路径的结果,访问的节点有可能差不多是所有节点,这样的效率和Dijkstra一样低,我们可以使用同时从两端用A算法来找路径,这样当其中一个没找到路径的话,寻找结束。这样用的时间将是2 * min(S,E)的时间,S是从起点开始寻路径的时间,E是从终点开始寻路径的时间。这样的一个典型的例子是
终点是个孤立的点,没有任何点能到达他,而其他点都是链接的,那么如果光从起点开始找的话,要到访问完所有除终点之外的点后才知道找不到终点。这样的效率非常差。 如果同时从两端开始找,马上就能知道终点没有任何路径相邻,寻找结束。
在游戏中,有一个很常见地需求,就是要让一个角色从A点走向B点,我们期望是让角色走最少的路。嗯,大家可能会说,直线就是最短的。没错,但大多数时候,A到B中间都会出现一些角色无法穿越的东西,比如墙、坑等障碍物。这个时候怎么办呢? 是的,我们需要有一个算法来解决这个问题,算法的目标就是计算出两点之间的最短路径,而且要能避开障碍物。
简化搜索区域
要实现寻路,第一步我们要把场景简化出一个易于控制的搜索区域。
怎么处理要根据游戏来决定了。例如,我们可以将搜索区域划分成像素点,但是这样的划分粒度对于一般的游戏来说太高了(没必要)。
作为代替,我们使用格子(一个正方形)作为寻路算法的单元。其他的形状类型也是可能的(比如三角形或者六边形),但是正方形是最简单并且最常用的。
比如地图的长是w=2000像索,宽是h=2000像索,那么我们这个搜索区域可以是二维数组 map[w, h], 包含有400000个正方形,这实在太多了,而且很多时候地图还会更大。
现在让我们基于目前的区域,把区域划分成多个格子来代表搜索空间(在这个简单的例子中,20*20个格子 = 400 个格子, 每个格式代表了100像索):
既然我们创建了一个简单的搜索区域,我们来讨论下A星算法的工作原理吧。我们需要两个列表 (Open和Closed列表):
一个记录下所有被考虑来寻找最短路径的格子(称为open 列表)
一个记录下不会再被考虑的格子(成为closed列表)
首先在closed列表中添加当前位置(我们把这个开始点称为点 “A”)。然后,把所有与它当前位置相邻的可通行格子添加到open列表中。
现在我们要从A出发到B点。
在寻路过程中,角色总是不停从一个格子移动到另一个相邻的格子,如果单纯从距离上讲,移动到与自身斜对角的格子走的距离要长一些,而移动到与自身水平或垂直方面平行的格子,则要近一些。
为了描述这种区别,先引入二个概念:
节点(Node):每个格子都可以称为节点。
代价(Cost):描述角色移动到某个节点时所走的距离(或难易程度)。
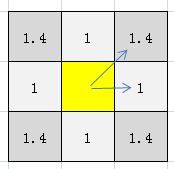
如上图,如果每水平或垂直方向移动相邻一个节点所花的代价记为1,则相邻对角节点的代码为1.4(即2的平方根--勾股定理)
通常寻路过程中的代价用f,g,h来表示
g代表(从指定节点到相邻)节点本身的代价--即上图中的1或1.4
h代表从指定节点到目标节点(根据不同的估价公式--后面会解释估价公式)估算出来的代价。
而 f = g + h 表示节点的总代价
///
/// 寻路节点
///
public class NodeItem {
// 是否是障碍物
public bool isWall;
// 位置
public Vector3 pos;
// 格子坐标
public int x, y;
// 与起点的长度
public int gCost;
// 与目标点的长度
public int hCost;
// 总的路径长度
public int fCost {
get {return gCost + hCost; }
}
// 父节点
public NodeItem parent;
public NodeItem(bool isWall, Vector3 pos, int x, int y) {
this.isWall = isWall;
this.pos = pos;
this.x = x;
this.y = y;
}
}
注意:这里有二个新的东东 isWall 和 parent。
通常障碍物本身也可以看成是由若干个不可通过的节点所组成,所以 isWall 是用来标记该节点是否为障碍物(节点)。
另外:在考查从一个节点移动到另一个节点时,总是拿自身节点周围的8个相邻节点来说事儿,相对于周边的节点来讲,自身节点称为它们的父节点(parent).
前面一直在提“网格,网格”,干脆把它也封装成类Grid.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
public class Grid : MonoBehaviour {
public GameObject NodeWall;
public GameObject Node;
// 节点半径
public float NodeRadius = 0.5f;
// 过滤墙体所在的层
public LayerMask WhatLayer;
// 玩家
public Transform player;
// 目标
public Transform destPos;
///
/// 寻路节点
///
public class NodeItem {
// 是否是障碍物
public bool isWall;
// 位置
public Vector3 pos;
// 格子坐标
public int x, y;
// 与起点的长度
public int gCost;
// 与目标点的长度
public int hCost;
// 总的路径长度
public int fCost {
get {return gCost + hCost; }
}
// 父节点
public NodeItem parent;
public NodeItem(bool isWall, Vector3 pos, int x, int y) {
this.isWall = isWall;
this.pos = pos;
this.x = x;
this.y = y;
}
}
private NodeItem[,] grid;
private int w, h;
private GameObject WallRange, PathRange;
private List pathObj = new List ();
void Awake() {
// 初始化格子
w = Mathf.RoundToInt(transform.localScale.x * 2);
h = Mathf.RoundToInt(transform.localScale.y * 2);
grid = new NodeItem[w, h];
WallRange = new GameObject ("WallRange");
PathRange = new GameObject ("PathRange");
// 将墙的信息写入格子中
for (int x = 0; x < w; x++) {
for (int y = 0; y < h; y++) {
Vector3 pos = new Vector3 (x*0.5f, y*0.5f, -0.25f);
// 通过节点中心发射圆形射线,检测当前位置是否可以行走
bool isWall = Physics.CheckSphere (pos, NodeRadius, WhatLayer);
// 构建一个节点
grid[x, y] = new NodeItem (isWall, pos, x, y);
// 如果是墙体,则画出不可行走的区域
if (isWall) {
GameObject obj = GameObject.Instantiate (NodeWall, pos, Quaternion.identity) as GameObject;
obj.transform.SetParent (WallRange.transform);
}
}
}
}
// 根据坐标获得一个节点
public NodeItem getItem(Vector3 position) {
int x = Mathf.RoundToInt (position.x) * 2;
int y = Mathf.RoundToInt (position.y) * 2;
x = Mathf.Clamp (x, 0, w - 1);
y = Mathf.Clamp (y, 0, h - 1);
return grid [x, y];
}
// 取得周围的节点
public List getNeibourhood(NodeItem node) {
List list = new List ();
for (int i = -1; i <= 1; i++) {
for (int j = -1; j <= 1; j++) {
// 如果是自己,则跳过
if (i == 0 && j == 0)
continue;
int x = node.x + i;
int y = node.y + j;
// 判断是否越界,如果没有,加到列表中
if (x < w && x >= 0 && y < h && y >= 0)
list.Add (grid [x, y]);
}
}
return list;
}
// 更新路径
public void updatePath(List lines) {
int curListSize = pathObj.Count;
for (int i = 0, max = lines.Count; i < max; i++) {
if (i < curListSize) {
pathObj [i].transform.position = lines [i].pos;
pathObj [i].SetActive (true);
} else {
GameObject obj = GameObject.Instantiate (Node, lines [i].pos, Quaternion.identity) as GameObject;
obj.transform.SetParent (PathRange.transform);
pathObj.Add (obj);
}
}
for (int i = lines.Count; i < curListSize; i++) {
pathObj [i].SetActive (false);
}
}
}
在寻路的过程中“条条道路通罗马”,路径通常不止一条,只不过所花的代价不同而已。
所以我们要做的事情,就是要尽最大努力找一条代价最小的路径。
但是,即使是代价相同的最佳路径,也有可能出现不同的走法。
用代码如何估算起点与终点之间的代价呢?
//曼哈顿估价法
private function manhattan(node:Node):Number
{
return Math.abs(node.x - _endNode.x) * _straightCost + Math.abs(node.y + _endNode.y) * _straightCost;
}
//几何估价法
private function euclidian(node:Node):Number
{
var dx:Number=node.x - _endNode.x;
var dy:Number=node.y - _endNode.y;
return Math.sqrt(dx * dx + dy * dy) * _straightCost;
}
//对角线估价法
private function diagonal(node:Node):Number
{
var dx:Number=Math.abs(node.x - _endNode.x);
var dy:Number=Math.abs(node.y - _endNode.y);
var diag:Number=Math.min(dx, dy);
var straight:Number=dx + dy;
return _diagCost * diag + _straightCost * (straight - 2 * diag);
}
上面的代码给出了三种基本的估价算法(也称估价公式),其算法示意图如下:
如上图,对于“曼哈顿算法”最贴切的描述莫过于孙燕姿唱过的那首成名曲“直来直往”,笔直的走,然后转个弯,再笔直的继续。
“几何算法”的最好解释就是“勾股定理”,算出起点与终点之间的直线距离,然后乘上代价因子。
“对角算法”综合了以上二种算法,先按对角线走,一直走到与终点水平或垂直平行后,再笔直的走。
这三种算法可以实现不同的寻路结果,我们这个例子用的是“对角算法”:
// 获取两个节点之间的距离
int getDistanceNodes(Grid.NodeItem a, Grid.NodeItem b) {
int cntX = Mathf.Abs (a.x - b.x);
int cntY = Mathf.Abs (a.y - b.y);
// 判断到底是那个轴相差的距离更远 , 实际上,为了简化计算,我们将代价*10变成了整数。
if (cntX > cntY) {
return 14 * cntY + 10 * (cntX - cntY);
} else {
return 14 * cntX + 10 * (cntY - cntX);
}
}
好吧,下面直接贴出全部的寻路算法 FindPath.cs:
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
public class FindPath : MonoBehaviour {
private Grid grid;
// Use this for initialization
void Start () {
grid = GetComponent ();
}
// Update is called once per frame
void Update () {
FindingPath (grid.player.position, grid.destPos.position);
}
// A*寻路
void FindingPath(Vector3 s, Vector3 e) {
Grid.NodeItem startNode = grid.getItem (s);
Grid.NodeItem endNode = grid.getItem (e);
List openSet = new List ();
HashSet closeSet = new HashSet ();
openSet.Add (startNode);
while (openSet.Count > 0) {
Grid.NodeItem curNode = openSet [0];
for (int i = 0, max = openSet.Count; i < max; i++) {
if (openSet [i].fCost <= curNode.fCost &&
openSet [i].hCost < curNode.hCost) {
curNode = openSet [i];
}
}
openSet.Remove (curNode);
closeSet.Add (curNode);
// 找到的目标节点
if (curNode == endNode) {
generatePath (startNode, endNode);
return;
}
// 判断周围节点,选择一个最优的节点
foreach (var item in grid.getNeibourhood(curNode)) {
// 如果是墙或者已经在关闭列表中
if (item.isWall || closeSet.Contains (item))
continue;
// 计算当前相领节点现开始节点距离
int newCost = curNode.gCost + getDistanceNodes (curNode, item);
// 如果距离更小,或者原来不在开始列表中
if (newCost < item.gCost || !openSet.Contains (item)) {
// 更新与开始节点的距离
item.gCost = newCost;
// 更新与终点的距离
item.hCost = getDistanceNodes (item, endNode);
// 更新父节点为当前选定的节点
item.parent = curNode;
// 如果节点是新加入的,将它加入打开列表中
if (!openSet.Contains (item)) {
openSet.Add (item);
}
}
}
}
generatePath (startNode, null);
}
// 生成路径
void generatePath(Grid.NodeItem startNode, Grid.NodeItem endNode) {
List path = new List();
if (endNode != null) {
Grid.NodeItem temp = endNode;
while (temp != startNode) {
path.Add (temp);
temp = temp.parent;
}
// 反转路径
path.Reverse ();
}
// 更新路径
grid.updatePath(path);
}
// 获取两个节点之间的距离
int getDistanceNodes(Grid.NodeItem a, Grid.NodeItem b) {
int cntX = Mathf.Abs (a.x - b.x);
int cntY = Mathf.Abs (a.y - b.y);
// 判断到底是那个轴相差的距离更远
if (cntX > cntY) {
return 14 * cntY + 10 * (cntX - cntY);
} else {
return 14 * cntX + 10 * (cntY - cntX);
}
}
}
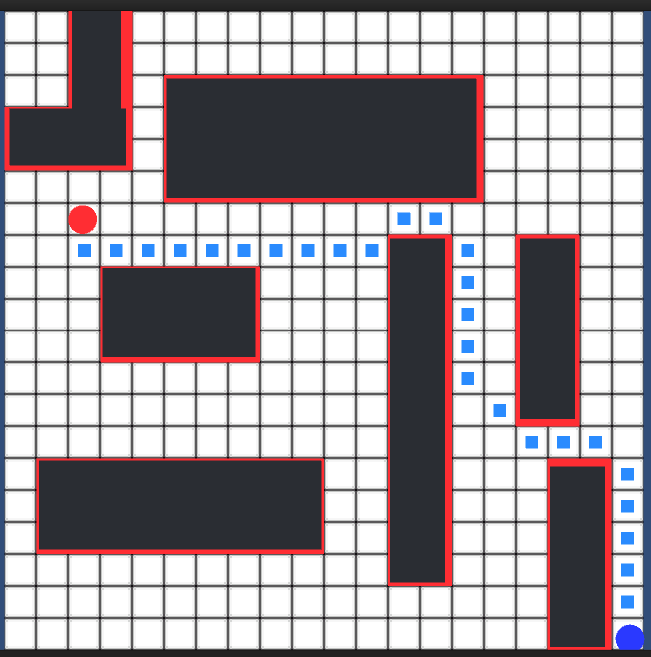
运行效果图:
红色区域是标识出来的不可以行走区域。(代码中对两个点的定位有点小小的问题,不过不影响算法的演示,自己下载修改一下)
完整代码下载:
https://git.oschina.net/lvlei_china/unity-aster.git