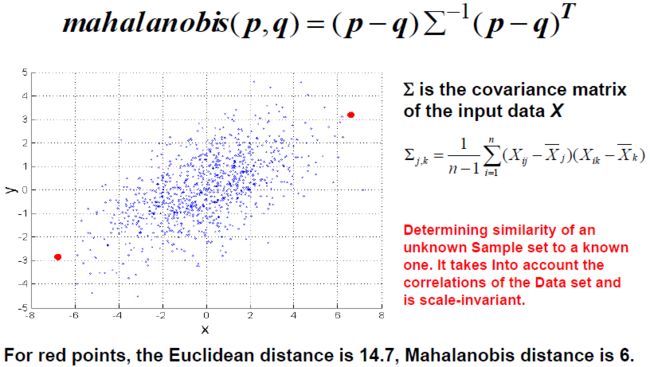
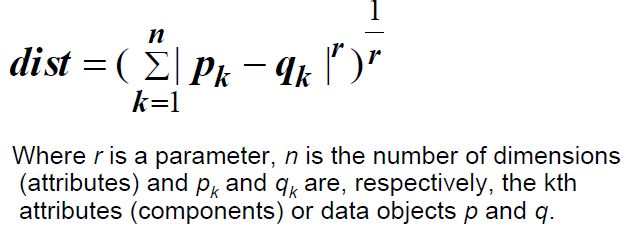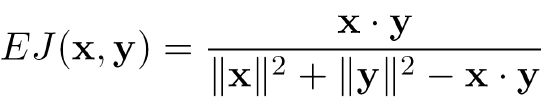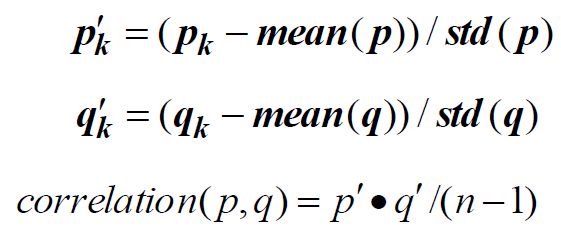- Python面向对象编程(OOP)详解:通俗易懂的全面指南
盛夏绽放
python开发语言有问必答
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。文章目录Python面向对象编程(OOP)详解:通俗易懂的全面指南一、OOP基本概念1.什么是面向对象编程?2.OOP的四大支柱3.核心概念对比表二、类和对象1.类(Class)vs对象(Object)2.类结构详解三、OOP三大特性详解1.封装(Encapsulation)2.继承(Inherita
- Python类中魔术方法(Magic Methods)完全指南:从入门到精通
盛夏绽放
python开发语言
文章目录Python类中魔术方法(MagicMethods)完全指南:从入门到精通一、魔术方法基础1.什么是魔术方法?2.魔术方法的特点二、常用魔术方法分类详解1.对象创建与初始化2.对象表示与字符串转换3.比较运算符重载4.算术运算符重载5.容器类型模拟6.上下文管理器7.可调用对象三、高级魔术方法1.属性访问控制2.描述符协议3.数值类型转换四、魔术方法最佳实践五、综合案例:自定义分数类Pyt
- 【中项第三版】系统集成项目管理工程师 | 第 7 章 软硬件系统集成
Jackilina_Stone
#系统集成项目管理工程师中项第3版软考中级
前言第7章对应的内容选择题和案例分析都可能会进行考查,学习要以教材为准。目录7.1系统集成基础7.2基础设施集成7.2.1弱电工程7.2.2网络集成1传输子系统2交换子系统3网管子系统4安全子系统5服务子系统7.2.3数据中心集成7.3软件集成7.3.1基础软件集成7.3.2应用软件集成7.3.3其他软件集成7.4业务应用集成7.5本章练习7.1系统集成基础软硬件系统集成是以信息的集成为目标,功能
- Vue3.0性能优化(v-memo指令)
Vue3.0v-memo指令性能优化Vue3.0的v-memo指令是一个强大的性能优化工具,尤其适用于渲染大量静态列表或复杂组件时。它通过缓存渲染结果来避免不必要的重新渲染,从而提升应用性能。基本用法v-memo接收一个依赖数组,只有当数组中的值发生变化时才会重新渲染:适用场景大型静态列表:当列表数据量大且不经常变化时{{product.name}}复杂组件嵌套:避免深层子组件的不必要更新条件渲染
- 《小狗钱钱》学习心得(第三、四、五章)
A01琪公子
《小狗钱钱》学习心得(第三、四、五章)最近在跟战友读一本《小狗钱钱》的书,今天把读到的精华与对这本书的感悟分享给正在看文章的你,希望对你有用。一、成功笔记:1.昨天的梦想相册的三个重要梦想开始在我脑海中浮现,我闭眼想到靠自己努力买房并装修好的新房的温馨舒适、爸妈安享晚年的幸福时刻,以及清晨爱人醒来那甜蜜的微笑。2.给客户重新发了合同,不在急急燥燥,而是准备好,只要有机会,就紧紧抓住。3.用心读完了
- 2019-7-17
yl柠檬草的味道
六项精进姓名:袁丽公司:上海缘缀包装材料有限公司【日精进打卡第353天】【知~学习】《六项精进》1遍共242遍《大学》1遍共242遍公司使命、愿景、价值观1遍共23遍【经典名句分享】【行~实践】一、修身:(对自己个人)1、步行:80002、坚持学习19天3、做早餐二、齐家:(对家庭和家人)1、和家人视频,都都快过来了,让她把要带过来的东西准备好,不错!小家伙能熟背我的手机号码了!三、建功:(对工作
- 2018-12-23
岳岳孙孙
起初,写30条觉得好多啊,有这么多感谢自己的吗?真正静下心来,回想2018年,各种小事历历在目,各种幸福和温馨。觉得自己真正的成为了一个有志青年。不仅仅对父母,对丈夫,对兄弟姐妹,对公司,对工作,更对自己。1.真的感觉卓越圈选择了我,没去卓越圈之前,觉得自己是个挺优秀的人,可是真正进入卓越圈,才发现什么样的才是优秀的人,像叶叶,亦轩,雨涵,甜甜,彬彬。。。。所有的人都有自己的闪光点。。。2.201
- 习题 4.2 输出最佳车的车号,以及哪位专家说对了
西蒙尼的马竞
c++算法开发语言
4名专家对4款赛车进行评论。A说:2号赛车是最好的。B说;4号赛车是最好的。C说:3号不是最佳赛,。D说:B说错了。事实上只有一款赛车最佳,且只有一名专家说对了,其他3人都说错了。请编程输出最佳车的车号,以及哪位专家说对了。//************************************************//*SourceName:ChapterFour_ExerciseTwo.
- 习题4.3 解出比赛的实际名次
西蒙尼的马竞
c++算法开发语言
5位跳水高手将参加10m高台跳水决赛,有好事者让5人据实力预测比赛结果。A选手说:B第二,我第三。B选手说:我第二,E第四。C选手说:我第一,D第二。D选手说:C最后,我第三。E选手说:我第四,A第一。决赛成绩公布之后,每位选手的预测都只说对了一半,即一对一错。请编程解出比赛的实际名次。//************************************************//*Sou
- 京东618红包怎么领取红包口令在哪里领取(京东618大额红包密令怎么领取方法)
全网优惠分享
2023年京东618红包将在5月29日开始发放,本文讲解2023年京东618红包领取方法,教大家怎么领取京东618红包!京东618元现金红包获取方法:京东618元红包领取地址:https://u.jd.com/as2ixNh(复制打开领取)618元红包口令:¥CEDHP3lrm2Geq82U¥复制打开京东APP即可领取或者打开京东APP扫一扫下面的二维码也可获取京东购物省钱秘籍分享(认真看完你就会
- 20190309易效能5.0践行第三周总结
小梨子_59bd
一、我的三个标签:1.两个孩子的母亲,父母的高度决定孩子的高度,不断学习,更好的陪伴,做孩子的榜样。2.财务工作者,目前在公司里负责财务管理工作。3.广东狮子会会员狮子会是一个公益慈善服务组织,出钱、出力、出心、出席,加入狮子会参加各项服务活动让我和我的家人更好的成长,收获更多的爱。让付出成为习惯。二、【90天大目标】(具体化,可衡量)1、运动:每周至少三次2、阅读:亲子阅读和自己阅读3、早睡22
- 〖Python 数据库开发实战 - Redis篇②〗- Linux系统下安装 Redis 数据库
哈哥撩编程
#⑤-数据库开发实战篇Python全栈白宝书python数据库数据库开发实战linux安装redis
订阅Python全栈白宝书-零基础入门篇可报销!白嫖入口-请点击我。推荐他人订阅,可获取扣除平台费用后的35%收益,文末名片加V!说明:该文属于Python全栈白宝书专栏,免费阶段订阅数量4300+,购买任意白宝书体系化专栏可加入TFS-CLUB私域社区。福利:加入社区的小伙伴们,除了可以获取博主所有付费专栏的阅读权限之外,还有机会加入星荐官共赢计划,详情请戳我。作者:不渴望力量的哈士奇(哈哥),
- 独行
熙琄细语雪
讲师四期蒋袁莉分享387天学习心理学,考证,选择焦点流派深入学习,二年多的时间,起初是独行,慢慢有了伙伴,有了团队,庆幸自己的坚持,庆幸内心的安稳与富足。游泳坚持三天了,独来独往,计算着行程时间,游泳时间,坚持着自己预定的游泳量,不去与他人比,享受着自己的进步,感受着周围的快乐,这个冬天我相信自己能坚持下来一周二三次的量,既为自己,也为孩子做个榜样:一个人,决定了的事,要坚持,在坚持中享受!
- 女生必看:独居的注意事项
上秋十一
1.换锁换锁啊,实在换不了某宝找封门器,顶门器。前房客作案的案例不要太多,最最关键的是现在的锁小偷都能打开,为了稳妥还是要买个封门器哦。2.租房用吸铁石检查有没有针孔摄像头,之前看过一个案例说是某些房东特地安装了针孔摄像头来偷懒女租客洗澡。现在连酒店都被不怀好意的人安装上了,民用的住房就更容易存在针孔摄像头啦!想想每天被人偷窥是不是很恐怖!!!!3.女生租房子,一定不能选择偏僻地点的房子。这个太重
- 5.8g微波雷达芯片_导弹、卫星、雷达的军用芯片龙头——亚光科技
小胖娃
5.8g微波雷达芯片
亚光电子(上市公司持股97.38%)是国内最大的微波半导体器件、微波电路军用企业之一,与中电科13所、55所同处国内军用微波组件第一梯队。亚光电子主要产品为半导体分立器件、芯片、微波电路及组件,应用于三大领域:雷达、导引头、航天通信(卫星等航天器)。从产业逻辑上来看,亚光电子与紫光国微同处高景气度的军用芯片赛道。亚光电子做军用模拟芯片,实现微波信号的接收与发射,亚光电子的产业也聚焦于收发处理环节;
- java语言程序设计基础篇课后答案第八版_Java语言程序设计-基础篇-第八版-复习题-第一章...
1.1计算机是一种电子装置,存储和处理数据。一台计算机包括硬件和软件。在一般情况下,硬件是可以看到的计算机的物理方面的,而软件是无形的指令,控制硬件和它的工作。1.2一台计算机的硬件包括一个CPU,高速缓存,内存,硬盘,软盘,显示器,打印机,通信设备。1.3机器语言是每个计算机中内置的一组基本指令。汇编语言是一种低级别的编程语言,是用一个助记符来表示各机器语言指令。高级程序设计语言是像英语那样的易
- python分布式爬虫打造搜索引擎--------scrapy实现
weixin_30515513
爬虫python开发工具
http://www.cnblogs.com/jinxiao-pu/p/6706319.html最近在网上学习一门关于scrapy爬虫的课程,觉得还不错,以下是目录还在更新中,我觉得有必要好好的做下笔记,研究研究。第1章课程介绍1-1python分布式爬虫打造搜索引擎简介07:23第2章windows下搭建开发环境2-1pycharm的安装和简单使用10:272-2mysql和navicat的安装
- 上传文件csv并解析list_基于PyQt5表格控件TableWidget的csv文件内容显示
(70后红太阳2020年4月写于成都)一、配置环境开发环境:Win7;开发工具:Python3.8.2IDLE,QtDesigner5.13.2;Python安装目录:D:python;文件保存目录:D:python基于PyQt5表格控件TableWidget的csv文件内容显示;路径配置:在cmd下,运行path=%path%;Dpythonpython38-32scripts;D:python
- 从0到1:Maven下载安装与配置全攻略
目录一、Maven是什么二、为什么需要Maven2.1依赖管理难题2.2构建过程的复杂性三、下载Maven3.1下载前准备3.2下载步骤四、安装Maven4.1解压安装包4.2移动Maven文件夹(可选,Linux适用)五、配置Maven5.1配置环境变量5.2验证安装5.3配置本地仓库5.4配置远程仓库(可选)六、总结一、Maven是什么Maven是一个跨平台的项目管理工具,主要服务于基于Jav
- 请你停下3秒:写作的捷径,肯定有
叶两步
文/叶老巫(2018年:12/365)本文关键词:捷径、多读、多写、特色【壹】人,是很懒的另类动物。凡事,在思维上,首先想的是,怎样快速到达目的地。在写作上,也是如此。写作水平,要有所提高,是有捷径走的。有一条捷径,你必须走,才能到达你梦想的地方。这条捷径,我说出来,你会失望的。唯一的捷径,就是必须多读,还要多写。【贰】你会睁大眼睛,看着我,心里一个大大的问号:为什么是这个呢?话说,多读多写,人人
- 《Java语言程序设计》(基础篇原书第10版)第一章复习题答案
第一章1.1:硬件包括计算机中可以看得见的物理部分,而软件提供看不见的指令,这些指令控制硬件并且使得硬件完成特定的任务。1.2:中央处理器(CPU)内存(主存)存储设备(例如,磁盘和光盘)输入设备(例如,鼠标和键盘)输出设备(例如,显示器和打印机)通信设备(例如,调制解调器和网卡)1.3:代表电脑中央处理器。1.4:速度衡量单位是赫兹,1赫兹相当于每秒一个脉冲。20世纪90年代计算机的时钟速度通常
- “解读《文化自信和民族复兴》”(54)“五个数字背后的启迪 之"心上用功的3.0企业家"
周安柱
客户不仅需要物质财富,更渴望精神财富。当企业家在提供产品和服务的过程中成就客户建设心灵品质,则他所从事的事业就与化育人心的事业相应。相对于在事上用功的企业家,1.0企业家在德上用功,2.0企业家在道上用功,3.0企业家在心上用功。3.0企业家培养3.0团队,制定3.0战略,打造3.0产品,不仅满足客户的物质需求,而且通过成就员工与客户建设心灵品质以满足其精神需求,极大提高利益员工与客户的价值,从而
- HTML的重要知识
萌新小白的逆袭
html前端
什么是HTMLHTML是HyperTextMarkupLanguage的缩写,意思是超文本标记语言。标签标题标签:————-h1,h2,h3.....段落标签:————p换行标签:————br列表标签:有序列表:——ol无序列表:——ul超链接标签:————href属性使用路径target用于定义链接打开的方式_blank在新窗口中打开目标资源;_self在当前窗口中打开目标资源多媒体标签:图片标
- 【家庭经济学】陈健
中流砥柱陈健
【家庭经济学专栏】陈健(356)林园6确定性卖出“老公,老公”朱姨渐渐地觉得,林园的投.资策略更接地气,一早起来,就煮水泡茶,听朱公吹水。朱公品了口茶,“老婆,林园的确定性还有一个,就是确定性卖出。”“懂得卖出才是师傅啊!他怎卖出呢?”“他介绍了五种离场的方法。”朱公扳起拇指,“首先是持股公司经营困难;如果企业产品的毛利率有下降趋势,最终得到确认,就会坚决卖掉股.票。”“林园还提醒投资者说,股市最
- 如果你想在淘宝上赚钱,这5种模式是绝对不能错过的!
氧惠_飞智666999
淘宝是国内最大的在线购物平台之一,也是最佳的创业平台之一。到目前为止,已经有无数的商家和个人成为淘宝的卖家,每天都有成千上万的交易在淘宝上完成。那么,淘宝上有哪些赚钱的方法呢?下面,我们将为您介绍一些淘宝上赚钱的模式。氧惠APP,2023全新模式,0投资,最快63天做到月入十万。我的直推也会放到你下面,我曾经1年做到百万团队,现在加入我也会帮你做到百万团队。【氧惠】百度有几百万篇报道,也期待你的加
- 暑期自学嵌入式——Day02(C语言阶段)
一位搞嵌入式的 genius
嵌入式自学专栏linux嵌入式C语言
点关注不迷路哟。你的点赞、收藏,一键三连,是我持续更新的动力哟!!!主页:一位搞嵌入式的genius-CSDN博客https://blog.csdn.net/m0_73589512?spm=1000.2115.3001.5343目录Day02→数据类型(上)数据类型分类基本数据类型整形数据类型字符型数据类型实型数据类型构造数据类型特殊数据类型布尔类型详解基本概念使用注意事项预处理分析知识小结Day
- 暑期自学嵌入式——Day03(C语言阶段)
一位搞嵌入式的 genius
嵌入式自学专栏c语言开发语言linux嵌入式C语言
个人主页:一位搞嵌入式的genius-CSDN博客https://blog.csdn.net/m0_73589512?spm=1010.2135.3001.5343点关注不迷路哟。你的点赞、收藏,一键三连,是我持续更新的动力哟!!!目录Day03:输入输出(上)Day03→嵌入式开发输入输出(上)知识纲要数据输出1)C语言IO特性2)字符输出函数(putchar)例题:putchar函数应用3)编
- 暑期自学嵌入式——Day04(C语言阶段)
一位搞嵌入式的 genius
嵌入式自学专栏嵌入式C语言linux
点关注不迷路哟。你的点赞、收藏,一键三连,是我持续更新的动力哟!!!目录C语言控制语句控制语句if(上)一、控制语句分类1.基本结构与学习要求2.分支语句3.循环语句4.学习方法建议二、分支语句:if-else详解1.if语句概述2.if语句的常见形式(1)简化形式(省略else)(2)阶梯形式(elseif多分支)3.应用案例:输入分数评级题目要求设计思路与代码实现关键解析4.if语句的嵌套形式
- 惬意的周六
枫郁樰
2019年2月23日,星期六,晴。(柔者处上之大学历练——连载第281篇)周六的早晨,和以前相比实在是要惬意许多。闹钟也是从七点响到了九点才起。起床收拾一番之后,便开始着手洗衣服的事情,原本想着羽绒服和那些平常穿着的衣服用洗衣机洗的,但是后来又想着羽绒服不能用洗衣机来洗,也就去接了盆热水先主要洗洗衣服上比较脏的地方,这便花了好一段时间。然后又去洗漱间去洗整件衣服,因为所用的盆比较小,洗起来也就格外
- 创意PPT模板:好水灵的排版,还是熟悉的味道
LJ的学习笔记
大家好,我是爱学习的瞄代表。今天给广大职场人带来一份创意PPT模板(好水灵的排版)。【总览图】:【PPT展示】:【PPT模板特点】:1、创意PPT模板,前所未有的快感;2、几乎所有素材均可编辑,有型更有料;3、扁平设计,时下正流行;4、好水灵的排版,还是熟悉的味道【获取方式】:微信公众号:LJ的读书笔记(ljdushubiji)回复关键词“0505”,即可获取。
- Enum用法
不懂事的小屁孩
enum
以前的时候知道enum,但是真心不怎么用,在实际开发中,经常会用到以下代码:
protected final static String XJ = "XJ";
protected final static String YHK = "YHK";
protected final static String PQ = "PQ";
- 【Spark九十七】RDD API之aggregateByKey
bit1129
spark
1. aggregateByKey的运行机制
/**
* Aggregate the values of each key, using given combine functions and a neutral "zero value".
* This function can return a different result type
- hive创建表是报错: Specified key was too long; max key length is 767 bytes
daizj
hive
今天在hive客户端创建表时报错,具体操作如下
hive> create table test2(id string);
FAILED: Execution Error, return code 1 from org.apache.hadoop.hive.ql.exec.DDLTask. MetaException(message:javax.jdo.JDODataSto
- Map 与 JavaBean之间的转换
周凡杨
java自省转换反射
最近项目里需要一个工具类,它的功能是传入一个Map后可以返回一个JavaBean对象。很喜欢写这样的Java服务,首先我想到的是要通过Java 的反射去实现匿名类的方法调用,这样才可以把Map里的值set 到JavaBean里。其实这里用Java的自省会更方便,下面两个方法就是一个通过反射,一个通过自省来实现本功能。
1:JavaBean类
1 &nb
- java连接ftp下载
g21121
java
有的时候需要用到java连接ftp服务器下载,上传一些操作,下面写了一个小例子。
/** ftp服务器地址 */
private String ftpHost;
/** ftp服务器用户名 */
private String ftpName;
/** ftp服务器密码 */
private String ftpPass;
/** ftp根目录 */
private String f
- web报表工具FineReport使用中遇到的常见报错及解决办法(二)
老A不折腾
finereportweb报表java报表总结
抛砖引玉,希望大家能把自己整理的问题及解决方法晾出来,Mark一下,利人利己。
出现问题先搜一下文档上有没有,再看看度娘有没有,再看看论坛有没有。有报错要看日志。下面简单罗列下常见的问题,大多文档上都有提到的。
1、没有返回数据集:
在存储过程中的操作语句之前加上set nocount on 或者在数据集exec调用存储过程的前面加上这句。当S
- linux 系统cpu 内存等信息查看
墙头上一根草
cpu内存liunx
1 查看CPU
1.1 查看CPU个数
# cat /proc/cpuinfo | grep "physical id" | uniq | wc -l
2
**uniq命令:删除重复行;wc –l命令:统计行数**
1.2 查看CPU核数
# cat /proc/cpuinfo | grep "cpu cores" | u
- Spring中的AOP
aijuans
springAOP
Spring中的AOP
Written by Tony Jiang @ 2012-1-18 (转)何为AOP
AOP,面向切面编程。
在不改动代码的前提下,灵活的在现有代码的执行顺序前后,添加进新规机能。
来一个简单的Sample:
目标类:
[java]
view plain
copy
print
?
package&nb
- placeholder(HTML 5) IE 兼容插件
alxw4616
JavaScriptjquery jQuery插件
placeholder 这个属性被越来越频繁的使用.
但为做HTML 5 特性IE没能实现这东西.
以下的jQuery插件就是用来在IE上实现该属性的.
/**
* [placeholder(HTML 5) IE 实现.IE9以下通过测试.]
* v 1.0 by oTwo 2014年7月31日 11:45:29
*/
$.fn.placeholder = function
- Object类,值域,泛型等总结(适合有基础的人看)
百合不是茶
泛型的继承和通配符变量的值域Object类转换
java的作用域在编程的时候经常会遇到,而我经常会搞不清楚这个
问题,所以在家的这几天回忆一下过去不知道的每个小知识点
变量的值域;
package 基础;
/**
* 作用域的范围
*
* @author Administrator
*
*/
public class zuoyongyu {
public static vo
- JDK1.5 Condition接口
bijian1013
javathreadConditionjava多线程
Condition 将 Object 监视器方法(wait、notify和 notifyAll)分解成截然不同的对象,以便通过将这些对象与任意 Lock 实现组合使用,为每个对象提供多个等待 set (wait-set)。其中,Lock 替代了 synchronized 方法和语句的使用,Condition 替代了 Object 监视器方法的使用。
条件(也称为条件队列或条件变量)为线程提供了一
- 开源中国OSC源创会记录
bijian1013
hadoopsparkMemSQL
一.Strata+Hadoop World(SHW)大会
是全世界最大的大数据大会之一。SHW大会为各种技术提供了深度交流的机会,还会看到最领先的大数据技术、最广泛的应用场景、最有趣的用例教学以及最全面的大数据行业和趋势探讨。
二.Hadoop
&nbs
- 【Java范型七】范型消除
bit1129
java
范型是Java1.5引入的语言特性,它是编译时的一个语法现象,也就是说,对于一个类,不管是范型类还是非范型类,编译得到的字节码是一样的,差别仅在于通过范型这种语法来进行编译时的类型检查,在运行时是没有范型或者类型参数这个说法的。
范型跟反射刚好相反,反射是一种运行时行为,所以编译时不能访问的变量或者方法(比如private),在运行时通过反射是可以访问的,也就是说,可见性也是一种编译时的行为,在
- 【Spark九十四】spark-sql工具的使用
bit1129
spark
spark-sql是Spark bin目录下的一个可执行脚本,它的目的是通过这个脚本执行Hive的命令,即原来通过
hive>输入的指令可以通过spark-sql>输入的指令来完成。
spark-sql可以使用内置的Hive metadata-store,也可以使用已经独立安装的Hive的metadata store
关于Hive build into Spark
- js做的各种倒计时
ronin47
js 倒计时
第一种:精确到秒的javascript倒计时代码
HTML代码:
<form name="form1">
<div align="center" align="middle"
- java-37.有n 个长为m+1 的字符串,如果某个字符串的最后m 个字符与某个字符串的前m 个字符匹配,则两个字符串可以联接
bylijinnan
java
public class MaxCatenate {
/*
* Q.37 有n 个长为m+1 的字符串,如果某个字符串的最后m 个字符与某个字符串的前m 个字符匹配,则两个字符串可以联接,
* 问这n 个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
*/
public static void main(String[] args){
- mongoDB安装
开窍的石头
mongodb安装 基本操作
mongoDB的安装
1:mongoDB下载 https://www.mongodb.org/downloads
2:下载mongoDB下载后解压
- [开源项目]引擎的关键意义
comsci
开源项目
一个系统,最核心的东西就是引擎。。。。。
而要设计和制造出引擎,最关键的是要坚持。。。。。。
现在最先进的引擎技术,也是从莱特兄弟那里出现的,但是中间一直没有断过研发的
- 软件度量的一些方法
cuiyadll
方法
软件度量的一些方法http://cuiyingfeng.blog.51cto.com/43841/6775/在前面我们已介绍了组成软件度量的几个方面。在这里我们将先给出关于这几个方面的一个纲要介绍。在后面我们还会作进一步具体的阐述。当我们不从高层次的概念级来看软件度量及其目标的时候,我们很容易把这些活动看成是不同而且毫不相干的。我们现在希望表明他们是怎样恰如其分地嵌入我们的框架的。也就是我们度量的
- XSD中的targetNameSpace解释
darrenzhu
xmlnamespacexsdtargetnamespace
参考链接:
http://blog.csdn.net/colin1014/article/details/357694
xsd文件中定义了一个targetNameSpace后,其内部定义的元素,属性,类型等都属于该targetNameSpace,其自身或外部xsd文件使用这些元素,属性等都必须从定义的targetNameSpace中找:
例如:以下xsd文件,就出现了该错误,即便是在一
- 什么是RAID0、RAID1、RAID0+1、RAID5,等磁盘阵列模式?
dcj3sjt126com
raid
RAID 1又称为Mirror或Mirroring,它的宗旨是最大限度的保证用户数据的可用性和可修复性。 RAID 1的操作方式是把用户写入硬盘的数据百分之百地自动复制到另外一个硬盘上。由于对存储的数据进行百分之百的备份,在所有RAID级别中,RAID 1提供最高的数据安全保障。同样,由于数据的百分之百备份,备份数据占了总存储空间的一半,因而,Mirror的磁盘空间利用率低,存储成本高。
Mir
- yii2 restful web服务快速入门
dcj3sjt126com
PHPyii2
快速入门
Yii 提供了一整套用来简化实现 RESTful 风格的 Web Service 服务的 API。 特别是,Yii 支持以下关于 RESTful 风格的 API:
支持 Active Record 类的通用API的快速原型
涉及的响应格式(在默认情况下支持 JSON 和 XML)
支持可选输出字段的定制对象序列化
适当的格式的数据采集和验证错误
- MongoDB查询(3)——内嵌文档查询(七)
eksliang
MongoDB查询内嵌文档MongoDB查询内嵌数组
MongoDB查询内嵌文档
转载请出自出处:http://eksliang.iteye.com/blog/2177301 一、概述
有两种方法可以查询内嵌文档:查询整个文档;针对键值对进行查询。这两种方式是不同的,下面我通过例子进行分别说明。
二、查询整个文档
例如:有如下文档
db.emp.insert({
&qu
- android4.4从系统图库无法加载图片的问题
gundumw100
android
典型的使用场景就是要设置一个头像,头像需要从系统图库或者拍照获得,在android4.4之前,我用的代码没问题,但是今天使用android4.4的时候突然发现不灵了。baidu了一圈,终于解决了。
下面是解决方案:
private String[] items = new String[] { "图库","拍照" };
/* 头像名称 */
- 网页特效大全 jQuery等
ini
JavaScriptjquerycsshtml5ini
HTML5和CSS3知识和特效
asp.net ajax jquery实例
分享一个下雪的特效
jQuery倾斜的动画导航菜单
选美大赛示例 你会选谁
jQuery实现HTML5时钟
功能强大的滚动播放插件JQ-Slide
万圣节快乐!!!
向上弹出菜单jQuery插件
htm5视差动画
jquery将列表倒转顺序
推荐一个jQuery分页插件
jquery animate
- swift objc_setAssociatedObject block(version1.2 xcode6.4)
啸笑天
version
import UIKit
class LSObjectWrapper: NSObject {
let value: ((barButton: UIButton?) -> Void)?
init(value: (barButton: UIButton?) -> Void) {
self.value = value
- Aegis 默认的 Xfire 绑定方式,将 XML 映射为 POJO
MagicMa_007
javaPOJOxmlAegisxfire
Aegis 是一个默认的 Xfire 绑定方式,它将 XML 映射为 POJO, 支持代码先行的开发.你开发服 务类与 POJO,它为你生成 XML schema/wsdl
XML 和 注解映射概览
默认情况下,你的 POJO 类被是基于他们的名字与命名空间被序列化。如果
- js get max value in (json) Array
qiaolevip
每天进步一点点学习永无止境max纵观千象
// Max value in Array
var arr = [1,2,3,5,3,2];Math.max.apply(null, arr); // 5
// Max value in Jaon Array
var arr = [{"x":"8/11/2009","y":0.026572007},{"x"
- XMLhttpRequest 请求 XML,JSON ,POJO 数据
Luob.
POJOjsonAjaxxmlXMLhttpREquest
在使用XMlhttpRequest对象发送请求和响应之前,必须首先使用javaScript对象创建一个XMLHttpRquest对象。
var xmlhttp;
function getXMLHttpRequest(){
if(window.ActiveXObject){
xmlhttp:new ActiveXObject("Microsoft.XMLHTTP
- jquery
wuai
jquery
以下防止文档在完全加载之前运行Jquery代码,否则会出现试图隐藏一个不存在的元素、获得未完全加载的图像的大小 等等
$(document).ready(function(){
jquery代码;
});
<script type="text/javascript" src="c:/scripts/jquery-1.4.2.min.js&quo