并查集算法题
简要介绍:
并查集:
一种数据结构,将一个集合分为不相交的子集,在添加新的子集,合并现有子集,判断元素所在集合时时间复杂度接近常数级。常用于求连通子图和最小生成树的Kruskal算法。
操作:
makeSet: 初始化,给每个元素分配一个特定的id,以及一个指向自己的指针,表示每个元素都在一个大小为1的集合当中。
find: 查找某个元素的根元素。当两个元素拥有同样的根元素时,说明他们在同一个集合当中。为了使得时间复杂度接近常数级,在查找的过程中,可以更新指针指向根元素(代码中使用递归方法),有人称其为路径压缩。
Union: 满足条件则合并两个子集。如果没有特殊要求,将一个集合的根指向另一个集合的根即可。也可根据秩或者集合的大小来指定。
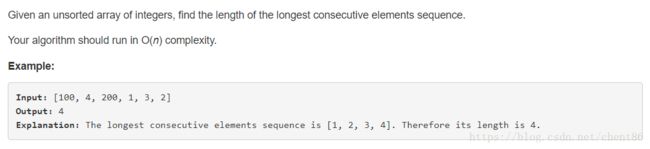
leetcode 128
思路: 使用并查集,比较两个数,如果他们的差为1,就进行合并。然后在将树a的根指向树b的根时(合并操作),将树a中的节点数添加到树b的节点数,最后从中找出最大的节点数即可。但这里忽略了一个问题,如果数组中的数存在重复,那么最终得到的数就会偏大。所以需要进行一下预处理。我们只需要给每个数一个唯一标识,然后判断出两个标识是否需要合并即可。
代码如下:
class Union_Set {
private:
int size;
int next[10000];
int child[10000];
public:
Union_Set(int size) {
this->size = size;
}
void makeSet() {
for(int i = 0; i < size; i++) {
next[i] = i;
child[i] = 1;
}
}
int find(int i) {
if(i != next[i])
next[i] = find(next[i]);
return next[i];
}
void Union(int i, int j) {
int a = find(i);
int b = find(j);
if(a != b) {
if(child[a] < child[b]) {
next[i] = b;
child[b] += child[a];
} else {
next[j] = a;
child[a] += child[b];
}
}
}
int max_child() {
int max = INT_MIN;
for(int i = 0; i < size; i++)
max = max& nums) {
map m;
int size = nums.size();
for(int i = 0; i < size; i++)
m.insert(pair(nums[i],i));
if(size == 0)
return 0;
Union_Set s(size);
s.makeSet();
for(auto&i:m) {
auto a = m.find(i.first-1);
auto b = m.find(i.first+1);
if(a != m.end())
s.Union(m[i.first-1],m[i.first]);
if(b != m.end())
s.Union(m[i.first+1],m[i.first]);
}
return s.max_child();
}
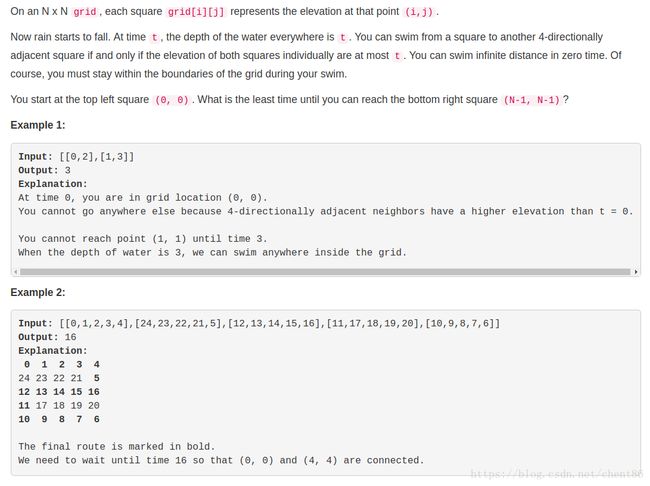
}; leetcode 778
思路:
首先想到是用BFS,对于给定的t执行BFS,如果能访问到终点,说明t满足条件。为了减少BFS的次数,可以采用二分的办法,选取指定的t。代码如下:
class Solution {
public:
int swimInWater(vector>& grid) {
int top = INT_MIN;
if(grid.size() == 0)
return 0;
int height = grid.size();
int width = grid[0].size();
for(int i = 0; i < height; i++)
for(int j = 0; j < width; j++) {
top = max(top, grid[i][j]);
}
pair end = make_pair(height-1,width-1);
int low = grid[0][0];
int x_diff[4] = {0,0,1,-1};
int y_diff[4] = {1,-1,0,0};
while(1) {
set> visited = {make_pair(0,0)};
queue> q;
q.push(make_pair(0,0));
int mid = (low+top)/2;
int s = q.size();
while(!q.empty()){
pair tmp = q.front();
q.pop();
for(int i = 0; i < 4; i++) {
if(tmp.first+x_diff[i] < 0 || tmp.first+x_diff[i] >= height ||
tmp.second+y_diff[i] <0 || tmp.second+y_diff[i] >= width)
continue;
if(grid[tmp.first+x_diff[i]][tmp.second+y_diff[i]] <= mid) {
pair n = pair(tmp.first+x_diff[i], tmp.second+y_diff[i]);
if(visited.find(n) == visited.end()) {
visited.insert(n);
q.push(n);
}
}
}
}
if(visited.find(end) != visited.end()) {
top = mid;
if(top == low)
return top;
} else {
if(mid == low)
return top;
low = mid;
}
}
}
}; 需要注意的是,二维矩阵的坐标原点位于左上角,(x,y)中的x实际是y轴的距离,y实际是x轴的距离(又有点生疏了),然后二分到最后的时候有两种情况,如果最后的mid不满足条件,那么low和top将一直保持为low=mid, top=mid+1,此时应该选择top为答案。而如果最后的mid满足条件,top和low将合并,也选择top为答案即可。
但这个算法复杂度有点高,只beat 10%+。那么再来考虑下使用并查集。
并查集的结构不变,在合并时选择将rank低的根指向rank高的根可以降低树高,提高查找效率。代码如下:
class Union_Set {
private:
int size;
vector next;
vector rank;
public:
Union_Set(int size) {
this->size = size;
next.resize(size);
rank.resize(size);
}
void makeSet() {
for(int i = 0; i < size; i++) {
next[i] = i;
rank[i] = 1;
}
}
int find(int i) {
if(i != next[i])
next[i] = find(next[i]);
return next[i];
}
void Union(int i, int j) {
int root_i = find(i);
int root_j = find(j);
if(root_i != root_j) {
if(rank[root_i] < rank[root_j]) {
next[root_i] = root_j;
rank[root_j] += rank[root_i];
}
else {
next[root_j] = root_i;
rank[root_i] += rank[root_j];
}
}
}
}; 那么如何使用并查集呢?我们将之前的算法中的BFS改为并查集算法即可,当二分法选取出一个t值时,我们遍历一遍所有坐标,如果这个坐标的值不大于t,那么将它与它上下左右的值不大于t的坐标纳入同一个集合中。处理完之后如果起点和终点在一个集合中,说明这个t值满足条件。(需要注意每次处理之前都要重新调用makeSet,清理上次处理的结果)
class Solution {
public:
int swimInWater(vector>& grid) {
if(grid.size() == 0)
return 0;
int height = grid.size();
int width = grid[0].size();
int top = width*height-1;
Union_Set s(height*width);
int low = grid[0][0];
int x_diff[4] = {0,0,1,-1};
int y_diff[4] = {1,-1,0,0};
while(1) {
s.makeSet();
int mid = (low+top)/2;
for(int j = 0; j < height; j++)
for(int k = 0; k < width; k++) {
if(grid[j][k] > mid)
continue;
for(int i = 0; i < 4; i++) {
if(j+x_diff[i] < 0 || j+x_diff[i] >= height ||
k+y_diff[i] <0 || k+y_diff[i] >= width)
continue;
if(grid[j+x_diff[i]][k+y_diff[i]] <= mid) {
s.Union(j*width+k,(j+x_diff[i])*width+(k+y_diff[i]));
}
}
}
if(s.find(0) == s.find(width*height-1)) {
top = mid;
if(top == low)
return top;
} else {
if(mid == low)
return top;
low = mid;
}
}
}
}; 然后效率得到了提升,beat 30%+。那么同样使用并查集,还有更快的算法吗?参考下他人的算法,这样写可以beat 98%,代码如下:
class Solution {
public:
int swimInWater(vector>& grid) {
if(grid.size() == 0)
return 0;
int size = grid.size();
Union_Set s(size*size);
s.makeSet();
vector> v;
v.resize(size*size);
for(int i = 0; i < size; i++)
for(int j = 0; j < size; j++) {
v[grid[i][j]] = make_pair(i,j);
}
int x_diff[4] = {0,0,1,-1};
int y_diff[4] = {1,-1,0,0};
for(int t = 0; t < size*size; t++) {
pair tmp = v[t];
for(int i = 0; i < 4; i++) {
if(tmp.first+x_diff[i] < 0 || tmp.first+x_diff[i] >= size ||
tmp.second+y_diff[i] <0 || tmp.second+y_diff[i] >= size)
continue;
if(grid[tmp.first+x_diff[i]][tmp.second+y_diff[i]] <= t) {
s.Union(tmp.first*size+tmp.second,(tmp.first+x_diff[i])*size+(tmp.second+y_diff[i]));
}
}
if(s.find(0) == s.find(size*size-1)) {
return t;
}
}
}
}; 思路就是,因为二维矩阵是一个n x n的矩阵,且为0到(n x n) - 1 的置换。t从0开始逐1增加,每增一次就对那个刚好满足的坐标进行一次同样的处理(上下左右是否满足不大于t,满足则Union)。在这一次遍历的过程中,如果起点和终点在同一个集合中,那么此时t就是满足条件的最小t。
至于这个算法的正确性证明,我也不太清楚,欢迎评论解答。
实际上不使用并查集也可以达到相同的运行时间。使用类似于Prim算法求最小生成树的算法,S = {}, 初始时将原点添加到S中,然后每次从S中删除值最小的点,记录它的值到集合P,再将它邻接的没有访问过的点加入S中。当删除的点为终点时,集合P中最大的值即为最小的t值。代码如下,使用优先队列以减少复杂度(此代码来自评论,侵删):
struct Pos {
int x;
int y;
int elevation;
Pos(int xx, int yy, int e) {
x = xx;
y = yy;
elevation = e;
}
};
struct PosComparer {
bool operator()(const Pos &left, const Pos&right) {
return left.elevation > right.elevation;
}
};
class Solution {
public:
int swimInWater(vector>& grid) {
int m = grid.size();
if (m <= 0) {
return 0;
}
int n = grid[0].size();
if (n <= 0) {
return 0;
}
if (m == 1 && n == 1) {
return 0;
}
vector> directions{ { 0,1 },{ 0,-1 },{ 1,0 },{ -1,0 } };
priority_queue, PosComparer> q;
vector> inQueue(m, vector(n));
q.push(Pos(0, 0, grid[0][0]));
inQueue[0][0] = true;
int result = 0;
while (q.size() > 0) {
auto curPos = q.top();
q.pop();
result = max(result, curPos.elevation);
if (curPos.x == m - 1 && curPos.y == n - 1) {
return result;
}
for (int i = 0; i < directions.size(); i++) {
int nx = curPos.x + directions[i][0];
int ny = curPos.y + directions[i][1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !inQueue[nx][ny]) {
inQueue[nx][ny] = true;
q.push(Pos(nx, ny, grid[nx][ny]));
}
}
}
return INT_MAX;
}
};