【机器学习】算法实现感知机与神经元分类器(概念+图+实战)
本文代码推荐使用Jupyter notebook跑,这样得到的结果更为直观。
感知机
MCP神经元和罗森布拉特筏值感知机的理念:
通过模拟的方式还原大脑中单个神经元的工作方式(是否被激活)
罗森布拉特筏值感知机最初的规则:
将权重初始化为0或者一个极小的数
迭代所有训练样本x
计算输出值y
更新权重
把分类问题看作一个二值分类任务,一般记为1和-1。
定义一个激励函数,激励函数以特定的输入值x与相应的权值向量w的线性组合作为输入。如果激励函数的输出值大于预设的筏值θ,将其分到1类,否则分到-1类。
感知机算法中,激励函数是一个简单的分段函数。
权重w的更新方式为:wj = wj +用于更新wj的值
更新权重wj的值 = n(yi - ^yi)xj
n为学习速率,介于0-1之间的常数
^yi为预测得到的类标
权重值是同时更新的
感知机收敛的前提:两个类别必须是线性可分的,且学习速率足够小
感知机不收敛会不断的更新权值,解决办法:
设置迭代次数最大值,强制停止感知机
设置允许错误分类样本的筏值
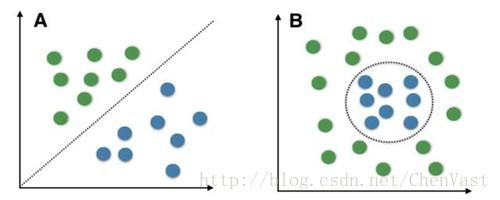
线性可分与非线性可分:
python实现感知机算法:
import numpy as np
class Perceptron(object):
"""感知器分类器
参数
------------
eta : float
学习速率 (between 0.0 and 1.0)
n_iter : int
通过训练数据集
属性
-----------
w_ : 1d-array
加权拟合后.
errors_ : list
每一个时代的错误分类数目。
"""
def __init__(self, eta=0.01, n_iter=10):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
"""训练数据。
参数
----------
X : {array-like}, shape = [n_samples, n_features]
培训向量,n_samples样品和n_features的数量特征的数量。
y : array-like, shape = [n_samples]
目标的值。
Returns
-------
self : object
"""
self.w_ = np.zeros(1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
"""计算净输入"""
# 计算向量点积
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
"""在单位步骤后返回类标签。计算和预测类标"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
Numpy用于算术运算向量化,C语言实现的python科学计算库。
向量化的好处:一个算术运算操作会自动应用到数组中的所有元素上
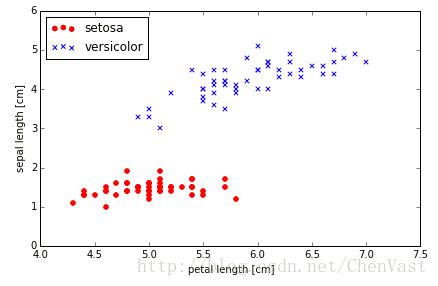
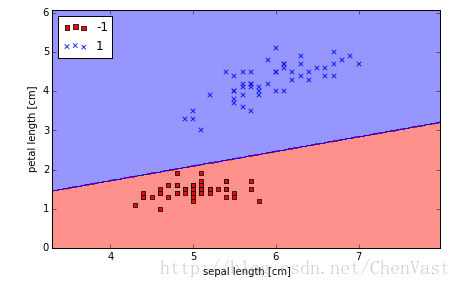
基于鸢尾花数据集训练了感知机模型:
# 1、获取数据集
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/iris/iris.data', header=None)
print(df.tail())
#/2、抽取100个类标,50个setosa和50个versicolor,显示二维散点图。
import matplotlib.pyplot as plt
import numpy as np
#选择setosa和杂色的
y = df.iloc[0:100, 4].values
# 1代表versicolor,-1代表setosa
y = np.where(y == 'Iris-setosa', -1, 1)
# 提取萼片长度和花瓣长度。
X = df.iloc[0:100, [0, 2]].values
# plot data
plt.scatter(X[:50, 0], X[:50, 1],
color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1],
color='blue', marker='x', label='versicolor')
plt.xlabel('petal length [cm]')
plt.ylabel('sepal length [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./iris_1.png', dpi=300)
plt.show()
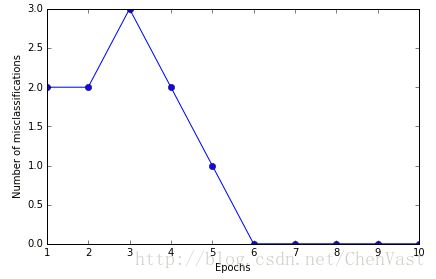
# 3、取数据集训练感知机模型,显示错误分类数量和迭代次数的折线图
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of misclassifications')
plt.tight_layout()
# plt.savefig('./perceptron_1.png', dpi=300)
plt.show()
# 4、显示二维数据集决策边界
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./perceptron_2.png', dpi=300)
plt.show()
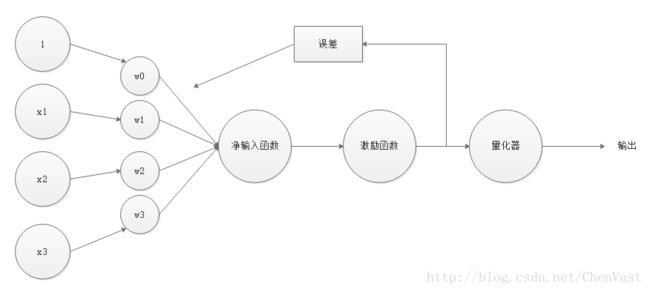
自适应线性神经元:
单层神经网络:自适应线性神经元
Adaline算法:阐明代价函数的核心概念,对其做了最小化优化。
Adaline权重更新:通过一个连续的线性激励函数完成
Adaline的激励函数是简单的恒等函数
线性激励函数在权重更新时,使用量化器对类标进行预测,量化器与单位跃阶函数类似。
使用线性激励函数的连续型输出值,而不是而类别分类类标来计算模型的误差以及更新权重。
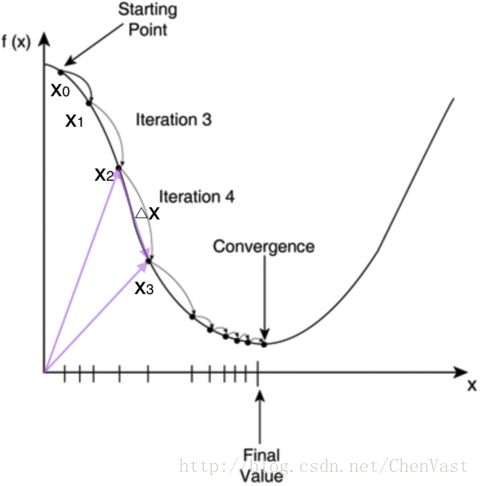
使用梯度下降最小化代价函数
监督学习算法的一个核心组成:在学习阶段定义一个待优化的目标函数。
这个目标函数通常是需要做最小化处理的代价函数。
可以将代价函数定义为通过模型得到输出与实际类标之间的误差平方和。
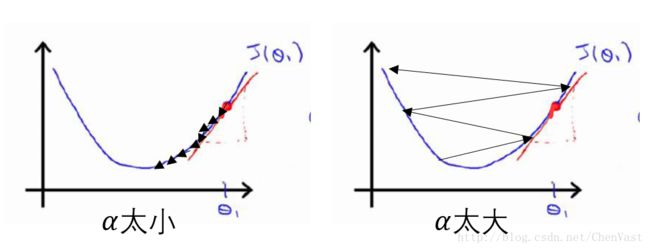
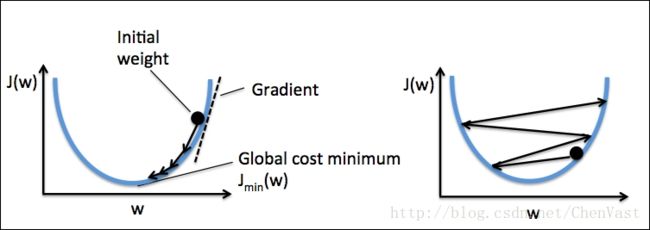
连续型激励函数主要优点是可导,而且是一个凸函数,这样可以通过简单高效的梯度下降算法来得到权重。
梯度下降图:
为了计算代价函数的梯度,计算代价函数相对于每个权重的偏导。
学习速率和代价函数称为Adaline算法的超参。
python实现自适应线性神经元:
class AdalineGD(object):
"""ADAptive LInear NEuron classifier.
Parameters
------------
eta : float
Learning rate (between 0.0 and 1.0)
n_iter : int
Passes over the training dataset.
Attributes
-----------
w_ : 1d-array
Weights after fitting.
errors_ : list
Number of misclassifications in every epoch.
"""
def __init__(self, eta=0.01, n_iter=50):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
""" Fit training data.
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
"""
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""Compute linear activation"""
return self.net_input(X)
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.activation(X) >= 0.0, 1, -1)
# 标准化的特征
X_std = np.copy(X)
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()
ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)
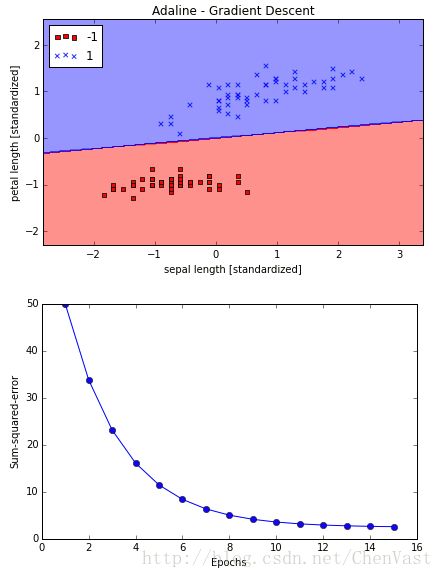
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./adaline_2.png', dpi=300)
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')
plt.tight_layout()
# plt.savefig('./adaline_3.png', dpi=300)
plt.show()
# 绘制两种不同学习速率下,代价函数与迭代次数的图像。
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))
ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.tight_layout()
# plt.savefig('./adaline_1.png', dpi=300)
plt.show()
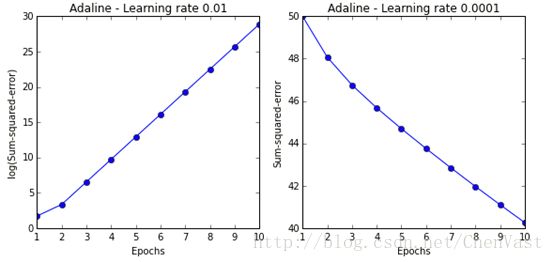
第一张图的学习速率过大跳过全局最优解,导致误差随迭代次数上升而上升。
学习率过大的效果图:
随机梯度下降:
大数据集使用梯度下降成本高昂,随机梯度下降能解决这个问题。
随机梯度下降也称为迭代梯度下降或者在线梯度下降。
随机梯度下降更容易跳出最小范围的局部最优解,为了得到更加准确的结果,让数据随机提供给算法是非常重要的,防止每次迭代打乱训练集以防进入死循环。
随机梯度下降的学习速率随着时间变化的:n = c1/(迭代次数+c2),c1 c2为常数。
随机梯度下降可将用于在线学习,有新的数据输入时模型会被实时训练。
随机梯度下降:
大数据集使用梯度下降成本高昂,随机梯度下降能解决这个问题。
随机梯度下降也称为迭代梯度下降或者在线梯度下降。
随机梯度下降更容易跳出最小范围的局部最优解,为了得到更加准确的结果,让数据随机提供给算法是非常重要的,防止每次迭代打乱训练集以防进入死循环。
随机梯度下降的学习速率随着时间变化的:n = c1/(迭代次数+c2),c1 c2为常数。
随机梯度下降可将用于在线学习,有新的数据输入时模型会被实时训练。
python实现随机梯度下降:
from numpy.random import seed
class AdalineSGD(object):
"""ADAptive LInear NEuron classifier.
Parameters
------------
eta : float
Learning rate (between 0.0 and 1.0)
n_iter : int
Passes over the training dataset.
Attributes
-----------
w_ : 1d-array
Weights after fitting.
errors_ : list
每一个迭代的错误分类数目。
shuffle : bool (default: True)
如果要防止循环的话,每个阶段都要训练数据。
random_state : int (default: None)
设置随机状态,以调整和初始化权重。
"""
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False
self.shuffle = shuffle
if random_state:
seed(random_state)
def fit(self, X, y):
""" 训练数据。
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
"""
self._initialize_weights(X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
if self.shuffle:
X, y = self._shuffle(X, y)
cost = []
for xi, target in zip(X, y):
cost.append(self._update_weights(xi, target))
avg_cost = sum(cost)/len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self, X, y):
"""在不重新初始化权重的情况下调整训练数据。"""
if not self.w_initialized:
self._initialize_weights(X.shape[1])
if y.ravel().shape[0] > 1:
for xi, target in zip(X, y):
self._update_weights(xi, target)
else:
self._update_weights(X, y)
return self
def _shuffle(self, X, y):
""打乱训练数据"""
r = np.random.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self, m):
"""初始化权重为零"""
self.w_ = np.zeros(1 + m)
self.w_initialized = True
def _update_weights(self, xi, target):
"""应用Adaline学习规则更新权重"""
output = self.net_input(xi)
error = (target - output)
self.w_[1:] += self.eta * xi.dot(error)
self.w_[0] += self.eta * error
cost = 0.5 * error**2
return cost
def net_input(self, X):
"""计算净输入"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""计算线性激活"""
return self.net_input(X)
def predict(self, X):
"""在单位步骤后返回类标签。"""
return np.where(self.activation(X) >= 0.0, 1, -1)
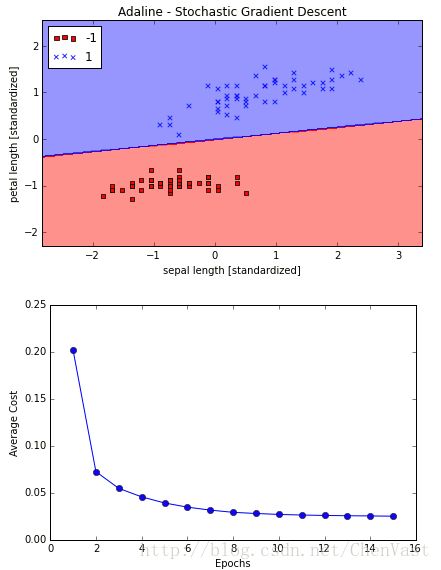
ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Stochastic Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
#plt.savefig('./adaline_4.png', dpi=300)
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Average Cost')
plt.tight_layout()
# plt.savefig('./adaline_5.png', dpi=300)
plt.show()