博弈论经典算法(一)——对抗搜索与Alpha-Beta剪枝
前言
在一些复杂的博弈论题目中,每一轮操作都可能有许多决策,于是就会形成一棵庞大的博弈树。
而有一些博弈论题没有什么规律,针对这样的问题,我们就需要用一些十分玄学的算法。
例如对抗搜索。
对抗搜索简介
一、 对抗搜索的适用范围
在博弈论题目中,如果决策双方的获胜条件是截然相反的,即一方要求得分越高越好,另一方要求得分越低越好,这时我们就可以用上对抗搜索算法。
二、对抗搜索的主要思想
对抗搜索的核心思想就是 d f s dfs dfs遍历一遍博弈树。
不难想到,如果博弈树非常庞大,在不加优化的情况下,对抗搜索的时间效率是十分低下的。
因此,我们就需要对对抗搜索进行一定的优化。
三、对抗搜索的优化
对抗搜索的优化一般来讲有两种:记忆化和 A l p h a − B e t a Alpha-Beta Alpha−Beta剪枝 。
不过需要注意,如果两个优化一起使用,很可能会产生化学反应出现一些奇妙的 B u g Bug Bug(我已经亲身体验过了)。
对抗搜索优化一:记忆化
记忆化应该是搜索中一个比较常用的技巧。
一、大致思路
它的大致思路就是,对于当前的某一种状态,在求解后将结果记录下来,下一次再访问到时直接将存下来的结果返回即可。
二、模板
记忆化优化对抗搜索的伪代码如下:
inline int dfs(Status s,int Which)//Status记录当前状态,Which记录当前操作的选手,其中0号选手取Max,1号选手取Min
{
if(res[s]) return res[s];//如果之前已经求出过这个状态的结果,直接返回
if(IsEnd(s)) return GetVal(s);//如果当前状态已经为最终状态,就返回当前状态的分值
register int i,ans=Which?1e9:0;
expend(s);//扩展当前状态,并将新状态存储于NewStatus数组中,用NewStatusTotal记录新状态的数量
for(i=1;i<=NewStatusTotal;++i)//枚举从当前状态能够扩展到的新状态
ans=Which?min(ans,dfs(NewStatus[i],Which^1):max(ans,dfs(NewStatus[i],Which^1);//不断dfs,更新ans
return res[s]=ans;//将最终求解出的结果存储下来
}
对抗搜索优化二: A l p h a − B e t a Alpha-Beta Alpha−Beta剪枝
A l p h a − B e t a Alpha-Beta Alpha−Beta剪枝应该是对抗搜索一个比较巧妙的优化。
一、大致思路
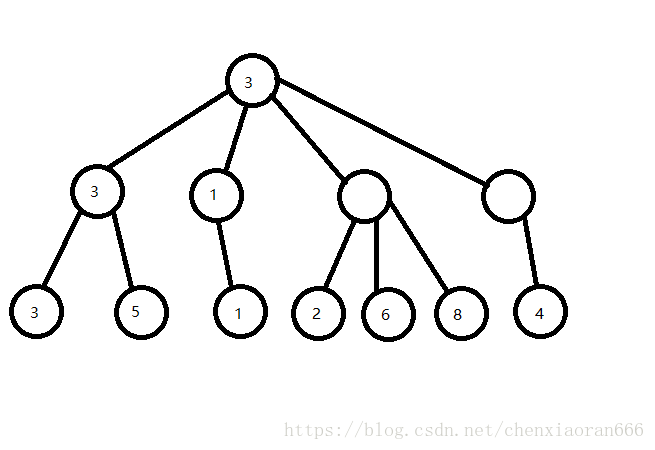
如图是一棵博弈树:
假设第一个决策者的目的是取最大值,第二个决策者的目的是取最小值。
在搜索完根节点的两个子节点后,博弈树就会变成这样:
不难发现,在处理完第三个节点的第一个子节点之后,第三个节点的权值就会变成 2 2 2。
因为第三个节点的目标是取最小值,因此最终第三个节点的权值必定小于等于 2 2 2。
而根节点的目标是取最大值,且此时根节点的权值已经为 3 3 3了。
也就是说,第三个节点对最终答案肯定是没有任何贡献的。
因此对于第三个节点的剩余两个状态,我们就无需继续搜索了,可以直接退出。
这就是传说中的 A l p h a − B e t a Alpha-Beta Alpha−Beta剪枝了。
二、模板
A l p h a − B e t a Alpha-Beta Alpha−Beta剪枝优化对抗搜索的伪代码如下:
inline int dfs(Status s,int Alpha,int Beta,int Which)//Status记录当前状态,Which记录当前操作的选手,其中0号选手取Max,1号选手取Min
//Alpha存储较大值,Beta存储较小值
//如果当前节点是取Max的节点,则Alpha表示当前节点父亲的父亲的权值,Beta表示当前节点父亲的权值
//如果当前节点是取Min的节点,则Alpha表示当前节点父亲的权值,Beta表示当前节点父亲的父亲的权值
{
if(IsEnd(s)) return GetVal(s);//如果当前状态已经为最终状态,就返回当前状态的分值
register int i;
expend(s);//扩展当前状态,并将新状态存储于NewStatus数组中,用NewStatusTotal记录新状态的数量
for(i=1;i<=NewStatusTotal;++i)//枚举从当前状态能够扩展到的新状态
{
t=dfs(NewStatus,Alpha,Beta,Which^1);//求出当前枚举到的新状态的分值
(s.Which?Beta=min(Beta,t):Alpha=max(Alpha,t)); //如果当前节点取min,就更新Beta,否则更新Alpha
if(Alpha>=Beta) break;//如果Alpha≥Beta,就说明这个节点对最终答案没有贡献了,就结束搜索
}
return s.Which?Beta:Alpha;//返回相应值
}
后记
对抗搜索的核心内容差不多也就是这些。
但是,如果真正用起来,对抗搜索其实还是挺复杂的。
下面推荐一道例题:【BZOJ3106】[CQOI2013] 棋盘游戏
L i n k Link Link
【BZOJ3106】[CQOI2013] 棋盘游戏 的题解 详见博客【BZOJ3106】[CQOI2013] 棋盘游戏(对抗搜索)