【LeetCode】—— 二叉树的深度

一、LeetCode104题 二叉树的最大深度

1.1 题目描述

定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

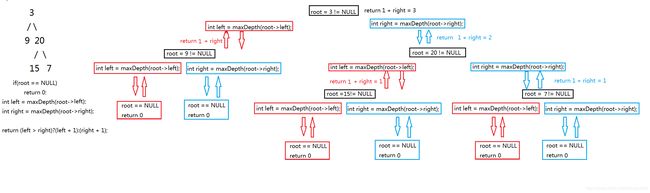
给定二叉树 [3,9,20,null,null,15,7]，

    3    
   / \   
  9  20
    /  \    
   15   7 
返回它的最大深度 3 。

1.2 解题思路

递归求解

1.3 代码实现

递归求解

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        
        return (left > right)?(left + 1):(right + 1);
    }
};

非递归(迭代)求解

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        int num = 0;
        queue  que;
        que.push(root);
        while(!que.empty()){
            int n = que.size();
            for(int i = 0;i < n;++i){
                TreeNode *cur = que.front();
                if(cur->left != NULL)
                    que.push(cur->left);
                if(cur->right != NULL)
                    que.push(cur->right);
                que.pop();
            }
            num++;
        }
        return num;
    }
};

二、LeetCode11题 二叉树的最小深度

2.1 题目描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

      3   
     / \ 
    9  20
      /  \    
     15   7 

返回它的最小深度 2.

2.2 解题思路

• 思路和求二叉树的最大深度相似，只是返回的是左右子树小的一个。
• 需要注意的点是，若左子树或是右子树不存在时，此时计算的是存在子树的高度，而不是只计算根节点的高度
• 举个例子：

            1
             \
              2

• 此时树的最小高度不是1，而是2，因为左子树不存在，所以此时计算的是右子树的高度。

2.3 代码实现

class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        if(!root->left && !root->right)
            return 1;
        
        int left = minDepth(root->left);
        int right = minDepth(root->right);
        
        if(!left)
            return 1 + right;
        if(!right)
            return 1 + left;
        
        return min(left,right) + 1; 
        
    }
};

三、LeetCode110题 平衡二叉树

3.1 题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

      3  
     / \   
    9  20
      /  \    
     15   7 

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \   
   3   3 
  / \  
 4   4 

返回 false 。

3.2 解题思路

• C++实现，思路很简单，主要控制好递归即可，这里借助了求二叉树高度的函数， 求出左右子树的高度，差值若是大于一则不是平衡二叉树，之后递归检查二叉树的左右子树， 若左子树不平衡则不用检查右子树，直接返回false给上层递归，反之继续检查右子树 若左右子树均平衡，则返回true给上层递归

3.3 代码实现

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        
        return (left > right)?(left + 1):(right + 1);
    }
    bool isBalanced(TreeNode* root) {
        if(root == NULL)
            return true;
        if(abs(maxDepth(root->left) - maxDepth(root->right)) > 1)
            return false;
        else
        {
            if(isBalanced(root->left) == false)
                 return false;
            if(isBalanced(root->right) == false)
                 return false;
            return true;
        }   
    }
};