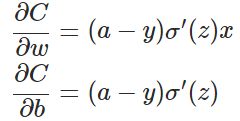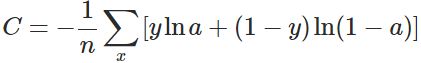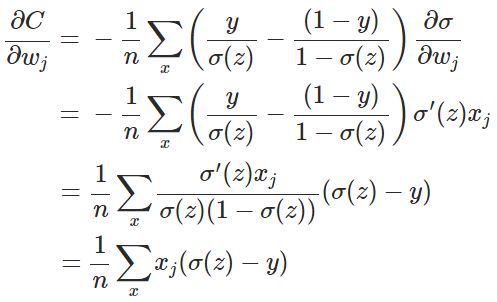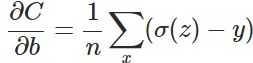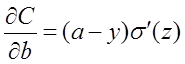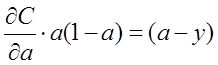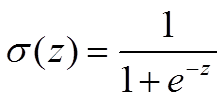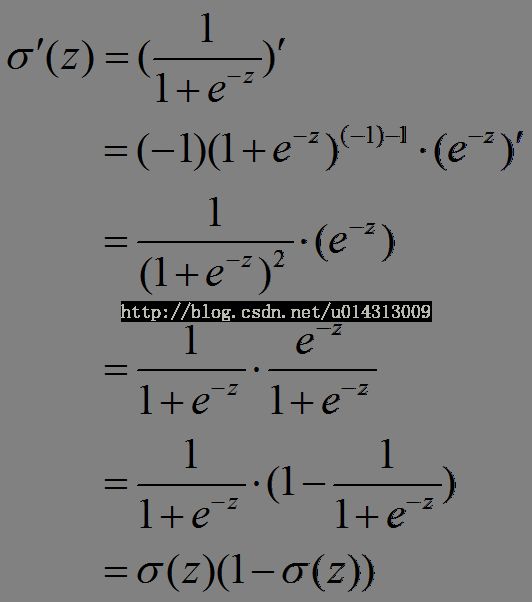交叉熵代价函数（作用及公式推导）
转自：http://m.blog.csdn.net/u014313009/article/details/51043064
http://blog.sina.com.cn/s/blog_80ce3a550102wko1.html
交叉熵代价函数（Cross-entropy cost function）是用来衡量人工神经网络（ANN）的预测值与实际值的一种方式。与二次代价函数相比，它能更有效地促进ANN的训练。在介绍交叉熵代价函数之前，本文先简要介绍二次代价函数，以及其存在的不足。
1. 二次代价函数的不足
ANN的设计目的之一是为了使机器可以像人一样学习知识。人在学习分析新事物时，当发现自己犯的错误越大时，改正的力度就越大。比如投篮：当运动员发现自己的投篮方向离正确方向越远，那么他调整的投篮角度就应该越大，篮球就更容易投进篮筐。同理，我们希望：ANN在训练时，如果预测值与实际值的误差越大，那么在反向传播训练的过程中，各种参数调整的幅度就要更大，从而使训练更快收敛。然而，如果使用二次代价函数训练ANN，看到的实际效果是，如果误差越大，参数调整的幅度可能更小，训练更缓慢。
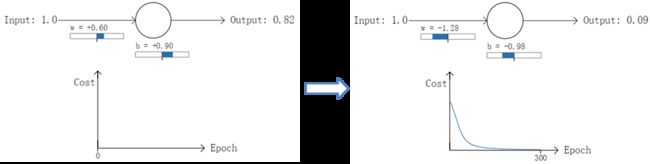
以一个神经元的二类分类训练为例，进行两次实验（ANN常用的激活函数为sigmoid函数，该实验也采用该函数）：输入一个相同的样本数据x=1.0（该样本对应的实际分类y=0）；两次实验各自随机初始化参数，从而在各自的第一次前向传播后得到不同的输出值，形成不同的代价（误差）：
实验1：第一次输出值为0.82
实验2：第一次输出值为0.98
在实验1中，随机初始化参数，使得第一次输出值为0.82（该样本对应的实际值为0）；经过300次迭代训练后，输出值由0.82降到0.09，逼近实际值。而在实验2中，第一次输出值为0.98，同样经过300迭代训练，输出值只降到了0.20。
从两次实验的代价曲线中可以看出：实验1的代价随着训练次数增加而快速降低，但实验2的代价在一开始下降得非常缓慢；直观上看，初始的误差越大，收敛得越缓慢。
其实，误差大导致训练缓慢的原因在于使用了二次代价函数。二次代价函数的公式如下：
其中，C表示代价，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。为简单起见，同样一个样本为例进行说明，此时二次代价函数为：
目前训练ANN最有效的算法是反向传播算法。简而言之，训练ANN就是通过反向传播代价，以减少代价为导向，调整参数。参数主要有：神经元之间的连接权重w，以及每个神经元本身的偏置b。调参的方式是采用梯度下降算法（Gradient descent），沿着梯度方向调整参数大小。w和b的梯度推导如下：
其中，z表示神经元的输入，
表示激活函数。从以上公式可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。而神经网络常用的激活函数为sigmoid函数，该函数的曲线如下所示：
如图所示，实验2的初始输出值（0.98）对应的梯度明显小于实验1的输出值（0.82），因此实验2的参数梯度下降得比实验1慢。这就是初始的代价（误差）越大，导致训练越慢的原因。与我们的期望不符，即：不能像人一样，错误越大，改正的幅度越大，从而学习得越快。
可能有人会说，那就选择一个梯度不变化或变化不明显的激活函数不就解决问题了吗？图样图森破，那样虽然简单粗暴地解决了这个问题，但可能会引起其他更多更麻烦的问题。而且，类似sigmoid这样的函数（比如tanh函数）有很多优点，非常适合用来做激活函数，具体请自行google之。
2. 交叉熵代价函数
换个思路，我们不换激活函数，而是换掉二次代价函数，改用交叉熵代价函数：
其中，x表示样本，n表示样本的总数。那么，重新计算参数w的梯度：
其中（具体证明见附录）：
因此，w的梯度公式中原来的
被消掉了；另外，该梯度公式中的
表示输出值与实际值之间的误差。所以，当误差越大，梯度就越大，参数w调整得越快，训练速度也就越快。同理可得，b的梯度为：
实际情况证明，交叉熵代价函数带来的训练效果往往比二次代价函数要好。
3. 交叉熵代价函数是如何产生的？
以偏置b的梯度计算为例，推导出交叉熵代价函数：
在第1小节中，由二次代价函数推导出来的b的梯度公式为：
为了消掉该公式中的，我们想找到一个代价函数使得：
即：
对两侧求积分，可得：
而这就是前面介绍的交叉熵代价函数。
附录：
sigmoid函数为：
可证：
KL 散度
相对熵（KL散度）
如何通俗的解释交叉熵与相对熵?
熵、KL散度、信息增益、互信息-学习笔记
JS散度是利用KL散度来得到的。JS是对称的而且值是有界的[0,1].
P,Q和第三个分布进行KL计算（第三个分布：（P+Q）/2 ）
4. Earth Mover's Distance —— 推土机距离 又称为 Wasserstein距离
