四种 图的最短路径算法

原文：

https://www.cnblogs.com/chuninggao/p/7301082.html

图的最短路径：Dijkstra、Bellman-Ford、SPFA、Floyd、A*算法

图的表示方法

最常用的表示图的方法是邻接矩阵与邻接表。

邻接矩阵表示法

设G是一个有n(n>0)个顶点的图，V(G)={v1, v2, …, vn}，则邻接矩阵AG是一个n阶二维矩阵。在该矩阵中，如果vi至vj有一条边，则(i, j)项的值为1，否则为0，即：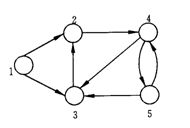 

 
邻接矩阵的实现很简单：

int edge[n][n]={0};

for(...){
    ...
    //无向图的邻接矩阵表示
    edge[node1][node2]=1;
    edge[node2][node1]=1;
}

邻接表表示法

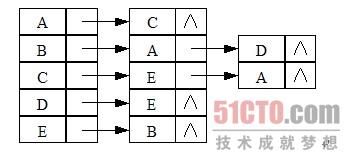
设G是一个有n(n>0)个顶点的图，V(G)={v1, v2, …, vn}。在邻接表中，每个顶点v都对应着一个链表，该链表的每个节点都包含一个顶点u，且(v, u)∈E(G)。因为图中有n个顶点，所以可以利用一个长度为n的数组A，A(i)指向第i个顶点对应的链表的第一个节点，链表由顶点vi的全部邻接顶点组成。

 
实现邻接表时，可以不用链表，而是用vector数组的形式。

vector adj[MAX];
for(int i=1;i<=n-1;i++) {
    cin>>a>>b;
    //构建无向图的邻接表
    adj[a].push_back(b);
    adj[b].push_back(a);
        }

•  

其中，adj[i]是一个vector，它记录了结点i连通的所有结点。

Dijkstra算法

1.定义概览

Dijkstra（迪杰斯特拉）算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

2.算法描述

求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。 
 
这里使用二维数组e来存储顶点之间边的关系，初始值如下： 
 
我们还需要用一个一维数组dis来存储1号顶点到其余各个顶点的初始路程，如下。 
 
我们将此时dis数组中的值称为最短路的“估计值”。

既然是求1号顶点到其余各个顶点的最短路程，那就先找一个离1号顶点最近的顶点。通过数组dis可知当前离1号顶点最近是2号顶点。当选择了2号顶点后，dis[2]的值就已经从“估计值”变为了“确定值”，即1号顶点到2号顶点的最短路程就是当前dis[2]值。

既然选了2号顶点，接下来再来看2号顶点有哪些出边呢。有2->3和2->4这两条边。先讨论通过2->3这条边能否让1号顶点到3号顶点的路程变短。也就是说现在来比较dis[3]和dis[2]+e[2][3]的大小。其中dis[3]表示1号顶点到3号顶点的路程。dis[2]+e[2][3]中dis[2]表示1号顶点到2号顶点的路程，e[2][3]表示2->3这条边。所以dis[2]+e[2][3]就表示从1号顶点先到2号顶点，再通过2->3这条边，到达3号顶点的路程。

我们发现dis[3]=12，dis[2]+e[2][3]=1+9=10，dis[3]>dis[2]+e[2][3]，因此dis[3]要更新为10。这个过程有个专业术语叫做“松弛”。即1号顶点到3号顶点的路程即dis[3]，通过2->3这条边松弛成功。

这便是Dijkstra算法的主要思想：通过“边”来松弛1号顶点到其余各个顶点的路程。

同理通过2->4（e[2][4]），可以将dis[4]的值从∞松弛为4（dis[4]初始为∞，dis[2]+e[2][4]=1+3=4，dis[4]>dis[2]+e[2][4]，因此dis[4]要更新为4）。

刚才我们对2号顶点所有的出边进行了松弛。松弛完毕之后dis数组为： 
 
接下来，继续在剩下的3、4、5和6号顶点中，选出离1号顶点最近的顶点。通过上面更新过dis数组，当前离1号顶点最近是4号顶点。此时，dis[4]的值已经从“估计值”变为了“确定值”。下面继续对4号顶点的所有出边（4->3，4->5和4->6）用刚才的方法进行松弛。松弛完毕之后dis数组为： 
 
继续在剩下的3、5和6号顶点中，选出离1号顶点最近的顶点，这次选择3号顶点。此时，dis[3]的值已经从“估计值”变为了“确定值”。对3号顶点的所有出边（3->5）进行松弛。松弛完毕之后dis数组为： 
 
继续在剩下的5和6号顶点中，选出离1号顶点最近的顶点，这次选择5号顶点。此时，dis[5]的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边（5->4）进行松弛。松弛完毕之后dis数组为： 
 
最后对6号顶点所有点出边进行松弛。因为这个例子中6号顶点没有出边，因此不用处理。到此，dis数组中所有的值都已经从“估计值”变为了“确定值”。 
最终dis数组如下，这便是1号顶点到其余各个顶点的最短路径。 
 
总结一下刚才的算法。算法的基本思想是：每次找到离源点（上面例子的源点就是1号顶点）最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。基本步骤如下：

1. 将所有的顶点分为两部分：已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始，已知最短路径的顶点集合P中只有源点s一个顶点。我们这里用一个book[ i ]数组来记录哪些点在集合P中。例如对于某个顶点i，如果book[ i ]为1则表示这个顶点在集合P中，如果book[ i ]为0则表示这个顶点在集合Q中。
2. 设置源点s到自己的最短路径为0即dis=0。若存在源点有能直接到达的顶点i，则把dis[ i ]设为e[s][ i ]。同时把所有其它（即源点不能直接到达的）顶点的最短路径为设为∞。
3. 在Q中选择一个离源点s最近的顶点u（即dis[u]最小）加入到P中。并考察所有以点u为起点的边，对每一条边进行松弛操作。
4. 重复第3步，如果集合Q为空，算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。

算法的实现代码如下：

int main() {
    int n,m,s,t;//分别是节点数、边的条数、起点、终点
    while(cin>>n>>m>>s>>t) {
        vector> edge(n+1,vector(n+1,0));//邻接矩阵
        vector dis(n+1,0);//从起点出发的最短路径
        vector book(n+1,0);//某结点已经被访问过

        for(int i=1;i<=n;i++)//初始化邻接矩阵
            for(int j=1;j<=n;j++)
                if(i!=j) edge[i][j]=INT_MAX;

        int u,v,length;
        for(int i=0;i>u>>v>>length;
            if(length dis[index]+edge[index][i]) 
                    dis[i] = dis[index]+edge[index][i];
            }

        }
        cout<

通过上面的代码我们可以看出，这个算法的时间复杂度是O(N2)。其中每次找到离1号顶点最近的顶点的时间复杂度是O(N)。

3. 如何记录最短路径

如果我们需要将那条最短路径记录下来，就要用到一个新数组pre[]，在更新最短路径时，将当前节点的前一个节点记录下来，这样，当最终确定最短路径后，从后往前依次查看pre数组，就可以得到到达当前节点的最短路径了。

 

 

Bellman-Ford算法

1. 定义概览

Bellman-Ford算法是从DJ算法引申出来的，它可以解决带有负权边的最短路径问题。值得注意的是，DJ算法和下面的Floyd算法是基于邻接矩阵的，而Bellman-Ford算法是基于邻接表，从边的角度考量的。

2. 算法描述

Bellman-Ford算法用一句话概括就是：对所有的边进行n-1次松弛操作。如果图中存在最短路径（即不存在负权回路），那么最短路径所包含的边最多为n-1条，也就是不可能包含回路。因为如果存在正回路，该路径就不是最短的，而如果存在负回路，就压根就不存在所谓的最短路径。

---

这里，和用邻接矩阵表示图的方式不同，采用了u、v、w三个矩阵存储边的信息。例如第i条边（有向边）存储在u[i]、v[i]、w[i]中，表示从顶点u[i]到v[i]这条边（u[i]->v[i]）的权值为w[i]。 
之所以把dis[i]初始化为inf，可以理解成，初始时：从1号顶点通过0条边到达其他顶点的路径为正无穷。

int main() {
    int n,m,s,t;//分别是节点数、边的条数、起点、终点
    while(cin>>n>>m>>s>>t) {
        vector u(2*m+1,0);//某条边的起点
        vector v(2*m+1,0);//某条边的终点
        vector length(2*m+1,0);//某条边的长度
        vector dis(n+1,0);//从起点出发的最短路径
        int num=0;
        for(int i=1;i<=m;i++) {//读入每条边
            num++;
            cin>>u[num]>>v[num]>>length[num];
            swap(u[num],v[num]);
        }
        for(int i=num+1;i<=2*num;i++) { //因为是无向图，所以每条边再复制一次，端点交换
            u[i]=v[i-num];
            v[i]=u[i-num];
            length[i]=length[i-num];
        }
        num=2*num;

        for(int i=1;i<=n;i++)//初始化dis数组
            dis[i]=INT_MAX;
        dis[s]=0;

        for(int k=1;k dis[u[j]]+length[j])
                    dis[v[j]] = dis[u[j]]+length[j];
            }

        cout<

•  

对所有m条边进行（n-1）轮松弛，第1轮的效果是得到从1号顶点“只经过一条边”到达其余各顶点的最短路径长度，第2轮则是得到从1号顶点“经过最多两条边”到达其余各顶点的最短路径长度，第k轮则是得到从1号顶点“经过最多k条边”到达其余各顶点的最短路径长度。

 

 

SPFA算法

求单源最短路的SPFA算法的全称是：Shortest Path Faster Algorithm。 很多时候，给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便派上用场了。有人称spfa算法是最短路的万能算法。

算法思想

设立一个队列q用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止。 
松弛操作的原理是著名的定理：“三角形两边之和大于第三边”，在信息学中我们叫它三角不等式。所谓对结点i,j进行松弛，就是判定是否dis[j]>dis[i]+w[i,j]，如果该式成立则将dis[j]减小到dis[i]+w[i,j]，否则不动。 
下面举一个实例来说明SFFA算法是怎样进行的：

和BFS的区别

SPFA在形式上和广度优先搜索非常类似，不同的是BFS中一个点出了队列就不可能重新进入队列，但是SPFA中一个点可能在出队列之后再次被放入队列，也就是一个点改进过其它的点之后，过了一段时间可能本身被改进(重新入队)，于是再次用来改进其它的点，这样反复迭代下去。

代码实现

int main() {
    int n,m,s,t;//分别是节点数、边的条数、起点、终点

    while(cin>>n>>m>>s>>t) {
        vector> edge(n+1,vector(n+1,0));//邻接矩阵
        vector dis(n+1,INT_MAX);//从起点出发的最短路径
        vector book(n+1,0);//某结点在队列中
        queue q;

        for(int i=1;i<=n;i++)//初始化邻接矩阵
            for(int j=1;j<=n;j++)
                if(i!=j) edge[i][j]=INT_MAX;

        int u,v,length;
        for(int i=0;i>u>>v>>length;
            if(lengthdis[top]+edge[top][i]) {
                    dis[i]= dis[top]+edge[top][i]; //更新最短路径
                    if(book[i]==0) { //如果扩展结点i不在队列中，入队
                        book[i]=1;
                        q.push(i);
                    }
                }
            }

        }
        cout<

如何输出最短路径

在一个图中，我们仅仅知道结点A到结点E的最短路径长度，有时候意义不大。这个图如果是地图的模型的话，在算出最短路径长度后，我们总要说明“怎么走”才算真正解决了问题。如何在计算过程中记录下来最短路径是怎么走的，并在最后将它输出呢？ 
我们定义一个path[]数组，path[i]表示源点s到i的最短路程中，结点i之前的结点的编号(父结点)，我们在借助结点u对结点v松弛的同时，标记下path[v]=u，记录的工作就完成了。 
如何输出呢？我们记录的是每个点前面的点是什么，输出却要从最前面到后面输出，这很好办，递归就可以了：

void printpath(int k){
    if (path[k]!=0) printpath(path[k]);
    cout << k << ' ';
}

•  

 

 

Floyd算法

1.定义概览

Floyd算法（弗洛伊德算法）是解决任意两点间的最短路径的一种算法，可以正确处理有向（无向）图的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd算法的时间复杂度为O(N3)，空间复杂度为O(N2)。

2.算法描述

1)算法思想原理

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释。 
从任意节点i到任意节点j的最短路径不外乎2种可能，一是直接从i到j，二是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

2).算法描述

用一个数组来存储任意两个点之间的距离，注意，这里可以是有向的，也可以是无向的。 
 
当任意两点之间不允许经过第三个点时，这些城市之间最短路程就是初始路程。 
如果现在只允许经过1号顶点，求任意两点之间的最短路程，应该如何求呢？只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点，再从1号顶点到j号顶点的路程之和。其中i是1~n循环，j也是1~n循环，代码实现如下。

for(i=1;i<=n;i++) {   
    for(j=1;j<=n;j++) {   
        if ( e[i][j] > e[i][1]+e[1][j] )   
            e[i][j] = e[i][1]+e[1][j];   
    }   
} 

•  

在只允许经过1号顶点的情况下，任意两点之间的最短路程更新为： 
 
通过上图我们发现：在只通过1号顶点中转的情况下，3号顶点到2号顶点（e[3][2]）、4号顶点到2号顶点（e[4][2]）以及4号顶点到3号顶点（e[4][3]）的路程都变短了。

接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢？我们需要在只允许经过1号顶点时任意两点的最短路程的结果下，再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小，代码实现为如下：

//经过1号顶点   
for(i=1;i<=n;i++)   
    for(j=1;j<=n;j++)   
        if (e[i][j] > e[i][1]+e[1][j])  e[i][j]=e[i][1]+e[1][j];   
//经过2号顶点   
for(i=1;i<=n;i++)   
    for(j=1;j<=n;j++)   
        if (e[i][j] > e[i][2]+e[2][j])  e[i][j]=e[i][2]+e[2][j]; 

•  

在只允许经过1和2号顶点的情况下，任意两点之间的最短路程更新为： 
 
通过上图得知，在相比只允许通过1号顶点进行中转的情况下，这里允许通过1和2号顶点进行中转，使得e[1][3]和e[4][3]的路程变得更短了。

同理，继续在只允许经过1、2和3号顶点进行中转的情况下，求任意两点之间的最短路程。任意两点之间的最短路程更新为： 
 
最后允许通过所有顶点作为中转，任意两点之间最终的最短路程为： 
 
整个算法过程虽然说起来很麻烦，但是代码实现却非常简单，核心代码只有五行：

for(k=1;k<=n;k++)   
    for(i=1;i<=n;i++)   
         for(j=1;j<=n;j++)   
             if(e[i][j]>e[i][k]+e[k][j])   
                 e[i][j]=e[i][k]+e[k][j]; 

•  

这段代码的基本思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。下面给出这个算法的完整代码：

int main() {
    int n,m;
    while(cin>>n>>m) {
        vector> edge(n+1,vector(n+1,0));

        for(int i=1;i<=n;i++)//初始化邻接矩阵
            for(int j=1;j<=n;j++)
                if(i!=j) edge[i][j]=INT_MAX;

        int u,v,length;
        for(int i=0;i>u>>v>>length;
            if(length edge[i][k]+edge[k][j])
                        edge[i][j] = edge[i][k]+edge[k][j];

        for(int i=1;i<=n;i++) {//输出最终的邻接矩阵
                for(int j=1;j<=n;j++) 
                    cout<

•  

通过这种方法我们可以求出任意两个点之间最短路径。它的时间复杂度是O(N3)。令人很震撼的是它竟然只有五行代码，实现起来非常容易。正是因为它实现起来非常容易，如果时间复杂度要求不高，使用Floyd算法来求指定两点之间的最短路或者指定一个点到其余各个顶点的最短路径也是可行的。

另外需要注意的是：Floyd-Warshall算法不能解决带有“负权回路”（或者叫“负权环”）的图，因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中，每绕一次1->-2>3这样的环，最短路就会减少1，永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。 

3种算法的比较

适用情况

dj和ford算法用于解决单源最短路径，而floyd算法解决多源最短路径。

dj适用稠密图（邻接矩阵），因为稠密图问题与顶点关系密切； 
ford算法适用稀疏图（邻接表），因为稀疏图问题与边关系密切。 
floyd在稠密图（邻接矩阵）和稀疏图（邻接表）中都可以使用；

PS：dj算法虽然一般用邻接矩阵实现，但也可以用邻接表实现，只不过比较繁琐。而ford算法只能用邻接表实现。

dj算法不能解决含有负权边的图； 
而Floyd算法和Ford算法可以解决含有负权边的问题，但都要求没有总和小于0的负权环路。

SPFA算法可以解决负权边的问题，而且复杂度比Ford低。形式上，它可以看做是dj算法和BFS算法的结合。

3种算法都是既能处理无向图问题，也能处理有向图问题。因为无向图只是有向图的特例，它们只是在邻接矩阵或邻接表的初始化时有所区别。

 

 

补充：A*算法

A*算法把Dijkstra算法（靠近初始点的结点）和BFS算法（靠近目标点的结点）的信息块结合起来。在讨论A*的标准术语中，g(n)表示从初始结点到任意结点n的代价，h(n)表示从结点n到目标点的启发式评估代价（heuristic estimated cost）。当从初始点向目标点移动时，A*权衡这两者。每次进行主循环时，它检查f(n)最小的结点n，其中f(n) = g(n) + h(n)。 
具体的介绍可以见这篇博客： 
链接

(function () {('pre.prettyprint code').each(function () { var lines = numbering = $('

').addClass('pre-numbering').hide(); numbering); for (i = 1; i