机器学习方法篇(11)------SVM入门

● 每周一言

沟通，是解决问题的不二法宝。

导语

支持向量机由Bell实验室于1995年提出，是一种非常有潜力的分类模型。与逻辑回归、神经网络模型相比，支持向量机有着更强的数学理论背景。那么，支持向量机到底是什么？

SVM

支持向量机（Support vector machines，SVM），拆开来看，分成“支持向量”和“机”。“机”在机器学习领域是算法的另一种叫法，比如感知机、波兹曼机等。“支持向量”指的是一些特别的样本，这些样本决定了SVM的模型参数。

我们从一个二维平面的点分类问题入手，具体可以理解为一个有两种特征的数据集二分类问题，比如：房价、面积（两种特征）与是否被购买（样本标签）。

如果使用回归模型，公式为 y = wx + b，其中x为输入二维特征样本，w则是这个二维特征的权重，y和b分别是输出和偏置。模型分类结果如下图红线所示，区分两类样本。

在形式上，SVM也可以用 y = wx + b 表示。但是有别于回归模型，SVM不仅要区分这两类样本，还要使上图红线划分的位置更为合理准确。可想而知，更为合理准确的划分法应该是分割线恰好介于两类最近样本的正中间，这样划分的模型泛化能力最好。

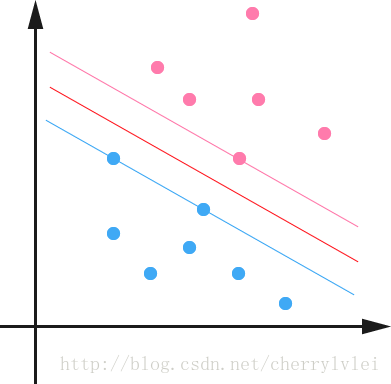
如上图，粉线与红线和蓝线与红线之间的垂直间隔距离相等，即为最优划分。而处于两条边界线上“支撑”这个最优划分的样本，就是上文所说的“支持向量”。

因此，SVM的目标就是最大化这个垂直间隔距离。大家不妨先回忆一下点到直线的距离公式：

上图公式中的直线方程为Ax+By+C=0，点P的坐标为(x0, y0)。回到SVM的公式 y = wx + b，这个距离公式可以写成：

一般情况下SVM中的正负样本标签我们置为1和-1。要最大化上图这个距离，相当于最小化权重向量w的L2范数，如下：

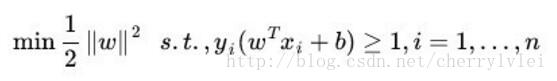
或许你已经看出来了，SVM的整体公式和加了L2正则的线性回归几乎一模一样。的确，我们可以像训练线性回归一样来训练SVM，这对最后的结果不会有任何差异。但是，有着更强数学理论背景的SVM可以有更为高效的训练方法，这个在后面单独一节来讲，敬请期待。

结语

感谢各位的耐心阅读，后续文章于每周日奉上，敬请期待。欢迎大家关注小斗公众号 对半独白！