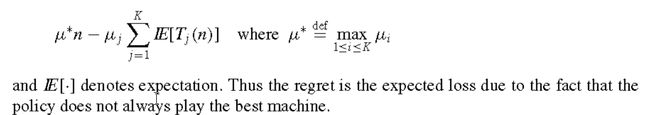强化学习方法（一）：探索-利用困境exploration exploitation，Multi-armed bandit

欢迎转载，转载请注明：本文出自Bin的专栏blog.csdn.net/xbinworld。 技术交流QQ群：433250724，欢迎对算法、技术感兴趣的同学加入。

18年新开一个强化学习方法系列，督促自己能够再不断扩充知识并分享给更多的同学。其实前面写的机器学习方法系列和深度学习方法系列，也都还没有写够，平时工作比较忙，更新很慢，但是我还是会努力更新的。今天开始记录一些强化学习的知识，这些内容以前多少都学习过，但是没有系统地整理成文字，现在权当是再复习一下了。

申明：我写的笔记有参考了很多优秀的网络资源，毕竟我是以整理、分享为目的，并没有任何商业目的；引用的地方我会给出原出处，如有不当请指正。

---

探索-利用困境exploration-exploitation dilemma

强化学习一个非常基础但又非常重要的概念就是探索和利用问题，举个例子来体会一下：

假设你家附近有十个餐馆，到目前为止，你在八家餐馆吃过饭，知道这八家餐馆中最好吃的餐馆可以打8分，剩下的餐馆也许会遇到口味可以打10分的，也可能只有2分，如果为了吃到口味最好的餐馆，下一次吃饭你会去哪里？

所谓探索：是指做你以前从来没有做过的事情，以期望获得更高的回报。所谓利用：是指做你当前知道的能产生最大回报的事情。那么，你到底该去哪家呢？这就是探索-利用困境。

如果你是以每次的期望得分最高，那可能就是一直吃8分那家餐厅；但是你永远突破不了8分，不知道会不会吃到更好吃的口味。所以只有去探索未知的餐厅，才有可能吃到更好吃的，同时带来的风险就是也有可能吃到不和口味的食物。

这个例子只是用于找找感觉，后面会讨论多臂赌博机问题的时候再来多讨论一下。一般基本的最常用的随机策略为 $\epsilon -greedy$策略（抖动策略）：

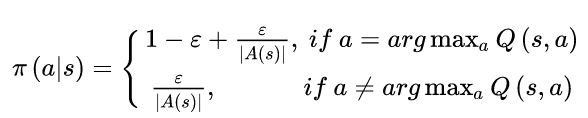
这里我还没有仔细介绍强化学习的基本概念，我想先给一个很初的印象就行。上面s是指当前的状态，a是采取的行动，|A(s)|是指s状态下可以采取行动的总数量，Q是动作值函数，表示对未来奖励的估计。具体在以后讲到基本强化学习方法的时候会再具体解释。这个策略是比贪婪策略稍微复杂一点，意思是说，我会以$\epsilon$概率随机选择任何一个动作，否则选择Q最大的动作。该策略称为抖动策略。

• 利用抖动策略的好处是：
  （1） 抖动策略计算容易，不需要复杂的计算公式。
  （2） 能保证充分探索所有状态。
• 当然相应的坏处是：
  （1） 需要大量探索，数据利用率低。
  （2） 需要无限长时间（取决于状态的数量以及$\epsilon$大小）。

多臂赌博机问题 Multi-armed Bandit Problem##

假设你面前有一排摇臂机，它们的期望回报有差别，显然你希望在最终博弈时尝试胜率更高的那个。多臂赌博机的问题是：你按压哪个臂能得到最大的回报？（以下分析参考[1]）

问题分析：在多臂赌博机问题中，我们有个假设：即按压摇臂后，每个臂获得的回报服从不同的概率分布，在基本问题中，它们的期望是稳定的。比如获得金币的概率是不同的。比如按压摇臂1， 获得金币的概率是0.8；按压摇臂2，获得金币的概率是0.3；按压摇臂3，获得金币的概率是0.6

那么你按压哪个臂能得到最大的回报？很简单：当然选择摇臂1。但是：**问题的难点是你并不知道每个臂获得回报的概率！**那么你该按压哪个臂呢？

这就引出了多臂赌博机的探索-利用困境的问题：刚开始你并不知道哪个臂给出回报的概率大，所以你很可能每个臂都试一试，然后你会记住按压每个臂的结果。根据这些结果，你会粗略的估计每个臂给出回报的概率。假如说你每个臂都按了几次，并观察到按压每个臂时有没有获得回报，那么下一步你该按哪个臂呢？

• 利用（exploitation）: 如果你按压在前几轮中获得回报概率最高的那个臂，这就是你在利用（exploitation）。但是，因为回报是随机的，你对每个臂的回报概率的估计并不准确，或许回报概率最高的那个臂并非当前你用几轮数据估计的那个臂。

• 探索（exploration）：如果你并不去按压在前几轮中获得回报的那个臂，而是继续随机地去按压不同的臂，目的是得到每个臂给出回报更精确的概率估计，从而可能得到真实的那个最优的臂。

现在你只有有限次权限去按压摇臂，为了得到最大的回报，这两种方案你选哪个？
一个折中的策略是：大部分时间你去利用（exploitation），但同时以一定的概率去探索（exploration），这就是探索-利用平衡。现在问题就变成：你应该以多大的概率去利用，以多大的概率去探索呢？

• 策略（policy）：策略是指你怎么选择动作（即你如何选择按压哪个臂。）。
• 有悔（regret）：用来评价策略的好坏。其定义为：你采用一定的策略后获得的回报与最好回报之间的差值。
  

多臂赌博机的问题引起了很多数学家的兴趣。1985年Lai and Robbins在他们的经典书籍《Bandit Problems: sequential allocation of experiments》中给出数学上的证明，存在一个指标策略（index policy）使得该指标策略渐进收敛到最优策略。所谓指标策略就是：你需要根据以往的试验结果对每个臂构建一个指标（或者是一个函数），根据这些指标选择下一个摇臂。

我们可以这样理解，在贪婪策略（exploitation）中, 每个臂的指标是该臂的平均回报。因此其指标策略就是贪婪策略，即选择指标（平均回报）最大的那个臂作为下一次的摇臂。Lai and Robbins 给出证明，渐进收敛的指标策略应该是上确界（UCB）策略。然而，Lai and Robbins并没有给出一个简单的具有一般性的构造上确界函数的方法，1995年，Agrawal在他的论文《Sample mean based index policies with O(logn) regret for the multi-armed bandit problem》中给出了一般的构造指标策略的方法。直到2002年 Peter Auer在他的论文《Finite-time Analysis of the Multiarmed Bandit Problem》提出一个及其简单而被广泛使用的指标策略UCB1策略：

选择所有臂中，指标 ${\bar{x}}_j+\sqrt{\frac{2\ln n}{n_j}}$ 最大的臂作为下一次按压的臂，其中 ${\bar{x}}_j$ 为观测到的第j个臂的平均回报， $n_j$ 为 目前为止按压第j个臂的次数，$n$为到目前为止按压所以臂的次数和。UCB1策略平衡了利用和探索，因为第一项是利用，第二项是探索。UCB1背后的原理是最优化探索。可以证明，采用UCB1策略，Regret的上限是：

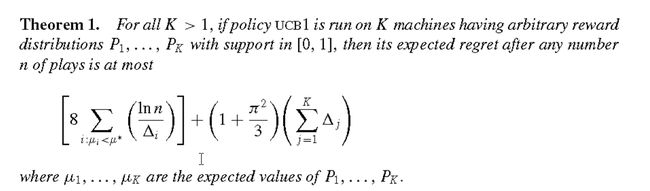
其中${\Delta }_i={\mu }^{\ast }-{\mu }_i$。可以看到，采用UCB1策略，有悔的值随着按压总次数呈对数增长，即$O(\mathbf{l}\mathbf{n}(n))$，而采用常值的探索策略比如前面提到的抖动策略，其有悔的值随按压总次数线性增长，$O(n)$。对数增长啥意思？就是采用UCB1策略，随着摇臂次数线性增长，有悔的增长会越来越缓慢（但还是会一直增长），也就是说获得的回报会更接近最佳回报。

在UCB1的论文中还提到了其他几种UCB策略，以及一种${\epsilon }_n-greedy$ 策略，具体可以参考论文[2]

下面是一个实验，以作示意：

论文实验部分实际上又稍作修改，把UCB1换成了UCB1-tuned，原因是作者发现UCB1-tuned在实验中的表现总是比UCB1好一些，但是作者没法给出UCB1-tuned的regret bound。UCB1-tuned定义如下：

$$\begin{gathered} {\bar{x}}_j+\sqrt{\frac{\ln n}{n_j}}\min \{1/4,V_j(n_j)\} \\ {V}_j(n_j)=\frac{1}{s}\sum _{\tau =1}^s{X}_{j,\tau }^2-{\bar{X}}_{j,s}^2+\sqrt{\frac{2\ln t}{s}} \end{gathered}$$

$V_j(n_j)$as un upper confidence bound for the variance of machine j . As before, this means that machine j , which has been played s times during the first t plays, has a variance that is at most the sample variance plus $\sqrt{\frac{2\ln t}{s}}$.

---

上面介绍的MAB问题以及UCB只是最基本的问题和解法，更详细的发展还有非常多算法，建议参考[3]进行深入阅读，后面我也会在有必要时进行补充解读（工作之余时间太有限了…），本篇入门就先到这里。MAB问题是我觉得非常有趣的一类问题，在现实场景有很多应用。下面若干篇会先介绍一下MCTS和AlphaGo的一些技术知识，让大家对强化学习到底可以做到什么程度有一个了解，然后会回到RL的基本知识从简入深进行算法介绍。

参考资料

[1] 高级强化学习系列 第二讲 探索-利用困境（exploration-exploitation dilemma）
[2] Finite-time Analysis of the Multiarmed Bandit Problem
[3] Bandit Algorithms http://banditalgs.com/
[4] Reinforcement Learning: An Introduction， Richard S. Sutton and Andrew G. Barto