机器学习方法篇(24)------理解RL中的MDP
● 每周一言
珍惜当下,是对未来最好的承诺。
导语
上一节介绍了增强学习的一些基本概念,并提到了增强学习被广泛应用的各种场景。那么,增强学习在这些应用当中到底是如何起作用的?换言之,增强学习的优化目标是什么?
MDP
我们知道, AlphaGo的核心技术是增强学习,我们不妨先仔细想一个问题:对于围棋对弈过程中的每一回合,落子之法究竟受到哪些因素的影响?
抛开人类棋手可能受到的各种情感、心理上的干扰,落子无外乎受到两种因素的影响,就是小斗在上一节基本概念中提到的 状态 和 行为。
状态 指棋面当前的所有落子情况。不难想到,我们无需关心棋面的所有历史落子情况,而只需要关心当前落子情况就行了。
行为 指双方交替落子的动作。同样的,对于行为也只需要关心最近一回合的落子动作,而不用考虑之前的历史落子动作。

对于增强学习只关心最近一次的状态和行为,可以这样理解:好比到商场吃饭,不管你是打车、坐公交,还是步行来到商场门口,对吃点菜还是吃火锅这样的选择不会有任何影响,有影响的只有“进商场吃饭”。
根据上述特点,自然而然可以联想到机器学习中隐马尔可夫模型(Hidden Markov Model,HMM)的无后效性。无后效性的意思是:下个状态只与当前信息有关,而与更早之前的信息无关。
除了HMM,其实马尔科夫模型系列还有其他三兄弟,用状态和动作两方面来划分这四个模型,如下表所示:

增强学习中运用的便是马尔科夫决策过程(Markov Decision Process,MDP)。相比于HMM,MDP不仅考虑状态,还考虑了动作。
增强学习的马尔可夫决策过程通常由一个四元组M = (S, A, Psa, R)构成。S和A分别表示状态和动作;Psa表示状态、动作为s和a的情况下,转移到其他状态的概率;R则表示状态转移的即时奖励。MDP可以用下图表示:
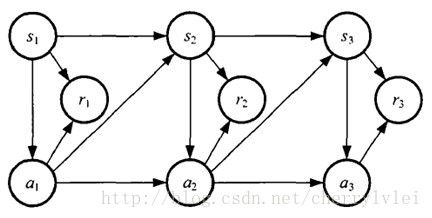
策略函数、价值函数和马尔科夫决策过程都有了,那么究竟怎样的学习叫做增强学习?增强学习的目标又是什么?我们不妨用David Silver的RL公开课经典示例“方格世界”来简单做一次增强学习。
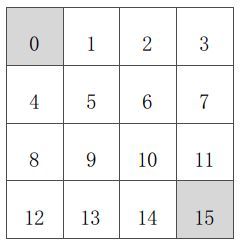
如上图4×4的方格矩阵,已知:
状态空间S:S1 - S14表示非终止状态,S0和S15表示终止状态。
行为空间A:{上,下,左,右} 对于任何一个非终止状态,都可以有上下左右四个移动行为。
转移概率P:越界行为其位置不发生改变,其余行为将100%转移至下一状态。
即时奖励R:在任何非终止状态之间转移得到的即时奖励均为-1,只有进入终止状态的即时奖励为0。
策略函数F:初始策略函数采取随机移动策略,在任一状态下,个体以等概率采取上下左右移动行为。
价值函数V:初始价值函数下,各个状态的价值均为0。
衰减系数γ:定为1,表示上一个状态的价值转移到下一个状态的比例。
问题:求方格世界的最优移动策略。

第一次接触这类问题,大家可能不太容易弄明白怎样才算最优,因为上述的移动并未给出起始点和终止点。其实,这里所谓的最优移动策略,就是不管处于哪一个状态,都能有最优移动方案。
通常情况下,价值驱动策略,即每一次的移动都希望是价值最大的移动。而各个状态的初始价值都一样,这说明这个价值函数一定存在一个迭代计算的过程。然后,收敛好的价值函数又能帮助策略函数改进移动策略。
这样,价值函数和策略函数相互学习调整,便得到了最优的移动策略。价值函数迭代计算过程如下图所示:

由于示例较为简单,迭代到第3轮的价值函数就已经可以推出最优的策略函数了。最优策略函数(图中箭头所示)以及最终价值函数下各个状态的价值如下图:

上述价值函数最终迭代至收敛的次数为153次。至此,我们便知道了增强学习的目标,在给定初始条件下,求解使价值函数V值最大的策略函数F。
以上便是MDP以及增强学习简明执行过程的讲解,敬请期待下节内容。
结语
感谢各位的耐心阅读,后续文章于每周日奉上,敬请期待。欢迎大家关注小斗公众号 对半独白!
