NetworkX玩一下 [email protected]
写在前面的话
She is compelling,spectral, fascinating, an unforgettably unique performer
在写NetworkX的时候我想起来一个梗,一个叫stromezhang的同学,忘了在哪里工作,负责Android的某个APP的开发,是那个项目的头头。很久以前看的,招聘,然后招聘的是iSO 的开发人员。然后把iOS 写成了IOS以及ios的同学的简历全部都挂了,对,挂了!按照他的说法,这是官方的说法,Android,以及android 着两个写法都是有的。但是iOS 这个,苹果公司开发的所有的东西,iPad,iPhone 都是小写。所以,按照这个哥们的说法,我们应该要尊重以及注意所有的细节。
呐,所以既然要对付各种挑剔的朋友,所以我决定严格按照官网上的写法NetworkX
今天,玩一下图。
NetworkX是用Python编写的
官网连接: http://networkx.readthedocs.io/en/networkx-1.10/#
https://networkx.github.io/
1. 创建图
创建一个空图,没有节点没有边。
>>> import networkx as nx
>>> G=nx.Graph()根据定义,图是一系列的点和对应的点对(可以叫做边,或者连接的几何等等)的集合。
在NetworkX 中,节点可以是任何可以Hash的对象,例如,一个文本字符串,一张图片,一个XML的对象,或者是另一个图,或者是一个定制的节点对象
2. 节点
增加一个节点
>>> G.add_node(1)增加一系列的节点
>>> G.add_nodes_from([2,3])或者是增加nbunch的节点。一个nbunch是任何可以迭代的节点的容器,不是一个图中的任何节点。 比如可以是 一个 list(列表),集合(set),一个图(graph),一个文件(file)等等。
>>> H=nx.path_graph(10)
>>> G.add_nodes_from(H)我们可以得到的图如下面所示:
这个是把H这个里面的图的所有点当做每一个点来处理,当然我们可以把H这个里面的所有点当做一个点来处理。
>>> G.add_node(H)3. 边
我们的图同样可以通过增加边来扩大。
我们一次增加一条边。
>>> G.add_edge(1,2)
>>> e=(2,3)
>>> G.add_edge(*e) # unpack edge tuple*我们在增加了这两条边之后我们看看我们的图最后成了什么样子。
通过增加一系列的边
>>> G.add_edges_from([(1,2),(1,3)])或者我们也可以增加任何ebranch 的边。一个ebunch 的边是任何的边的元组的可以迭代的容器。一个边的元组可以是两个节点的元组也可以是一个三元组,跟着一个边的属性。例如:(2,3,{‘weight’:3.1415}) 。边的属性我们将在下面详细讨论。
>>> G.add_edges_from(H.edges())我们可以销毁一个图用下面的一些类似的方法:
Graph.remove_node()
Graph.remove_nodes_from()
Graph.remove_edge()
Graph.remove_edges_from()
我们来试一下效果:
首先我们先将H作为我们的一个点添加进去,然后我们删除这个点H
In [109]: G.add_node(H)
In [110]: nx.draw(G)
In [111]: plt.show()
这个时候我们删除掉我们的H点
G.remove_node(H)显示出删除掉这个点之后的图形
代码:
G.remove_node(H)
nx.draw(G)
plt.show()
我们要删除掉整个图,可以用下面这个方法:
>>> G.clear()用上面这个方法我们可以快速的移除掉所有的边所有的节点
这个时候我们可以快速增加的新的边,新的节点。 并且NetworkX会忽略已经存在的节点。
如下所示:
>>> G.add_edges_from([(1,2),(1,3)])
>>> G.add_node(1)
>>> G.add_edge(1,2)
>>> G.add_node("spam") # adds node "spam"我们可以看第一个语句,已经增加了两条边,1~2 和1~3 。这个时候我们已经加入了三个节点,这个时候我们在加入节点1和我们的边的1—2 之前加入的节点和边会被覆盖或者说是忽略。
这个时候我们在加入一个顶点进去。这个点叫做“spam”
我们来看一下这个图会变成什么样子
这个时候我们加入一系列的点
>>> G.add_nodes_from("spam") # adds 4 nodes: 's', 'p', 'a', 'm'这个阶段我们的图有8个顶点和2条边组成
>>> G.number_of_nodes()
8
>>> G.number_of_edges()
2我们可以检测一下:
>>> G.nodes()
['a', 1, 2, 3, 'spam', 'm', 'p', 's']
>>> G.edges()
[(1, 2), (1, 3)]
>>> G.neighbors(1)
[2, 3]4. 画图
对于NetworkX 也提供了画图的接口Matplotlib 详细的画图教程可以参考 Drawing
为了要画图我们必须要引入Matplotlib’s plot (pylab同样是起作用的)
import matplotlib.pyplot as plt我们可以用下面的任意的一种方法来画这个图:
>>> nx.draw(G)
>>> nx.draw_random(G)
>>> nx.draw_circular(G)
>>> nx.draw_spectral(G)为了让这个图展示出来,我们需要下面这个语句:
>>> plt.show()保存你画的图可以用下面这个语句:
>>> nx.draw(G)
>>> plt.savefig("path.png")下面我们来创建一个图:
In [7]: import networkx as nx
In [8]: G1=nx.Graph()
In [9]: G1.add_edge(0,1)
In [10]: G1.add_edge(0,2)
In [11]: G1.add_edge(0,3)
把这个图画出来:
In [26]: import matplotlib.pyplot as plt
In [27]: nx.draw(G1)
In [28]: plt.show()
这个时候我们来查看一下我们得到的图形,如下所示:
这个时候如果我们想要把这个图形保存为一个dot的文件,我们按照官网上的方法试一下:
>>> from networkx.drawing.nx_pydot import write_dot
>>> nx.draw_graphviz(G)但是出现了 AttributeError: ‘module’ object has no attribute ‘graphviz_layout’ 的提示
我以为是我没有安装 python-pygraphviz
然后我安装了一下:
sudo apt-get update
sudo apt-get install python-pygraphviz可是依然报错。这个时候我把这个包引入进来,可是还是报错
何以解忧,唯有Google:
这个时候找到了解决办法:
http://stackoverflow.com/questions/35279733/what-could-cause-networkx-pygraphviz-to-work-fine-alone-but-not-together
所以说下面我们要讲的是正解
import networkx as nx
from networkx.drawing.nx_agraph import graphviz_layout
from networkx.drawing.nx_pydot import write_dot
pos = graphviz_layout(G1)
nx.draw(G1, pos)
nx.drawing.nx_agraph.write_dot(G1,"graph.dot")这个时候我们就可以得到我们graph.dot 里面的内容
strict graph {
0 -- 1;
0 -- 2;
0 -- 3;
}5. VF2 算法和图同构以及子图同构问题
我们先创建两个图
In [7]: import networkx as nx
In [8]: G1=nx.Graph()
In [9]: G1.add_edge(0,1)
In [10]: G1.add_edge(0,2)
In [11]: G1.add_edge(0,3)
In [12]: G2=nx.Graph()
In [13]: G2.add_edge(0,1)
In [14]: G2.add_edge(0,2)
In [15]: G2.add_edge(0,3)
In [16]: G2.add_edge(0,4)
In [17]: G2.add_edge(0,5)
之后我们来判断这两个图是不是同构:
from networkx.algorithms import isomorphism
GM = isomorphism.GraphMatcher(G2,G1)
GM.subgraph_is_isomorphic()
GM1 = isomorphism.GraphMatcher(G1,G2)
GM1.subgraph_is_isomorphic()我们来看一下它的执行效果:
第一个结果返回的是真的,第二个结果返回的结果是假
图1
图2
因为我们的函数:
GraphMatcher.subgraph_is_isomorphic()
Returns True if a subgraph of G1 is isomorp在两个图比较的时候,当且仅当G2中的一个子图和G1是同构的
所以至少G2的节点要大于等于G1才有子图同构的可能。
如果我们想查看我们比较的两个图当中哪一些是结点是同构的我们可以使用
GM.mapping 来查看
用mapping 函数我们得到的是一个字典的结构我们可以看一下匹配的结点数目总共是4.
完整的代码如下所示:
In [1]: import os
In [2]: import networkx as nx
In [3]: G1= nx.Graph()
In [4]: G1
Out[4]: .classes.graph.Graph at 0x7fc704be8510>
In [5]: import matplotlib.pyplot as plt
In [6]: G1.add_edge(0,1)
In [7]: G1.add_edge(0,2)
In [8]: G1.add_edge(0,3)
In [9]: nx.draw(G1)
In [10]: plt.show()
In [11]: G2 = nx.Graph()
In [12]: Gx.add_edge(0,1)
In [13]: G2.add_edge(0,1)
In [14]: G2.add_edge(0,2)
In [15]: G2.add_edge(0,3)
In [16]: G2.add_edge(0,4)
In [17]: G2.add_edge(0,5)
In [18]: G2.add_edge(3,6)
In [19]: G2.add_edge(4,7)
In [20]: G2.add_edge(4,8)
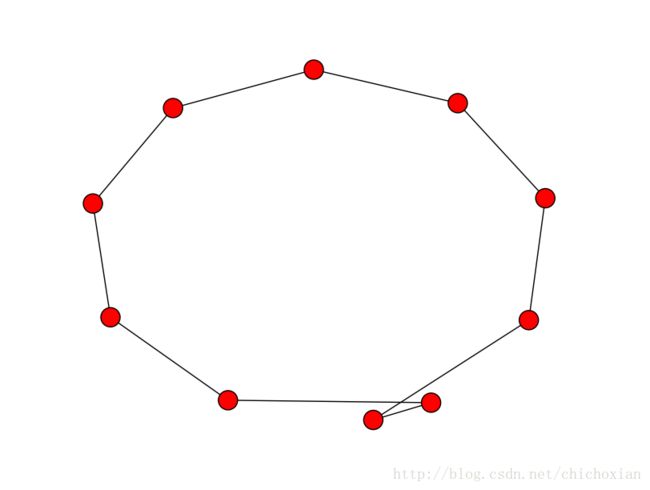
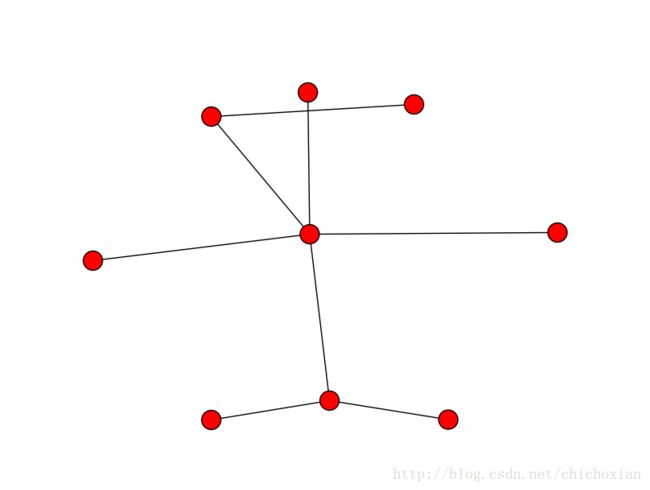
In [21]: nx.draw(G2)
In [22]: plt.show()
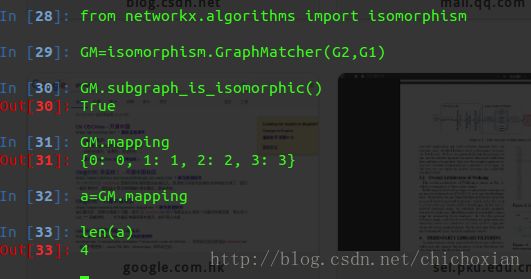
In [28]: from networkx.algorithms import isomorphism
In [29]: GM=isomorphism.GraphMatcher(G2,G1)
In [30]: GM.subgraph_is_isomorphic()
Out[30]: True
In [31]: GM.mapping
Out[31]: {0: 0, 1: 1, 2: 2, 3: 3}
In [32]: a=GM.mapping
In [33]: len(a)
Out[33]: 4
我们比较的两个图分别是下面这个样子的:
G1
G2
再次申明, 我们在调用函数isomorphism.GraphMatcher的时候 表示的第一个参数的图中存在一个子图,这个子图和我们的第二参数的图是同构的。