stepwise算法

原始的交叉矩阵的q行q列进行sweep变换：

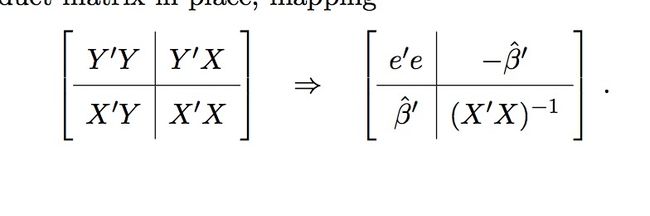
可以看到sweep之后，原本叉乘矩阵的位置变成了它的逆矩阵，而第一行residueSS向量的第0个元素表示的是 RSSq ,剩下的表示的是系数。
如果我们想将q个变量扩充成 q+1 个变量，可以参考下图：

首先将 Z 分解为两部分： Z=Z1+Z2 ,
Z1=(I−H)Z ， Z2=HZ
其中 Z1 表示新加变量 Z 的垂直于 span｛x1,x2,...,xq｝ 分量， Z2 表示新加变量 Z 在 span｛x1,x2,...,xq｝ 上的投影.
可以看到对前面的 q 列sweep之后，记为如下简化形式：
A11=RSSq    A12=−βq        A13=(y−yq)′z1
A21=βq     A22=(X′X)−1      A23=X′z1
A31=z′1(y−yq)     A32=z′1X     A33=z′1z1

（1）我们要记下第一行的所有元素，放到residueSS中，可以看到 A13 放的是当前残差向量在新变量的垂直分量上的投影。
（2） A23 放的是 X 在 z1 上的投影， A32 放的是 z1 在 X 上的投影。
（3） A33 表示垂直分量的长度。

再回到文章中的主要使用算法：也就是下面的代码
`ExpandStepwiseModel(SweepMatrix sm, int nToAdd)//nToAdd表示给已有模型新加进去的变量个数
int nAddedSoFar = 0;
long bestVars[CACHE_UPDATE_SIZE], bestVarToUse;
int i, gotOne;

nToAdd = AdjustNumberToAdd(sm, nToAdd);
while (nAddedSoFar < nToAdd)
{ // this is for hard threshold
/*
Key_sorter::s_threshold =
2.0 * log(((double)NumberOfPossiblePredictors(sm)-(double) sm->qBase));
fprintf (stderr, “SM: Hard threshold F = %6.2f.\n”, Key_sorter::s_threshold);
*/
// This code is the old style adaptive threshold, using white adjusted F
/*
Key_sorter::s_threshold =
2.0 * log( ((double)NumberOfPossiblePredictors(sm)-(double) sm->qBase)/
(1.0 + (double)NumberOfPredictors(sm) - (double) sm->qBase));
fprintf (stderr, “SM: Adaptive threshold F = %7.3f with q base at %d\n”,
Key_sorter::s_threshold,sm->qBase);
*/
// This version does the bennett rss sort

  Key_sorter::s_threshold =//bonferonni阈值
  (1.0 + (double)(NumberOfPredictors(sm) - sm->qBase)) /
  (double)(NumberOfPossiblePredictors(sm)- sm->qBase);

fprintf (stderr, "SM: q/p = %8.6f with q base at %d\n",
     Key_sorter::s_threshold,sm->qBase);

// Mark columns with no variation prior to search
MarkConstantColumns(sm);//开始搜寻下一个变量之前，把已有模型的变量标记为skipped
// Init tree so that have a new tree each time in loop (dont fill old one)
Sort_tree tree;//每一次迭代时。都要初始化一个Sort_tree，用来装未选入变量的ss的排序
FindNextVariables(sm, &tree);//使用sm来寻找下一个变量，并且将排好序的变量放入tree中
fprintf (stderr, "SM: Moving var indices, updating cache.\n");
Sort_tree::iterator treeIt;//初始化Sort_tree的迭代器treeIt
for (i=0, treeIt=tree.begin(); isecond;//second装的是f统计量，fist装的是rss
if (UpdateCache(sm, bestVars, CACHE_UPDATE_SIZE, 0) < 0) return -1;
// Find column with highest partial covariance (starting with last)
// and check that it has a large F stat
fprintf (stderr, "SM: Checking found predictor corr.\n");
treeIt = tree.begin();
Key bestKey = treeIt->first;//选最好的变量带来的
bestVarToUse = treeIt->second;//房产
if (bestKey.second > Key_sorter::s_threshold)//如果最好的
  gotOne = 1;
else gotOne = 0;
if (!gotOne)
  fprintf (stderr, "SM: *** Did not find variable meeting F rule *** \n");
AddCrossProductToSweep(sm, bestVarToUse);
// Sweep out effects from row just added
SweepLastRow(sm);
++nAddedSoFar;
// PrintCurrentFit (sm);

}
return nAddedSoFar;
｝`

bennet不等式：

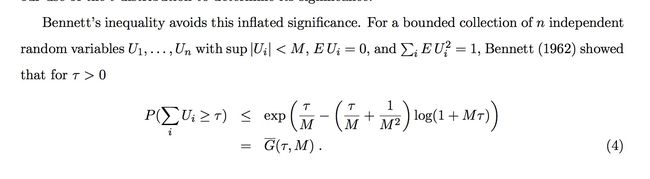
double
bennett_lower_bound (double beta, double a, double b, double pValue)
{
// assert(b > 0);
if (b > 0.0)
{
double m = a/b;
double beta0 = abs_val(beta);
double p = bennett_p_value(beta0/b,m);
if (p > pValue)
return 0.0;
else {
while (bennett_p_value(beta0/b,m) < pValue)
beta0 -= b;
beta0 += .1 * b;
while (bennett_p_value(beta0/b,m) > pValue)
beta0 += .1 * b;
return beta-beta0;
}
}
else
return 0.0;
}

代码中的 t 就是论文中的 τ, ,表示 t 值，代码中的 m 就是 M ，表示这些随机变量的上界。