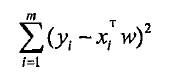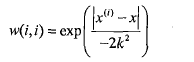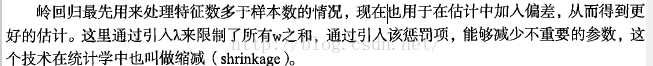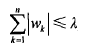《机器学习实战》预测数值型数据-回归（Regression）

本文转载自:http://blog.csdn.net/gamer_gyt/article/details/51405251

1：用线性回归找到最佳拟合曲线

       

    回归的目的是预测数值型的目标值。最直接的办法是依据输人写出一个目标值的计算公式。 假如你想要预测姐姐男友汽车的功率大小，可能会这么计算：

这就是所谓的回归方程，其中的0.0015和-0.99称作为回归系数，求这些回归系数的过程就是回归

回归的一般方法：

（1）收集数据：采用任意方法收集数据

（2）准备数据：回归需要数值型数据，标称型数据将被转化成二值型数据

（3）分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后，可以将新拟合线在图上作为对比

（4）训练算法：求得回归系数

（5）测试算法：使用R2或者预测值和数据的拟合度，来分析模型的效果

（6）使用算法：使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续性数据而不仅仅是离散的类别标签

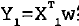
假定输入数据存放在矩阵X中，而回归系数存放在向量w中，那么对于给定的数据X预测结果将会通过  给出，加入在给定数据X和Y的情况下怎么求得W？

误差最小化：

同过找到最小误差求W（误差是真实Y和预测Y之间的差值，使用该误差的简单累加将使得正误差和负误差相互抵消，所有我们采用平方误差）

                                                                     

我们可以通过调用Numpy库的矩阵方法求得w，即所谓最小二乘法（OLS）

代码实现

 #-*-coding:utf-8-*-
 '''''
 Created on 2016年5月14日

 @author: Gamer Think
 '''

 from numpy import *

 #====================用线性回归找到最佳拟合曲线===========
 #加载数据集
 def loadDataSet(filename):
     numFeat = len(open(filename).readline().split("\t")) -1
     dataMat = []; labelMat = []
     fr = open(filename)
     for line in fr.readlines():
         lineArr = []
         curLine = line.strip().split("\t")
         for i in range(numFeat):
             lineArr.append(float(curLine[i]))

         dataMat.append(lineArr)
         labelMat.append(float(curLine[-1]))

     return dataMat,labelMat

 #计算最佳拟合曲线
 def standRegress(xArr,yArr):
     xMat = mat(xArr); yMat = mat(yArr).T  #.T代表转置矩阵
     xTx = xMat.T * xMat
     if linalg.det(xTx) ==0.0: #linalg.det(xTx) 计算行列式的值
         print "This matrix is singular , cannot do inverse"
         return
     ws = xTx.I * (xMat.T * yMat)
     return ws

 #测试上边的函数
 xArr,yArr = loadDataSet("ex0.txt")
 ws = standRegress(xArr, yArr)
 print "ws（相关系数）：",ws    #ws 存放的就是回归系数

 #画图展示
 def show():
     import matplotlib.pyplot as plt
     xMat = mat(xArr); yMat = mat(yArr)
     yHat = xMat*ws
     fig = plt.figure() #创建绘图对象
     ax = fig.add_subplot(111)  #111表示将画布划分为1行2列选择使用从上到下第一块
     #scatter绘制散点图
     ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
     #复制，排序
     xCopy =xMat.copy()
     xCopy.sort(0)
     yHat = xCopy * ws
     #plot画线
     ax.plot(xCopy[:,1],yHat)
     plt.show()

 show()

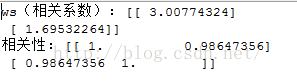
 #利用numpy库提供的corrcoef来计算预测值和真实值得相关性
 yHat = mat(xArr) * ws  #yHat = xMat * ws
 print "相关性：",corrcoef(yHat.T,mat(yArr))
 #====================用线性回归找到最佳拟合曲线===========

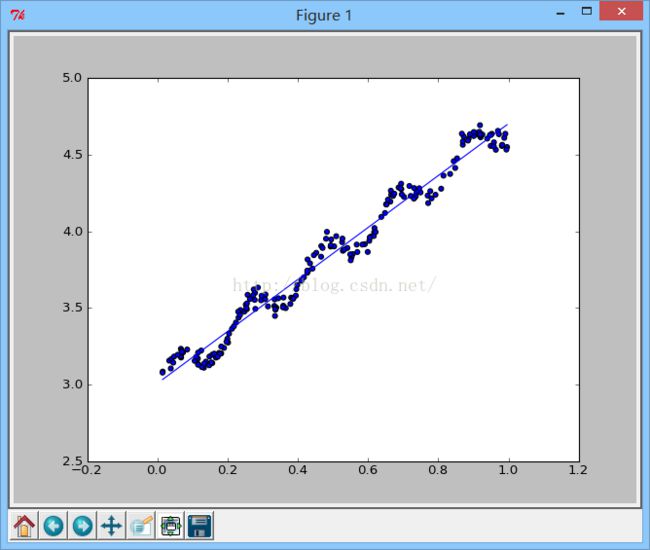
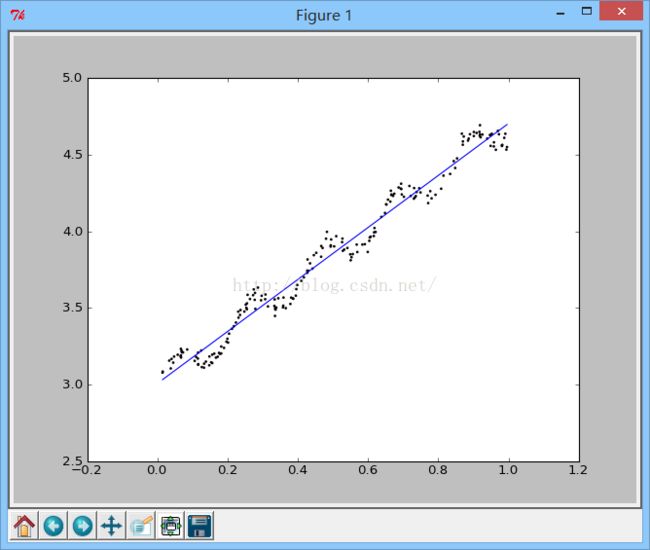
效果展示：

(相关性中对角线1,1表示yHat与自己的匹配是完全的，与yMat的匹配是0.98）

2：局部加权线性回归

       加权的目的：降低预测的均方误差，减小欠拟合现象

       加权方法：局部加权线性回归（Locally Weighted Liner Regression，LWLR）在该算法中，我们给待预测点附近的每个点赋予一定的权重，然后利用上一节的方法计算最小均方差来进行普通的回归

       此时回归系数：

                       

其中W是一个矩阵，用来给每个数据点赋予权重

LWLR使用核来对附近的点赋予更高的权重，最常用的核方法是高斯核，其对应的权重如下：

                         

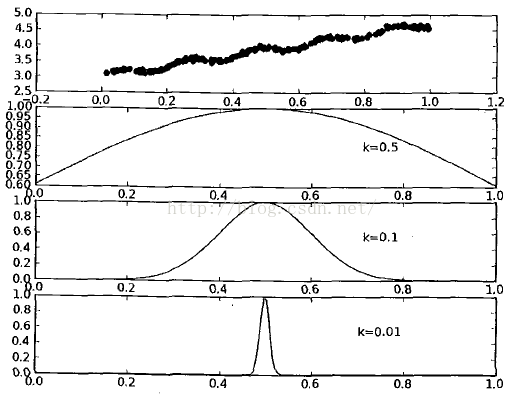
这样就构建了一个只含对角线元素的权重矩阵w，并且点x与x（i）越近，w(i,i)将会越大，上述公式包含一个需要用户指定的参数k，他决定了对附近的点赋予多大的权重，这也是使用LWLR时唯一需要考虑的参数，下图展示了参数k与权重的关系

                           

在regression.py文件中加入以下代码

 #==================局部加权线性回归================

 def lwlr(testPoint,xArr,yArr,k=1.0):
     xMat = mat(xArr); yMat = mat(yArr).T
     m = shape(xMat)[0]
     weights = mat(eye((m)))   #产生对角线矩阵
     for j in range(m):
         diffMat = testPoint - xMat[j,:]
         #更新权重值，以指数级递减
         weights[j,j] = exp(diffMat * diffMat.T /(-2.0*k**2))
     xTx = xMat.T * (weights * xMat)
     if linalg.det(xTx) == 0.0:
         print "this matrix is singular,cannot do inverse"
         return
     ws = xTx.I * (xMat.T * (weights * yMat))
     return testPoint * ws

 def lwlrTest(testArr,xArr,yArr,k=1.0):
     m = shape(testArr)[0]
     yHat = zeros(m)
     for i in range(m):
         yHat[i] =lwlr(testArr[i],xArr,yArr,k)
     return yHat


 xArr,yArr = loadDataSet('ex0.txt')
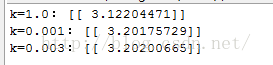
 print "k=1.0：",lwlr(xArr[0],xArr,yArr,1.0)
 print "k=0.001：",lwlr(xArr[0],xArr,yArr,0.001)
 print "k=0.003：",lwlr(xArr[0],xArr,yArr,0.003)

 #画图
 def showlwlr():
     yHat = lwlrTest(xArr, xArr, yArr, 0.003)
     xMat = mat(xArr)
     srtInd = xMat[:,1].argsort(0)
     xSort = xMat[srtInd][:,0,:]

     import matplotlib.pyplot as plt
     fig = plt.figure() #创建绘图对象
     ax = fig.add_subplot(111)  #111表示将画布划分为1行2列选择使用从上到下第一块
     ax.plot(xSort[:,1],yHat[srtInd])
     #scatter绘制散点图
     ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T[:,0].flatten().A[0],s=2,c='red')
     plt.show()

 showlwlr()

运行结果和不同k值得图像比较

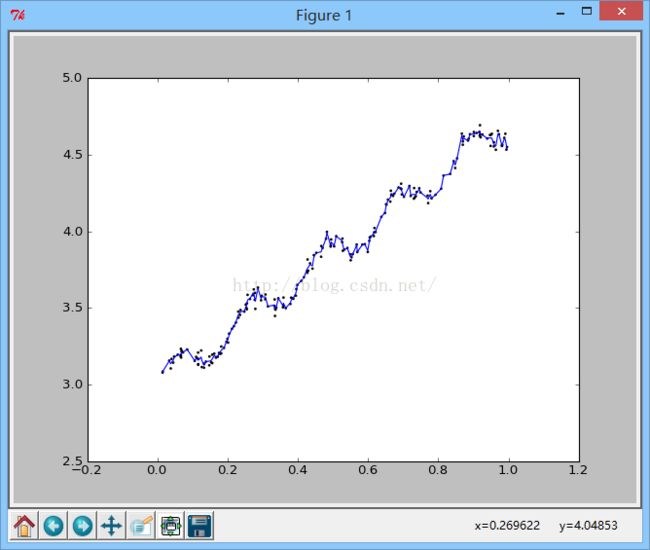
k=0.003时的输出图为：

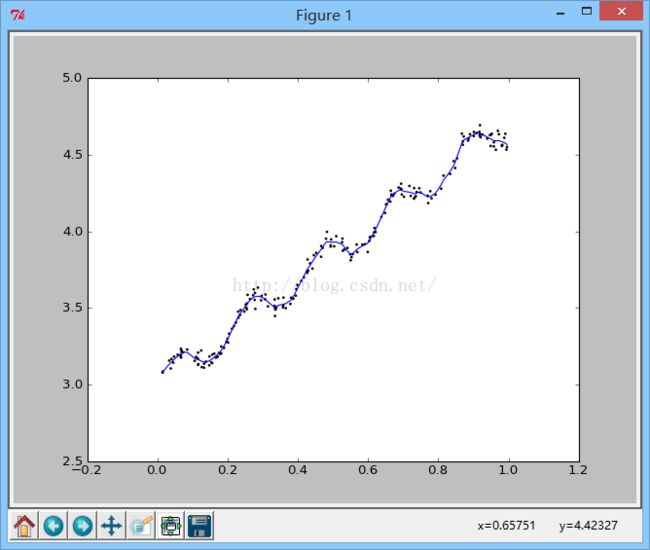
k=0.01时对应的输出图：

k=1.0时的输出图：

从上图可以看出k=0.01时可以得到很好的效果

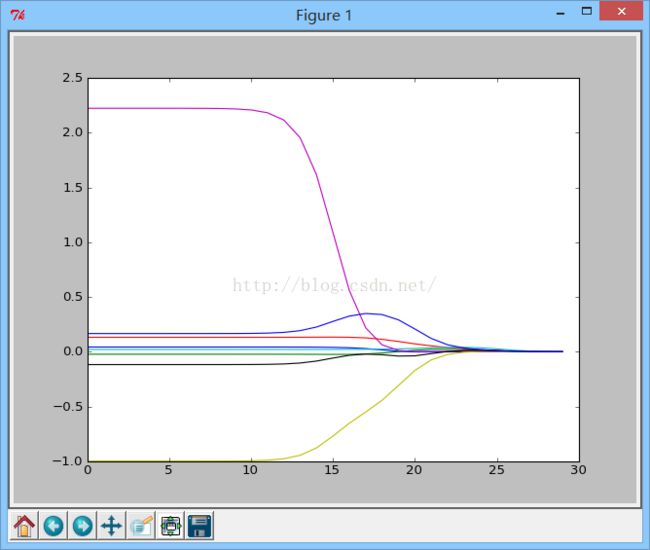
3：缩减系数来“理解”数据

如果系数的特征比样本点还多，在计算（X^t X）^-1 的时候会出错，为了解决这个问题，统计学家引入了岭回归的概念，还有lasso法，该方法效果很好，但是计算复杂，还有另外一种缩减方法称为岭向前逐步回归，可以得到与lasso差不多的效果，且更容易实现。

(1)：岭回归

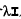
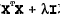岭回归就是在矩阵X^t X 上加一个   从而使得矩阵非奇异，进而能对   求逆，其中矩阵I是一个m*m的单位矩阵，对角线上元素全为1，其他元素全为0，而  是用户定义的数值，后面会做介绍，此时回归系数的计算公式将变为：

                                                       

          

          

缩减方法可以去掉不重要的参数，因此能更好的理解数据，此外，与简单的线性回归相比，缩减法能取得更好的预测效果，在这里依旧采用预测误差最小化得到 ：数据获取之后先抽取一部分用于测试，剩余的作为训练集用于训练数据W。

在regression.py中加入以下代码：

 #=========================岭回归==================
 #用于计算回归系数
 def ridgeRegres(xMat,yMat,lam=0.2):
     xTx = xMat.T * xMat
     denom = xTx + eye(shape(xMat)[1]) * lam
     if linalg.det(denom)==0.0:
         print "This matrix is singular, cannot do inverse"
         return
     ws = denom.I * (xMat.T * yMat)
     return ws

 #用于在一组lambda上做测试
 def ridgeTest(xArr,yArr):
     xMat = mat(xArr); yMat = mat(yArr).T
     yMean = mean(yMat,0)
     #数据标准化
     yMat = yMat - yMean
     xMeans = mean(xMat,0)
     xVar = var(xMat,0)
     xMat = (xMat - xMeans)/xVar

     numTestPts = 30
     wMat = zeros((numTestPts, shape(xMat)[1]))
     for i in range(numTestPts):
         ws = ridgeRegres(xMat, yMat, exp(i-10))
         wMat[i,:]=ws.T
     return wMat

 abX,abY = loadDataSet('abalone.txt')
 ridgeWeights = ridgeTest(abX,abY)
 # print ridgeWeights

 def showRidge():
     import matplotlib.pyplot as plt
     fig = plt.figure()
     ax = fig.add_subplot(111)
     ax.plot(ridgeWeights)
     plt.show()

 showRidge()
 #===================岭回归=============

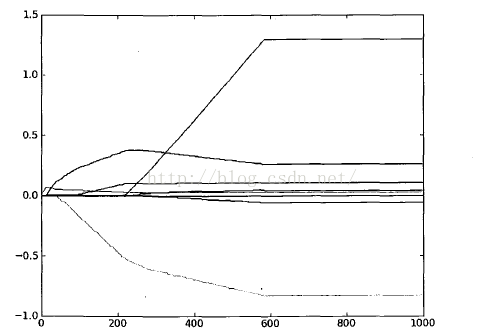
运行结果：

说明：lambda非常小时，系数与普通回归一样，而lambda非常大时，所有回归系数缩减为0，可以在中间某处找到使得预测结果最好的值

（2）：lasso

不难证明，在增加如下约束时，普通的最小二乘法回归会得到与岭回归的一样的公式：

                                            

上式限定了所有的回归系数的平方和不能大于lambda，使用普通的最小二乘法回归在当两个或更多的特征相关时，可能会得到一个很大的正系数和一个很大的负系数。正是因为上述限制条件的存在，使用岭回归可以避免这个问题

与岭回归类似，另外一个缩减方法lasso也对回归系数做了限定，对应的约束条件是如下：

                                                 

唯一一点不同的是这个约束条件使用绝对值取代了平方和，虽然约束条件只是稍作变化，结果却大相径庭，在lambda足够小的时候，一些系数会因此被迫缩减到0，而这个特性可以帮助我们更好的理解数据，这两个约束条件虽然相差无几，，但细微的变化却极大的增加了计算的复杂度，下面介绍一种更为简单的方法来得到计算结果，该方法叫做向前逐步回归

（3）：向前逐步回归

向前逐步回归算法可以得到和lasso差不多的效果，但是更加简单，它属于一种贪心算法，即每一步都尽可能的减小误差，一开始，所有的权重都设为1，然后每一步所做的决策是对某个权重增加或者减小一个很小的值

该算法的伪代码如下：

数据标准化，使其分布满足0均值和单位方差

在每轮迭代过程中：

        设置当前最小误差lowestError为正无穷

        对每个特征：

                增大或减小：

                        改变一个系数得到一个新的W

                        计算新W下的误差

                        如果误差Error小于当前最小误差lowerError：设置Wbest等于当前的W

                将W设置为新的Wbest

代码实现如下

 #===================向前逐步回归============

 #计算平方误差
 def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
     return ((yArr-yHatArr)**2).sum()

 #数据标准化处理
 def regularize(xMat):#regularize by columns
     inMat = xMat.copy()
     inMeans = mean(inMat,0)   #calc mean then subtract it off
     inVar = var(inMat,0)      #calc variance of Xi then divide by it
     inMat = (inMat - inMeans)/inVar
     return inMat


 def stageWise(xArr,yArr,eps=0.01,numIt=100):
     xMat = mat(xArr); yMat=mat(yArr).T
     yMean = mean(yMat,0)
     yMat = yMat - yMean     #can also regularize ys but will get smaller coef
     xMat = regularize(xMat)
     m,n=shape(xMat)
     returnMat = zeros((numIt,n)) #testing code remove
     ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
     for i in range(numIt):#could change this to while loop
         #print ws.T
         lowestError = inf;
         for j in range(n):
             for sign in [-1,1]:
                 wsTest = ws.copy()
                 wsTest[j] += eps*sign
                 yTest = xMat*wsTest
                 rssE = rssError(yMat.A,yTest.A)
                 if rssE < lowestError:
                     lowestError = rssE
                     wsMax = wsTest
         ws = wsMax.copy()
         returnMat[i,:]=ws.T
     return returnMat

 xArr,yArr = loadDataSet('abalone.txt')
 print stageWise(xArr, yArr, 0.01, 200)

运行结果：

上述结果中值得注意的是wl和w6都是0 ,这表明它们不对目标值造成任何影响，也就是说这 些特征很可能是不需要的。另外，在参数eps设置为0.01的情况下，一段时间后系数就已经饱和 并在特定值之间来回震荡，这是因为步长太大的缘故。这里会看到，第一个权重在0.04和0.05之 间来回震荡。

设置更小的步长：

print stageWise(xArr, yArr, 0.001, 200)

接下来把这些结果与最小二乘法进行比较，后者的结果可以通过如下代码获得

 xMat = mat(xArr)
 yMat = mat(yArr).T
 xMat = regularize(xMat)
 yM = mean(yMat,0)
 yMat = yMat - yM
 weights = standRegress(xMat, yMat.T)
 print weights.T

可以看出在迭代5000次以后，逐步线性回归算法与常规的最小二乘法类似，使用0.005的epsilon值并经过1000次迭代后的结果参见

逐步线性回归算法的实际好处并不在于能绘出图8-7这样漂亮的图’ 主要的优点在于它可以帮助人们理解现有的模型并做出改进。当构建了一个模型后，可以运行该算法找出重要的特征，这样就有可能及时停止对那些不重要特征的收集。最后，如果用于测试，该算法每100次迭代后就可以构建出一个 模型，可以使用类似于10折交叉验证的方法比较这些模型，最终选择使误差最小的模型。当应用缩减方法（如逐步线性回归或岭回归)时，模型也就增加了偏差（础8)，与此同时却减小了模型的方差。