时间序列频繁模式挖掘:GSP算法、SPADE算法
本文核心理论依托于MOHAMMED J. ZAKI于Machine Learning, 42, 31–60, 2001发表的文章,由于国内暂时没有相应文献对SPADE算法做详细讲解,本人翻译原文后以通俗易懂的形式展现给读者。英文水平捉急,若有个别地方理解有误望批评指正。
1.什么是时间戳概念的频繁模式挖掘?
所谓时间戳(time-stamp)就是加入了时间序列的概念,即每次发生的时间都有时间先后的顺序,在前面讲解的Apriori算法中并没有加入此概念,虽然Apriori加入了先验性质以减少每轮遍历的次数,但是由于加入了“时间发生先后”的概念,导致时间复杂度大大增加,无疑需要一种新颖的办法解决该问题。
2.GSP算法
GSP算法是加入了垂直列表数据库和哈希树概念的Apriori算法,并且依旧使用连接步、剪枝步完成计算。其处理思路如下:

上图是我们的原始数据,其中SID表示事件号,EID表示时间戳(即什么时候发生了该动作),我们可以看到,在一个事件内可以在多个时间发生动作,在一个时间点内也可以发生多个动作,诸如x->y这样的行为表示先发生了x,之后发生了y,之间隔了多长时间无所谓,但是一定要在一个SID中。
如果假定支持度为2,那么1成员频繁序列有A、B、D、F四个成员,出现的次数如右图,以成员A为例,则表示A成员在SID=1~4这四个事件中都出现过,在计算2成员频繁序列中采用广度搜索的哈希树作为遍历手段,如下图所示:
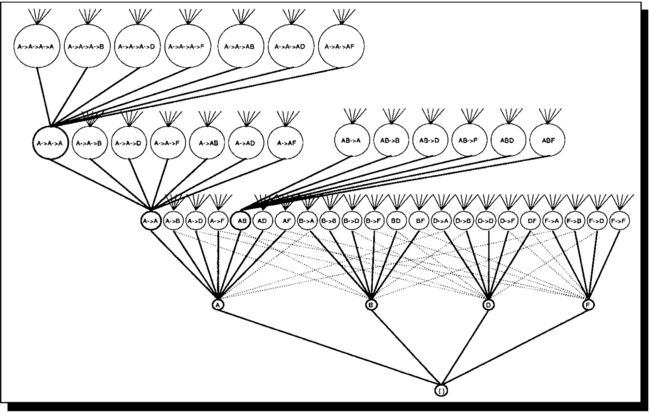
我们可以看到,再加入时间戳概念后,遍历的复杂度大大提高,因为不光要考虑诸如AB这样的“同时发生”的概念,概要考虑A->B这样的先后次序发生概念,在本data中寻找2成员频繁项集一共需要(3*2)*4=24次,然后每次需要在遍历全部的data来判断该项目是否频繁,那么一共需要计算24*10=240次,几百次对计算机来说不成问题。最终计算结果如下图:
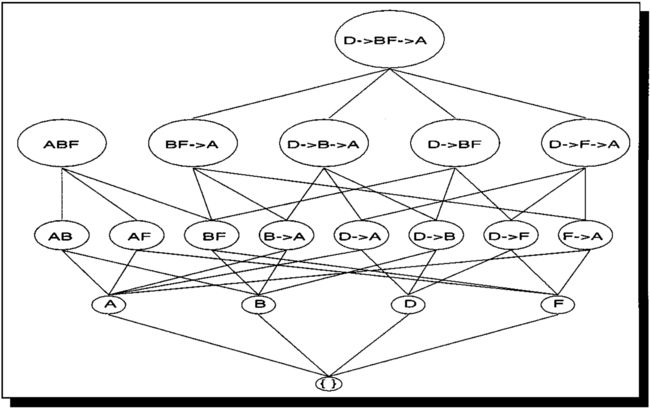
我可以看到,3成员频繁项集虽然看起来匹配的很轻松,但是依旧要遍历8次原始数据,一旦数据巨大,无疑这笔开销会异常恐怖,为了进一步提升效率,学者研发了SPADE算法。
2.SPADE算法
SPADE算法依旧使用传统的先验性质,即连接步+剪枝步的经典组合,思想跟GSP大致相同,其中寻找1成员和2成员频繁项集方法跟GSP完全形同,在之后的3成员及之后的频繁项计算中,采取了一种“作弊”的办法 (= -) ,该办法套用了三种屡试不爽的公式,如下:
1.如果诸如成员PA,PD这样的形式出现在2频繁项集中,则能推导出PBD这样的三成员元素。
2.如果出现诸如PB,P->A这样的形式出现在2频繁项集中,则能推导出PB->A这样的三成员元素。
3.如果出现诸如P->A,P->F这样的形式出现在2频繁项集中,则能推导出P->AF或P->A->F或P->F->A这样的三成员元素。

以上推推导出的三成员元素注意!仅仅是“有可能”是频繁的元素,至于是不是频繁的,还得去原始data中进一步遍历、判断。
比如在本例中AB,AF是两个频繁的2成员项,那么有可能注意是“有可能”存在且仅存在ABF这样的3成员频繁项,经过10次计算遍历了一遍data发现ABF确实是频繁的。
在本例中出现了一组奇葩,即D->F,F->A能推导出D->F->A,看似是非常成立的,但经过我的推导发现不一定成立,这怎么办。。。没办法,遇到这种情况只能遍历data。虽说采用SPADE的秘籍可以减少一定的计算次数,但是我觉得它的精髓在于减少I\O次数,毕竟I\O的时间相比计算的时间长的多得多,同时还能节省内存。
大致思路就是这样,我还没写程序,确实有点难写,网上没有任何源码可供参考,我还是会努力写的,我写好会在下面粘出来。
2015.10.20我终于写完了源码(python),下面粘下来:运行时间0.000791秒
#coding:utf-8
import itertools
import datetime
class GSP(object):
def __init__(self):
self.queue = []
#----------------------------------------------------------#
# 计算freq1 #
#----------------------------------------------------------#
def freq1(self, data, frequent_num):
appear = ''
freq1 = []
appear_ele = []
appear_ele2 = []
for i in range(len(data)):
appear = ''
for j in range(len(data[i])):
appear += data[i][j]
appear_ele += list(set(appear))
# print(appear_ele)
appear_ele2 = list(set(appear_ele))
# print(appear_ele2)
for item in appear_ele2:
itmes = appear_ele.count(item)
if itmes >= frequent_num:
freq1.append(item)
print('频繁1项集为:%s' %freq1)
return freq1
#----------------------------------------------------------#
# 计算freq_more #
#----------------------------------------------------------#
def freq_more(self, data, freq1):
queue = []#所有的备选序列放在这里面
queue_new = []#最终结果在这里面
top = 0 #这个是queue_new的队尾标号
times = 3
while True:
if (queue_new == []): #为空则代表这是第一次遍历,python中的&&是and,||是or
for i in range(len(freq1)):
for j in range(i+1, len(freq1)):
item = freq1[i] + freq1[j]
queue.append(item)
for i in range(len(freq1)):
for j in range(len(freq1)):
if j != i:
item = freq1[i] +'->'+ freq1[j]
queue.append(item)#第一次遍历后全部可能出现的情况
for i in range(len(queue)):
freq_item = self.isFreq(queue[i], data)
if freq_item != 0:
queue_new.append(freq_item)
queue = []#清空queue(备选序列)
if (queue_new != []): #后几次遍历时要把所有的情况写入空的queue中
if top == len(queue_new) - 1: #表示没有新加入元素,那么终止 while 循环
print('频繁多项集为:%s' %queue_new)
break
else:
demo_list = []#专门放'AB','BF','AF'这样的频繁序列,后面将他们合成为更多成员的备选频繁序列
for i in range(top, len(queue_new)):
if '->' not in queue_new[i]:
demo_list.append(queue_new[i])
demo_string = self.List_to_String(demo_list) #将列表中的元素拼接成字符串,诸如拼成'ABBFAF'
demo_ele = "".join(set(demo_string)) #删除串中的重复元素,输出'ABF'
if len(demo_ele) >= times:
if len(demo_ele) == times :#那么demo_ele是唯一的备选成员
queue.append(demo_ele)
times += 1
else: #否则对备选字母进行排列组合,比如'ABCDE',一共能排列出10钟情况,并把它们推入queue(待判断成员队列)
combin = self.Combinations(demo_ele, times)
for i in range(len(combin)):
queue.append(combin[i])
times += 1
###-----####至此已经把备选频繁寻列推入 queue ####-----###
queue = self.Make_time_queue(top, freq1, queue, queue_new)
###-----#### 至此已经把 queue 放满了备选成员 ####-----###
top = len(queue_new)# 更新队尾指针 top 的位置
###-----#### 检测 queue 中的备选序列是否频繁 ####-----###
for i in range(len(queue)):
freq_item = self.isFreq(queue[i], data) #---->> isFreq
if freq_item != 0: #如果这个成员是频繁的
queue_new.append(freq_item)
queue = []
#将列表中的字母合并成字符串
def List_to_String(self, list):
demo_string = ''
for i in range(len(list)):
demo_string = demo_string + list[i]
return demo_string
#demo_ele是待排列的字符串, times是将它们排列成几个元素
def Combinations(self, item, times):
demo_list = []
combin = []
element = ''
for i in range(1, len(item) +1):
iter = itertools.combinations(item, i)
demo_list.append(list(iter))
demo_combin = demo_list[times -1]
for i in range(len(demo_combin)):
for j in range(len(demo_combin[0])):
element += demo_combin[i][j]
combin.append(element)
element = ''
return combin
#判断item是不是频繁的
def isFreq(self, item, data):
num = 0
if '->' not in item: #类似如'ABF'
for i in range(len(data)):
for j in range(len(data[i])):
if self.isIn_Item(item, data, i, j) != 0:
num += 1
if num >= 2:
return item
else:
return 0
else: #类似如‘D->B->A’
item0 = item.split('->')
for i in range(len(data)):
array = 0
j = 0
while True:
if array == len(item0) or j == len(data[i]):
break
if len(item0[array]) >= 2: #如果类似 'BA' 形式
if self.isIn_Item(item0[array], data, i, j) == 1:
array += 1
j += 1
else:
j += 1
else:
if item0[array] in data[i][j]:
array += 1
j += 1
else:
j += 1
if array == len(item0):
num += 1
if num >= 2:
return item
else:
return 0
#判断 item 是否在 data[i][j]中
def isIn_Item(self, item, data, i, j):
demo_num = 0
for k in range(len(item)):
if item[k] in data[i][j]:
demo_num += 1
if demo_num == len(item):
return 1
else:
return 0
#
def isIn_Time(self, item0, data, i, j):
num = 0
item0_lenth = len(item0)
if item0_lenth == 2:
for m in range(j+1, len(data[i])):
if item0[1] in data[i][m]:
num += 1
else:
if item0[item0_lenth -2] in data[i][j]:
for m in range(j+1, len(data[i])):
if item0[item0_lenth -1] in data[i][m]:
num += 1
break
return num
#创造新的备选时间序列
def Make_time_queue(self, top, freq1, queue, queue_new):
for i in range(top, len(queue_new)):
# for j in range(len(freq1)):
if '->' not in queue_new[i]:
difference = self.Difference(queue_new[i], freq1)
for j in range(len(difference)):
queue.append(difference[j] + '->' +queue_new[i]) #诸如 'D->AB'
queue.append(queue_new[i] + '->' +difference[j]) #诸如 'AB->D'
else:
difference = self.Difference(queue_new[i], freq1)
for j in range(len(difference)):
queue.append(queue_new[i] + '->' + difference[j]) #诸如'B->A' 扩展成 'B->A->D'
return queue
#寻找两个字符串中的不同字母,并提取出来
def Difference(self, item, freq1):
demo_list = []
if '->' not in item:
for i in range(len(freq1)):
if freq1[i] not in item:
demo_list.append(freq1[i])
else:
demo_item = item.split('->') #将诸如'A->B'拆分成 'A','B'
demo_item_string = self.List_to_String(demo_item) #合并成'AB'
for i in range(len(freq1)):
if freq1[i] not in demo_item_string:
demo_list.append(freq1[i])
return demo_list
#----------------------------------------------------------#
# main #
#----------------------------------------------------------#
data = {0:['CD','ABC','ABF','ACDF'],
1:['ABF','E'],
2:['ABF'],
3:['DGH','BF','AGH']}
starttime = datetime.datetime.now()
s = GSP()
freq1 = s.freq1(data, 2)
s.freq_more(data, freq1)
endtime = datetime.datetime.now()
print(endtime - starttime)