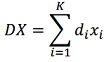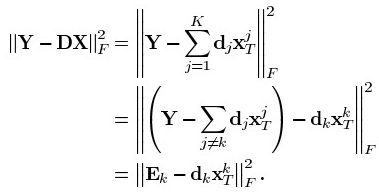K-SVD Algorithm

1. 算法简介

K-SVD可以看做K-means的一种泛化形式，K-means算法总每个信号量只能用一个原子来近似表示，而K-SVD中每个信号是用多个原子的线性组合来表示的。

K-SVD通过构建字典来对数据进行稀疏表示，经常用于图像压缩、编码、分类等应用。

2. 主要问题

Y = DX

Where Y∈R(n*N), D∈R(n*K), X∈R(k*N), X is a sparse matrix.

N is number of samples;

n is  dimension of feature /dimension of every word in dictionary;

K is the length of a coefficient/the number of atoms in the trained dictionary..

Y为要表示的信号，D为超完备矩阵（列数大于行数）， X为系数矩阵，X与Y按列对应，表示D中元素按照Xi为系数线性组合为Y，

            我们的目的是找到让X尽量稀疏的D

上面的式子本质上是相通的，只是表述形式不一样罢了。

寻找最优解(X最稀疏)是NP-Hard问题。

用追逐算法(Pursuit Algorithm)得到的次优解代替。

MatchingPursuit (MP)

OrthogonalMatching Pursuit (OMP)

BasisPursuit (BP)

FocalUnderdetermined System Solver (FOCUSS)

3. 算法求解     

       给定训练数据后一次找到全局最优的字典为NP问题，只能逐步逼近最优解.构造D算法分两步：稀疏表示和字典更新
 稀疏表示
        首先设定一个初始化的字典，用该字典对给定数据迚行稀疏表示（即用尽量少的系数尽可能近似地表示数据），得到系数矩阵X。此时，应把DX看成D中每列不X中对应每行乘积的和，也就是把DX分“片”，即：

（di 表示D的列 ， xi表示X的行），然后逐片优化。

字典更新
        初始字典往往不是最优的，满足稀疏性的系数矩阵表示的数据和原数据会有较大误差，我们需要在满足稀疏度的条件下逐行逐列更新优化，减小整体误差，逼近可用字典。剥离字典中第k（1-K）项dk的贡献，计算当前表示误差矩阵：

误差值为 ：

上式可以看做把第k个基分量剥离后，表达中产生空洞，如何找到一个新基，以更好的填补这个洞，就是SVD 方法的功能所在，当误差值稳定的时候字典基本收敛。

求解流程

      K-SVD的求解是一个迭代过程。首先，假设字典D是固定的，用MP、OMP、BP等算法，可以得到字典D上，Y的稀疏表示的系数系矩阵X，然后让X固定，根据X更新字典D,如此循环直到收敛为止。

      字典D的更新是逐列进行的。首先假设系数矩阵X和字典D都是固定的，将要更新的是字典的第k列dk ，系数矩阵X中dk对应第k行为，则

                                                                                          

得到当前误差矩阵Ek后，我们只需要调整dk和xk,使其乘积与Ek的误差尽可能的小。

对于上面的问题，如果直接用Ek的SVD分解结果来更新dk和xk，则会导致xk不稀疏，出现"发散"。换句话说，与更新d_k前的非零元所处位置和value不一样。怎么办呢？我们可以只保留系数中的非零值，再进行SVD分解就不会出现这种现象了。所以对E_k和做变换，中只保留x中非零位置的，E_k只保留d_k和中非零位置乘积后的那些项。形成，将做SVD分解，更新d_k。

具体如下：

    算法流程

     

关于SVD分解可以参考:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html                                                                       

参考：

1）K-SVD: An algorithm fordesigning overcomplete dictionaries for sparse representation (IEEE Trans. OnSignal Processing 2006)

2）http://home.ustc.edu.cn/~zywvvd/files/K-SVD.pdf

3）http://blog.csdn.net/cc198877/article/details/9167989