【jzoj100000】【ZJOI2017】【仙人掌】【树型动态规划】

题目大意

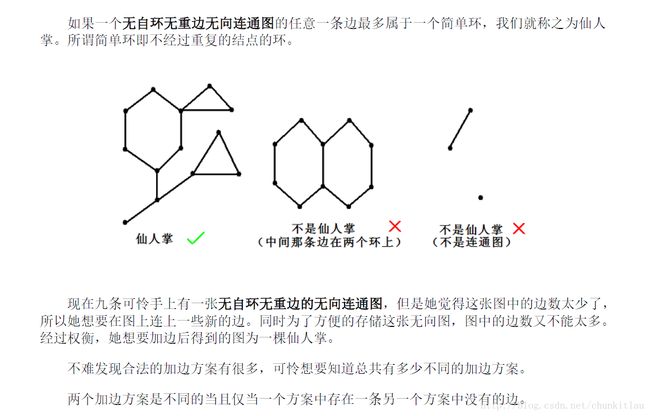
解题思路

一个比较不显然的结论，连边不可以跨过一个强连通分量，所以我们可以按强连通分量把原图变成森林，注意强连通分量的点还是可达的，只不过不能转移到同一个强连通分量的点。

考虑树的情况，我们要用一些树链覆盖原树，但是可以不覆盖。由于没有重边，所以不连边也可以视为连了重边，这样就变成了每一条边都要被覆盖。

设f[i]表示考虑到i及其子树，没有连向外部的边的方案数，g[i]表示考虑到i及其子树，有一条连向外部的边的方案数。f要考虑将儿子节点有连向外部的边的情况两两配对，设i个节点配对并留出一个空余节点的方案数，这样我们就可以将它和根节点配对。对于g的情况，首先f的情况一定适用，因为可以把连向根的点往子树外连，其次可以选一个儿子往外连，其他配对。考虑i个点配对的方案h[i]，当前节点可以不和别人配对，和根配对。也可以和前面的任意一个配对。做一次dp即可。

code

#include
#include
#include
#include
#define LF double
#define LL long long
#define ULL unsigned long long
#define fo(i,j,k) for(int i=j;i<=k;i++)
#define fd(i,j,k) for(int i=j;i>=k;i--)
#define fr(i,j) for(int i=begin[j];i;i=next[i])
using namespace std;
int const mn=5*1e5+9,mm=2*1e6,mo=998244353;LL inf=1e9;
int t,n,m,gra,tim,ok,st[mn],inst[mn],bel[mn],dfn[mn],low[mn],vis[mn],
    begin[mn],to[mm],next[mm];
LL f[mn],g[mn],h[mn];
void insert(int u,int v){
    to[++gra]=v;
    next[gra]=begin[u];
    begin[u]=gra;
}
void tarjan(int now,int pre){
    dfn[now]=low[now]=++tim;
    inst[st[++st[0]]=now]=1;
    int tmp=0;
    fr(i,now)if(to[i]!=pre){
        if(!dfn[to[i]]){
            tarjan(to[i],now);
            if(dfn[now]>low[to[i]])tmp++;
            low[now]=min(low[now],low[to[i]]);
        }else if(inst[to[i]]){
            if(dfn[now]>dfn[to[i]])tmp++;
            low[now]=min(low[now],dfn[to[i]]);
        }
    }
    if(tmp>1)ok=0;
    if(dfn[now]==low[now]){
        while(st[st[0]]!=now)
            bel[st[st[0]]]=now,inst[st[st[0]--]]=0;
        bel[st[st[0]]]=now,inst[st[st[0]--]]=0;
    }
}
void dfs(int now,int pre){
    vis[now]=1;
    LL tmp=1,tm2=0;
    fr(i,now)if((bel[to[i]]!=bel[now])&&(to[i]!=pre)){
        dfs(to[i],now);
        tmp=tmp*g[to[i]]%mo;
        tm2++;
    }
    f[now]=tmp*h[tm2]%mo;
    g[now]=(f[now]+tmp*h[tm2-1]%mo*tm2)%mo;
}
int main(){
    //freopen("cactus.in","r",stdin);
    //freopen("cactus.out","w",stdout);
    freopen("d.in","r",stdin);
    freopen("d.out","w",stdout);
    scanf("%d",&t);
    fo(cas,1,t){
        scanf("%d%d",&n,&m);
        int u,v;gra=tim=0;ok=1;
        fo(i,1,n)begin[i]=dfn[i]=vis[i]=0;
        fo(i,1,m){
            scanf("%d%d",&u,&v);
            insert(u,v);insert(v,u);
        }
        tarjan(1,0);
        if(!ok){printf("0\n");continue;}
        h[0]=h[1]=1;
        fo(i,2,n)h[i]=(h[i-1]+h[i-2]*(i-1))%mo;
        LL ans=1;
        fo(i,1,n)if(!vis[i]){
            dfs(i,0);
            ans=ans*f[i]%mo;
        }
        printf("%lld\n",ans);
    }
    return 0;
}