八皇后算法解析
今天研究力扣的一道题死活写不出来对应的算法,没办法自己算法基础太差。于是看了下答案,发现使用什么回溯算法,菜鸟表示平时开发期间写的最复杂的程序就是写了两层for循环,已经很牛逼了有木有?这个回溯算法什么鬼?于是乎百度了下,算是了解了回溯算法是什么玩意儿。这里分析一波八皇后算法来加深一下理解。
八皇后算法描述如下:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法!

下面来分析一波,假设此时我们想要在黑色方块位置放置一个皇后:
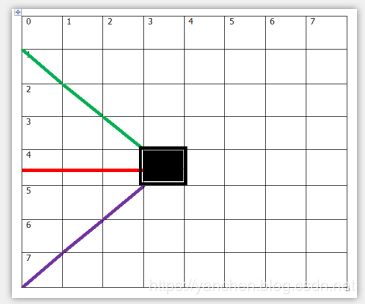
如果一列一列的放置皇后的话,图中黑色位置能放置一个皇后的合法性条件为:
1、绿色线条经过的方格没有皇后 (不处于同一斜线)
2、红色线条经过的方格没有皇后 (不处于同一行)
3、紫色线条经过的方格没有皇后 (不处于同一斜线)
也就是说如果以黑色方块位置为参照原点:(0,0)坐标点,紫色和绿色两个线条分别是斜率为1和-1的两个函数,如下图:
紫色线所代表的函数是:y = -x;
绿色先所代表的函数是:y=x;
(横坐标是列,纵坐标为行,注意行从上到下递增)
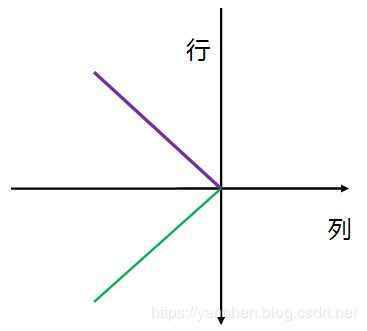
凡是位于这两条函数线上的位置(点)以及横坐标(说明位于同一行)都不能有皇后。
所以假设某一列皇后的位置用行来记录,比如queen[column] = row,意思是第column列的皇后的位置在第row行。
同行的逻辑很好判断,那么我们想要在黑色方块位置放置一个皇后,怎么判断前面几列是否在绿色线条和紫色线条上已经有了皇后呢?思路也很简单:
假设黑色方块的位置为n列,nRow行,假设位于m列的所在的行是否有皇后位于紫色线或者绿色上,那么就符合下面条件:
//假设此时即将在n列放置一个皇后,n>m
]//获取m列上皇后所在的行
int mRow = queen[m]
int nRow = queen[n];
//行的差值
int rowDiff = nRow - mRow;
//列的差值
int columnDiff = n-m;
上面代码中 rowDiff的绝对值等于columnDiff的绝对值的话,说明点位于y=x或者y=-x的函数线上:

就说明此时黑色方块的位置是不能放置皇后的,因为在紫色或者绿色线上已经有了皇后。
那么用代码来(currentColumn,curreentRow)是否可以放置皇后的方法如下
/**
* 判断当(currentRow,currentColumn)是否可以放置皇后
* @param currentColumn
* @return
*/
public boolean isLegal(int currentRow,int currentColumn) {
//遍历前面几列
for(int preColumn=0;preColumn因为博主是按照一列一列的方式来进行放置的,所以整体思路就是:在当前列逐步尝试每一行是否可以放置皇后,如果有一个可以放置皇后,就继续查看下一列的每一行是否可以放置皇后。所以代码如下:
int queen[] = new int[8];
int count = 0;
private void eightQueen(int currentColumn) {
//这个for循环的目的是尝试讲皇后放在当前列的每一行
for(int row=0;row<8;row++) {
//判断当前列的row行是否能放置皇后
if(isLegal(row,currentColumn)) {
//放置皇后
queen[currentColumn] = row;
if(currentColumn!=7) {
//摆放下一列的皇后
eightQueen(currentColumn+1);
}else {
//递归结束,此时row要++了
count++;
}
}
}//end for
}
需要注意的是当currentColumn==7的时候,说明此时已经完成了一种摆放方法,然后for循环继续执行,去尝试其他摆放方法。
测试一波,一共有92种摆放方法:
public static void main(String args[]) {
Queen queen = new Queen();
queen.eightQueen(0);
System.out.println("总共有 " +queen.count+ " 摆放方法");
}
所以结合八皇后的实现来看看到底什么是回溯算法,看百度百科解释:回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法
比如八皇后算法来说,我们根据约束条件判断某一列的某一行是否可以放置皇后,如果不可以就继续判断当前列的下一行是否可以放置皇后.如果可以放置皇后,就继续探寻下一列中可以放置皇后的那个位置。完成一次摆放后。再重新挨个尝试下一个可能的摆放方法。
下面用一个力扣的题再次巩固下回溯算法的应用。该题描述如下:
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明:所有数字(包括 target)都是正整数。解集不能包含重复的组合。
示例 1:输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
做该题的重要条件是无重复的数组,那么问题就很好解了。
首先对数组从大到小排序。这是解题的关键。
然后为了减少不必要的遍历,我们要对原来的数组进行截取:
List> res = new ArrayList<>();
//重要的要大小排列
Arrays.sort(candidates);
//说明原数组中就没有满足target的数
if (candidates[0] > target) {
return res;
}
List newCandidates= new ArrayList();
int len = candidates.length;
// 取小于target的数 组成一个临时数组
for (int i = 0; i < len; i++) {
int num = candidates[i];
if (num > target) {
break;
}
newCandidates.add(num);
} // end for
通过上面的步骤我们拿到了一个从小到大排列的无重复数组newCandidates,数组中的元素都<=target.
因为数组从小到大排列,所以我们有如下几种情况,以candidates = [2,3,5], target = 8为例:
符合条件的子数组满足条件如下
1、target循环减去一个数,如果能一直减到到差值等于0,那么这个数组成的数组就是一个解,比如[2,2,2,2];
2、target减去一个数,然后形成了一个新的newTarget=target-num[i],让这个newTarget减去下一个数num[i+1],然后执行步骤1,则又是一个解,比如[2,3,3];(其实步骤1是步骤2的一个特例)
3、target减去一个数,然后形成了一个新的newTarget=target-num[i],让这个newTarget减去下一个数num[i+1],如果能一直减到到差值等于0说明又是一个解.,比如[3,5];
如此得到了一个规律,只要是相减之后得到差值=0,就说明就得到一个解。
得到一个新的解之后继续循环数组中的下一个数字,继续执行1,2,3步骤即可。
所以完成的解法如下:
class Solution {
public List> combinationSum(int[] candidates, int target) {
List> res = new ArrayList<>();
//重要的要大小排列
Arrays.sort(candidates);
List temp = new ArrayList();
if (candidates[0] > target) {
return res;
}
int len = candidates.length;
// 取小于target的数 足证一个临时数组
for (int i = 0; i < len; i++) {
int num = candidates[i];
if (num > target) {
break;
}
temp.add(num);
} // end for
//
find(res, new ArrayList<>(), temp, target, 0);
return res;
}
public void find(List> res, List tmp, List candidates, int target, int start){
//target==0.找到一个新的解
if (target == 0) {
res.add(new ArrayList<>(tmp));
}else if(target>0){
for (int i = start; i < candidates.size(); i++) {
int num = candidates.get(i);
if(num<=target){
tmp.add(num);
//查找新的target
int newTarget = target-num;
find(res, tmp, candidates, newTarget, i);
tmp.remove(tmp.size() - 1);
}
}//end for
}
}
}