最大熵模型-最大熵原理与最大熵模型定义
基本概率
熵
熵是表示随机变量的不确定性的度量。熵越大,随机变量的不确定性越大。假设离散变量 X X 的概率分布式 P(X) P ( X ) ,熵的定义为:
H(p)=−∑i=1Npilogpi H ( p ) = − ∑ i = 1 N p i l o g p i
因
∑i=1Npi=1 ∑ i = 1 N p i = 1
根据Jensen不等式,有:
H(p)=−∑i=1Npilogpi≤log(∑i=1N(pi×1pi))=logN H ( p ) = − ∑ i = 1 N p i l o g p i ≤ l o g ( ∑ i = 1 N ( p i × 1 p i ) ) = l o g N
因此熵满足下列不等式:
0≤H(p)≤logN 0 ≤ H ( p ) ≤ l o g N
当且仅当X符合均匀分布时右边不等号成立。
联合熵
根据熵的定义,两个随机变量的 X X , Y Y 的联合熵为:
H(X,Y)=−∑x∈X,y∈Yp(x,y)logp(x,y) H ( X , Y ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g p ( x , y )
条件熵
条件熵表示给定随机变量 X X 时, Y Y 的熵( (X,Y) ( X , Y ) 同时发生时包含的熵减去 X X 单独发生时的熵):
H(Y|X)=H(X,Y)−H(X)=−∑x∈X,y∈Yp(x,y)logp(x,y)−∑x∈Xp(x)logp(x)=−∑x∈X,y∈Yp(x,y)logp(x,y)−∑x∈(∑y∈YXp(x,y)logp(x))=−∑x∈X,y∈Yp(x,y)logp(x,y)−∑x∈X,y∈Yp(x,y)logp(x)=−∑x∈X,y∈Yp(x,y)(logp(x,y)−log(p(x))=−∑x∈X,y∈Yp(x,y)logp(y|x)=−∑x∈X,y∈Yp(x)p(y|x)logp(y|x) H ( Y | X ) = H ( X , Y ) − H ( X ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g p ( x , y ) − ∑ x ∈ X p ( x ) l o g p ( x ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g p ( x , y ) − ∑ x ∈ ( ∑ y ∈ Y X p ( x , y ) l o g p ( x ) ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g p ( x , y ) − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g p ( x ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) ( l o g p ( x , y ) − l o g ( p ( x ) ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) l o g p ( y | x ) = − ∑ x ∈ X , y ∈ Y p ( x ) p ( y | x ) l o g p ( y | x )
$$
最大熵原理
最大熵原理是概率模型学习中一个准则,其核心思想为:在学习概率模型时,所有可能的模型中熵最大的模型是最好的模型。通常用约束条件确定概率模型的集合。所以最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
最大熵原理的直观解释
假设预测一个骰子的点数,满足约束条件:
∑i=16P(X=i)=1 ∑ i = 1 6 P ( X = i ) = 1
满足这个约束条件的分布有无数多个,没有任何先验知识的情况下,假设分布式均匀的,即
P(X=i)=16i=1,2,3,4,5,6 P ( X = i ) = 1 6 i = 1 , 2 , 3 , 4 , 5 , 6
如果从一些先验知识中得到一些概率值得约束条件,例如:
P(X=1)+P(X=2)=14 P ( X = 1 ) + P ( X = 2 ) = 1 4
∑i=16P(X=i)=1 ∑ i = 1 6 P ( X = i ) = 1
缺少信息的情况下认为
X=1 X = 1 和
X=2 X = 2 是等概率的,则:
P(X)={18316X=1,2X=3,4,5,6 P ( X ) = { 1 8 X = 1 , 2 3 16 X = 3 , 4 , 5 , 6
simplex与概率模型
如果用欧式空间中的simplex来表示随机变量 X X ,则 simplex中三个顶点分别代表随机变量 X X 的三个取值A,B,C。这里定义simplex中任意一点 p p 到三条边的距离之和(恒等于三角形的高)为1,点到其所对的边为该取值的概率,比如任给一点p,则 P(A) P ( A ) 等于p到边BC的距离,如果给定如下概率:
P(A)=1,P(B)=P(C)=0 P ( A ) = 1 , P ( B ) = P ( C ) = 0
P(A)=P(B)=P(C)=13 P ( A ) = P ( B ) = P ( C ) = 1 3
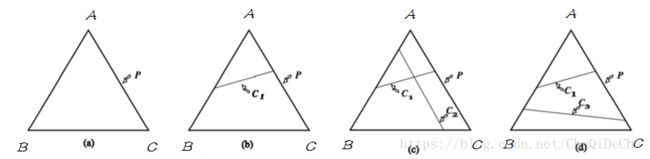
分别表示下图两种情况:

将simplex与概率模型联系起来:
1. 图(a)表示没有任何约束情况下,simplex中的任意一点表示一个概率分布,只需要找到满足最大熵条件的点即可。
2. 图(b)表示有一个约束条件,模型集合被限制在直线
C1 C 1 熵,则应该满足
C1 C 1 约束下找到熵最大的模型。
3. 图(c)表示有两个约束条件,模型此时被限制在一个点上,具有唯一解。
4. 图(d)表示两个约束没有交集,此时没有解。但约束通常从数据集中取得,所以不会出现不一致情况。
最大熵模型的定义
将最大熵原理应用到分类问题即得到最大熵模型。
给定一个训练数据集:
T={(x1,y1),(x2,y2),⋅⋅⋅,(xN,yN)} T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋅ ⋅ ⋅ , ( x N , y N ) }
其中
x∈X⊆Rn x ∈ X ⊆ R n 表示输入,
y∈Y⊆R y ∈ Y ⊆ R 表示输出,N为样本数。最大熵模型的学习目标是
用最大熵原理选择最好的分类模型,即,对于给定的输入
X X ,以条件概率
P(Y|X) P ( Y | X ) 输出
Y Y 。
联合分布和边缘分布的经验分布
给定训练数据集是,可以确定联合分布 P(X,Y) P ( X , Y ) 和边缘分布 P(X) P ( X ) 的经验分布:
P˜(X=x,Y=y)=ν(X=x,Y=x)N P ~ ( X = x , Y = y ) = ν ( X = x , Y = x ) N
P˜(X=x)=ν(X=x)N P ~ ( X = x ) = ν ( X = x ) N
其中
ν(X) ν ( X ) 表示训练数据集中满足条件
X X 的频数。
特征函数
从训练数据集 T T 中抽取若干特征,对于一个给定的样本 (x,y) ( x , y ) ,特征函数可以定义为任意实值函数。考虑最简单的二值函数:
f(x,y)={1,0,若x,y满足某一事实否则 f ( x , y ) = { 1 , 若 x , y 满 足 某 一 事 实 0 , 否 则
假设判断我们判断一个人是否喜欢玩游戏,一直训练集:
| 编号 |
年龄 |
是否喜欢玩游戏 |
| 1 |
未成年 |
是 |
| 2 |
未成年 |
是 |
| 3 |
成年 |
否 |
| 4 |
未成年 |
否 |
通过观察数据集,可以发现:若一个人未成年,则喜欢玩游戏,可用特征函数表示为:
f(x,y)={1,0,未成年否则 f ( x , y ) = { 1 , 未 成 年 0 , 否 则
定义这个特征函数之后,对于训练数据集有:
| 编号 |
f(x,y) f ( x , y ) |
| 1 |
1 |
| 2 |
1 |
| 3 |
0 |
| 4 |
0 |
对于同一个数据集,特征值函数可以有多个
约束条件
对于任意一个特征值函数 f(x,y) f ( x , y ) 关于经验分布 P˜(X,Y) P ~ ( X , Y ) 的期望:
E˜p˜(f)=∑x,yp˜(x,y)f(x,y) E ~ p ~ ( f ) = ∑ x , y p ~ ( x , y ) f ( x , y )
对于任意一个特征值函数
f(x,y) f ( x , y ) 在给定模型上关于
P˜(X,Y) P ~ ( X , Y ) 的期望:
Ep(f)=∑x,yp(x,y)f(x,y)=∑x,yp(x)p(y|x)f(x,y)=∑x,yp˜(x)p(y|x)f(x,y) E p ( f ) = ∑ x , y p ( x , y ) f ( x , y ) = ∑ x , y p ( x ) p ( y | x ) f ( x , y ) = ∑ x , y p ~ ( x ) p ( y | x ) f ( x , y )
由于
p(x) p ( x ) 未知,用
p˜(x) p ~ ( x ) 来近似。
如果模型能够获取训练数据中的信息,那么就可以假设两个期望值相等,即:
E˜p˜(f)=Ep(f) E ~ p ~ ( f ) = E p ( f )
或:
∑x,yp˜(x,y)f(x,y)=∑x,yp˜(x)p(y|x)f(x,y) ∑ x , y p ~ ( x , y ) f ( x , y ) = ∑ x , y p ~ ( x ) p ( y | x ) f ( x , y )
对于n个特征值函数,则有n个约束条件。
最大熵模型
假设满足所有约束条件的集合为:
C≡{P|E˜p˜(fi)=Ep(fi)} C ≡ { P | E ~ p ~ ( f i ) = E p ( f i ) }
条件概率$P(Y|X)的条件熵的定义为:
H(P)=−∑x,yp˜(x)p(y|x)logp(y|x) H ( P ) = − ∑ x , y p ~ ( x ) p ( y | x ) l o g p ( y | x )
模型 C C 中熵最大的模型称为最大熵模型。
参考文献
- 李航《统计学习》
- 最大熵学习笔记(三)最大熵模型
- 最大熵模型 Maximum Entropy Model

