KMP算法总结

版权声明：本文为博主原创文章，未经博主允许不得转载。

目录(?)[-]

1. KMP算法
   1.       一BF算法简介
   2. 二KMP算法
      1. 1next数组
      2. KMP匹配过程
      3. 时间复杂度分析

搞ACM也有三年了，期间学习了不少算法，到12月把上海站打完也要成退役狗了。最近突然想把学过的一些算法回过头来好好总结一下，于是就有了我的算法总结系列。这是这个系列的开端，所以先写一个简单点的算法，以后会慢慢复习一些复杂的算法，最后还是希望自己能够坚持下去吧。

KMP算法

KMP算法是一种线性时间复杂度的字符串匹配算法，它是对BF（Brute-Force,最基本的字符串匹配算法）的改进。对于给定的原始串S和模式串T，需要从字符串S中找到字符串T出现的位置的索引。KMP算法由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现，因此人们称它为Knuth--Morris--Pratt算法，简称KMP算法。在讲解KMP算法之前，有必要对它的前身--BF算法有所了解，因此首先将介绍最朴素的BF算法。

      一：BF算法简介

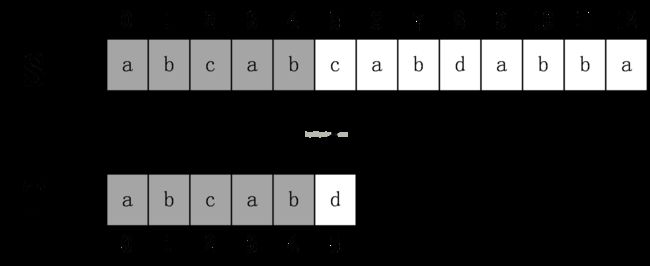
如上图所示，原始串S=abcabcabdabba,模式串为abcabd。（下标从0开始）从s[0]开始依次比较S[i] 和T[i]是否相等，直到T[5]时发现不相等,这时候说明发生了失配，在BF算法中，发生失配时，T必须回溯到最开始，S下标+1，然后继续匹配，如下图所示：

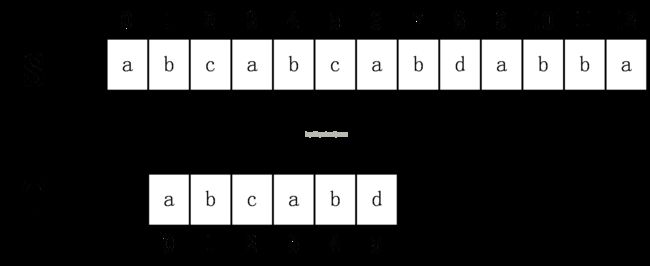
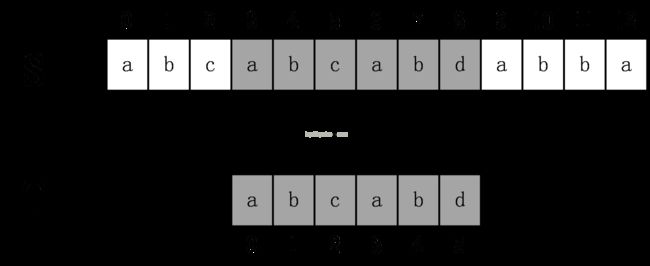
这次立即发生了失配，所以继续回溯，直到S开始下表增加到3，匹配成功。

容易得到，BF算法的时间复杂度是O(n*m)的，其中n为原始串的长度，m为模式串的长度。BF的代码实现也非常简单直观，这里不给出，因为下一个介绍的KMP算法是BF算法的改进，其时间复杂度为线性O(n+m)，算法实现也不比BF算法难多少。

二：KMP算法

前面提到了朴素匹配算法，它的优点就是简单明了，缺点当然就是时间消耗很大，既然知道了BF算法的不足，那么就要对症下药，设计一种时间消耗小的字符串匹配算法。

KMP算法就是其中一个经典的例子，它的主要思想就是：

在匹配匹配过程中发生失配时，并不简单的从原始串下一个字符开始重新匹配，而是根据一些匹配过程中得到的信息跳过不必要的匹配，从而达到一个较高的匹配效率。

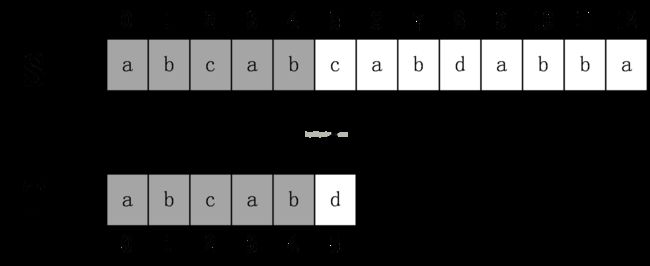
还是前面的例子，原始串S=abcabcabdabba,模式串为abcabd。当第一次匹配到T[5]!=S[5]时，KMP算法并不将T的下表回溯到0，而是回溯到2，S下标继续从S[5]开始匹配，直到匹配完成。

那么为什么KMP算法会知道将T的下标回溯到2呢？前面提到，KMP算法在匹配过程中将维护一些信息来帮助跳过不必要的检测，这个信息就是KMP算法的重点 --next数组。（也叫fail数组，前缀数组）。

1：next数组

（1）next数组的定义：

设模式串T[0,m-1]，（长度为m）,那么next[i]表示既是是串T[0,i-1]的后缀又是串T[0,i-1]的前缀的串最长长度(不妨叫做前后缀)，注意这里的前缀和后缀不包括串T[0,i-1]本身。

如上面的例子，T=abcabd,那么next[5]表示既是abcab的前缀又是abcab的后缀的串的最长长度，显然应该是2，即串ab。注意到前面的例子中，当发生失配时T回溯到下表2，和next[5]数组是一致的，这当然不是个巧合，事实上，KMP算法就是通过next数组来计算发生失配时模式串应该回溯到的位置。

2.next数组的求解思路

　　通过上文完全可以对kmp算法的原理有个清晰的了解，那么下一步就是编程实现了，其中最重要的就是如何根据待匹配的模版字符串求出对应每一位的最大相同前后缀的长度。我先给出我的代码：

 1 void makeNext(const char P[],int next[])
 2 {
 3     int q,k;//q:模版字符串下标；k:最大前后缀长度
 4     int m = strlen(P);//模版字符串长度
 5     next[0] = 0;//模版字符串的第一个字符的最大前后缀长度为0
 6     for (q = 1,k = 0; q < m; ++q)//for循环，从第二个字符开始，依次计算每一个字符对应的next值
 7     {
 8         while(k > 0 && P[q] != P[k])//递归的求出P[0]···P[q]的最大的相同的前后缀长度k
 9             k = next[k-1];          //不理解没关系看下面的分析，这个while循环是整段代码的精髓所在，确实不好理解  
10         if (P[q] == P[k])//如果相等，那么最大相同前后缀长度加1
11         {
12             k++;
13         }
14         next[q] = k;
15     }
16 } 

 　　现在我着重讲解一下while循环所做的工作：

1. 　　已知前一步计算时最大相同的前后缀长度为k（k>0），即P[0]···P[k-1]；
2. 　　此时比较第k项P[k]与P[q],如图1所示
3. 　　如果P[K]等于P[q]，那么很简单跳出while循环;
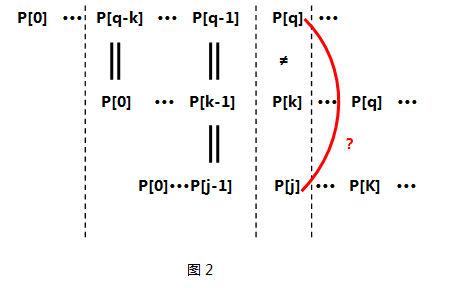
4. 　　关键！关键有木有！关键如果不等呢？？？那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀，可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢？？？是啊！为什么呢？ 原因在于P[k]已经和P[q]失配了，而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同，看来P[0]···P[k-1]这么长的子串是用不了了，那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1])，看看它的下一项P[j]是否能和P[q]匹配。如图2所示

 

 

注意：在回溯过程中可能有一种情况,就是找不到合适的po满足上述4个条件，这说明T[0,i]的最长前后缀串长度为0，直接将next[i+1]赋值为0,即可。

 //计算串str的next数组
 int GETNEXT(char *str,int next)
 {
     int len=strlen(str);
     next[0]=next[1]=0;//初始化
     for(int i=1;i
     {
         int j=next[i];
         while(j&&str[i]!=str[j])//一直回溯j直到str[i]==str[j]或j减小到0
         j=next[j];
         next[i+1]=str[i]==str[j]?j+1:0;//更新next[i+1]
     }
     return len;//返回str的长度
 }

以上是计算next数组的代码实现。是不是非常简短呢。

2.KMP匹配过程

有了next数组，我们就可以通过next数组跳过不必要的检测，加快字符串匹配的速度了。那么为什么通过next数组可以保证匹配不会漏掉可匹配的位置呢？

首先，假设发生失配时T的下标在i，那么表示T[0,i-1]与原始串S[l,r]匹配,设next[i]=j，根据KMP算法，可以知道要将T回溯到下标j再继续进行匹配，根据next[i]的定义，可以得到T[0,j-1]和S[r-j+1,r]匹配，同时可知对于任何j

同next数组的计算，在一般情况下，可能回溯到next[i]后再次发生失配，这时只要继续回溯到next[j]，如果不行再继续回溯，最后回溯到next[0]，如果还不匹配，这时说明原始串的当前位置和T的开始位置不同，只要将原始串的当前位置+1，继续匹配即可。

下面给出KMP算法匹配过程的代码:

 //返回S串中第一次出现模式串T的开始位置
 int KMP(char *S,char *T)
 {
     int l1=strlen(S),l2=GETNEXT(T);//l2为T的长度,getnext函数将在下面给出
     int i,j=0,ans=0;
     for(i=0;i
     {
         while(j&&S[i]!=T[j])//发生失配则回溯
         j=next[j];
         if(S[i]==T[j])
         j++;
         if(j==l2)//成功匹配则退出
         break;
     }
     if(j==l2)
     return i-l2+1;//返回第一次匹配成功的位置
     else
     return -1;//若匹配不成功则返回-1
 }

3.时间复杂度分析

前面说到，KMP算法的时间复杂度是线性的，但这从代码中并不容易得到，很多读者可能会想，如果每次匹配都要回溯很多次，是不是会使算法的时间复杂度退化到非线性呢？

其实不然，我们对代码中的几个变量进行讨论，首先是kmp函数，显然决定kmp函数时间复杂度的变量只有两个，i和j，其中i只增加了len次，是O(len)的，下面讨论j,因为由next数组的定义我们知道next[j]

到这里，KMP算法的实现已经完毕。但是这还不是最完整的的KMP算法，真正的KMP算法需要对next数组进行进一步优化，但是现在的算法已经达到了时间复杂度的下线，而且，现在的next数组的定义保留了一些非常有用的性质，这在解决一些问题时是很有帮助的。

对于优化后的KMP算法，有兴趣的朋友可以自行查阅相关资料。