Kmeans聚类①——数据标准化&归一化&正则化

Kmeans系列目录：
Kmeans聚类②——Sklearn数据生成器（make_blob/classification/circles/make_moons)
Kmeans聚类③——Kmeans聚类原理&轮廓系数&Sklearn实现
Kmeans聚类实例④——电商RFM模型聚类
Kmeans聚类实例⑤——直播行业用户质量分析

在进行机器学习之前，经常需要对训练数据进行标准化/归一化/正则化，为什么呢？
1）去除量纲的影响，将有量纲的数值变成无量纲的纯数值；
2）是去除各特征之间数值差异过大的问题，比如一个向量（uv:10000, rate:0.03,money: 20)，如果要与其它向量一起计算欧氏距离或者余弦相似度时，会向uv倾斜非常严重，导致其余2个特征对模型的贡献度非常低
3）提升训练的速度，防止过拟合

一、Z-score标准化

Z-score标准化是将数据变成均值为0，标准差为1的分布，此方法比较适合于本身较符合正太分布的数据集。有2种方法，1是基于python本身函数计算，如下：

import pandas as pd
data = pd.read_csv('chat.csv',encoding='gbk')
df = data.values
x = df[:,:4]
print(x[:3])

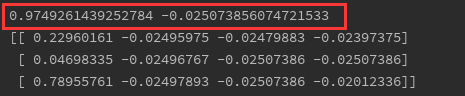
通过调用x.mean和x.std()，可以看到均值为0，标准差为1

x = (x-x.mean())/x.std()
print(x.mean(),x.std())
print(x[:3])

另1种是直接调用sklearn库

from sklearn import preprocessing
t= preprocessing.StandardScaler().fit(x)
x=t.transform(x)
print(x.mean(),x.std())
print(x[:3])

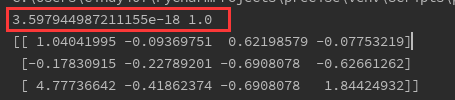
可以看出均值也是0，标准差为1。建议用后者，因为后续可以直接用模型对测试数据进行标准化，这样能保证训练集和测试集是一样的标准方法

二、最大最小归一化

有一个很形象的比喻，如果有一次期末考试题特别难，大家都在59分以下，学校觉得此成绩不太妥当，想进行整体提升，但是怎么提能保证公平性呢？

最大最小化就出场了：最终分数 = （原始分数-最小分数）/(最大分数-最小分数）*100

假设最大分数为50，最小为10，那么最终的最大分数 = （50-10）/(50-10)*100=100分
如果不乘以100，那么数值区间就在[0,1]之间，如果想区间在[-1,10]，可以将分子中的最小值改为均值

x = (x-x.min())/(x.max()-x.min())
print(x.max(),x.min())
print(x[:3])

x = (x-x.mean())/(x.max()-x.min())
print(x.max(),x.min())
print(x[:3])

调用skearn库更方便

t= preprocessing.MinMaxScaler().fit(x)
x=t.transform(x)
print(x.max(),x.min())
print(x[:3])

最大最小化的优点是能确保所有的数据都在理想的区间内，缺点就是当加入新的数据后， 可能会导致最大最小值变化，从而全部的数据都会重新计算

三、正则化

在训练数据不够多时，常常会导致过拟合，正则化主是防止过拟合的一种方法
常用的就L1和L2正则化，L1是将每一个样本的各向量绝对值之和作为范数，再用每个向量去除了这个范数，就得到这个样本L1正则化后的向量；L2是将每一个样本的向量先平方和再开方作为范数，再相除，如果用公式表达就是：

t= preprocessing.Normalizer().fit(x)
x=t.transform(x)
print(x[:3]) 

四、归一化实战

背景：我们基于观看UV、回头率、观看UV、送礼UV和送礼金额，通过一个特定的算法得到了平台每一位主播的评分，直接通过最大最小归一化再乘以*1000的方式缩放至0-1000区间。

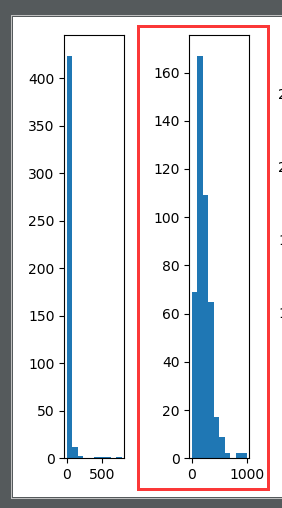
结果：发现主播评分在900以上的非常少，大部分都集中在300以下，如图：

这样的话除了评分较高的几位主播，其它的几百位主播根本拉不开差距，这样的评分不能如实反应出主播的质量差异，要优化

① 先开1/3方缩小差距再最大最小归一化

import pandas as pd
import json
import numpy as np
import matplotlib.pyplot as plt
import math

# 读取评分
with open('score.txt','r') as f:
    data = f.read()
print(data)
data = data.replace("'","\"") # json文件格式不正确，key是单引号，换成双引号
print(data)
data = json.loads(data) 

data = pd.Series(data).sort_values(ascending=False)
# 原始分数
fig = plt.figure()
ax1 = fig.add_subplot(151)
ax1.hist(data)

# 先开1/3方再最大最化归一化
data1 = pow(data,1/3)
data1 = (data1-data1.min())/(data1.max()-data1.min())*1000
ax2 = fig.add_subplot(152)
ax2.hist(data1)

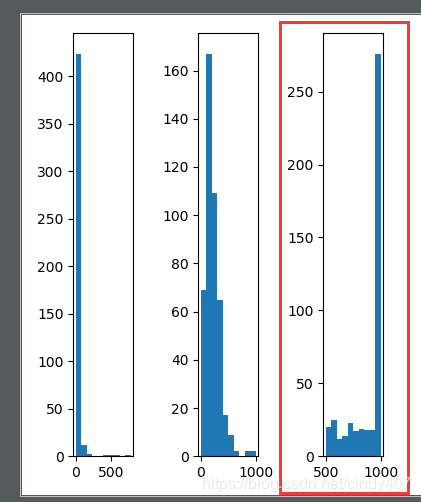
与原始评分相比，确实要分散一些，效果有提升

② logistic函数直接缩放至[0,1]，再乘以1000

#  sigmoid曲线 logistic * 1000
data2 = 1/(1+np.exp(-data)) * 1000
ax3 = fig.add_subplot(153)
ax3.hist(data2)

评分竟然由底部聚集变成了顶部聚集，也没法拉开差距了，不行

③ log10归一化* 1000，为了防止出现负数，给每个分数+1

data3 = np.log(data+1.0)/np.log(data.max()+1)*1000
ax4 = fig.add_subplot(154)
ax4.hist(data3)

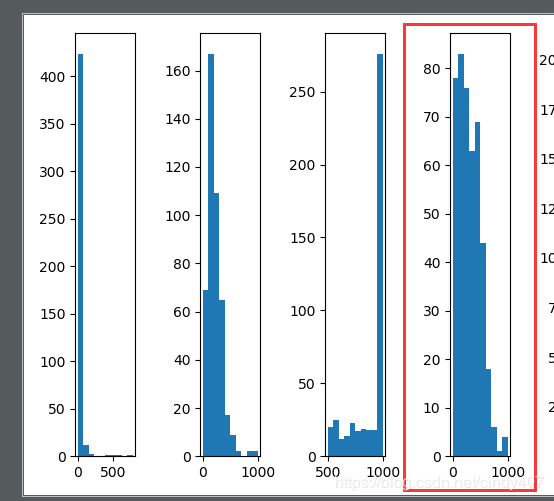
哎，这个不就是我们理想的分布嘛，已经非常满足我们的需求了，但是为了全面，我还是做了下一种尝试

④ atan函数归一化

# atan函数归一化
data = pd.DataFrame(data,columns=['score'])
data['score'] = data['score'].apply(lambda x: math.atan(float(x)+0.1)*2.0/np.pi * 1000)
ax5 = fig.add_subplot(155)
ax5.hist(data['score'])
plt.show()

这个与logistic函数非常像，都是向顶部聚集，所以最后坚定地选择了log10函数，完美！

五、 总结

选择哪种归一化方式其实取决于原始数据的分布和你想要达到的分布，而不是随机选择就可以。要尽量多多尝试，有对比才能知道哪个最适合你！