C++实现二叉搜索树（二叉排序树）模板类

参考了Weiss的数据结构与算法分析C++描述第三版

在中文版中，第99页貌似有个错误。在4.3.6 平均情况分析中，书上写的是“直观地，我们期望前一节所有的操作特别是makeEmpty 和 operator=都花费O(logN)时间，……”，我感觉不太对，因为makeEmpty 和 operator=都遍历了每个节点，花费应该是O(N)才对，其他的操作，比如查找元素，查找最大最小之类的，应该是O(logN)。然后我找了一下英文原版书，是第四版了，原文是“Intuitively, we expect that all of the operations described in this section, except makeEmpty and copying, should take O(logN)time,......”。原来是翻译错误。应该是“除了makeEmpty 和 operator=都花费O(logN)时间”。

下面记录一下今天的代码

首先是定义了二叉查找树的模板：BinarySearchTree.h

#ifndef BINARY_SEARCH_TREE_H
#define BINARY_SEARCH_TREE_H
#include
using namespace std;

template 
class BinarySearchTree
{
public:
	BinarySearchTree() :m_root(nullptr){}
	BinarySearchTree(const BinarySearchTree &rhs)
	{
		m_root = clone(rhs.m_root);
	}
	~BinarySearchTree()
	{
		makeEmpty();
	}

	/**
	* 找到树中的最小值，通过调用private的findMin实现递归
	*/
	const Comparable & findMin() const
	{
		return findMin(m_root)->element;
	}

	/**
	* 找到树中的最大值，通过调用private的findMax实现递归
	*/
	const Comparable & findMax() const
	{
		return findMax(m_root)->element;
	}

	/**
	* 当x找到时返回真，否则返回假 
	* 调用了private的那个同名函数，这个是为了递归实现
	*（因为private中包含了一个BinaryNode的指针t）
	*/
	bool contains(const Comparable &x) const
	{
		return contains(x, m_root);
	}

	/**
	* 判断树是否为空
	*/
	bool isEmpty() const
	{
		return m_root == nullptr;
	}

	/**
	* 把树遍历一遍（中序,因为中序可以保证顺序输出）
	*/
	void printTree(ostream & out= cout) const
	{
		if (isEmpty())
			out << "Empty tree!" << endl;
		else
			printTree(m_root, out);
	}

	/**
	* 清空树
	*/
	void makeEmpty()
	{
		makeEmpty(m_root);
	}

	/**
	* 把x插入树中，如果重复了就忽略
	*/
	void insert(const Comparable &x)
	{
		insert(x, m_root);
	}

	/**
	* 把x从树中删除。如果x不在树中就什么都不做。
	*/
	void remove(const Comparable &x)
	{
		remove(x, m_root);
	}

	/**
	* 深拷贝
	*/
	const BinarySearchTree & operator= (const BinarySearchTree &rhs)
	{
		if (this != &rhs)
		{
			BinaryNode *tmp = clone(rhs.m_root);
			makeEmpty();
			m_root = tmp;
		}
		return *this;
	}


private:
	struct BinaryNode{
		Comparable element;
		BinaryNode *left;
		BinaryNode *right;
		
		BinaryNode(const Comparable &theElement,
			BinaryNode *lt,
			BinaryNode *rt)
			: element(theElement), left(lt), right(rt) {}
	};

	BinaryNode *m_root;

	/**
	* 在树t中插入元素x，如果重复则什么也不做
	*/
	void insert(const Comparable &x, BinaryNode * &t) const
	{
		if (t == nullptr)
			t = new BinaryNode(x, nullptr, nullptr);
		else if (x < t->element)
			insert(x, t->left);
		else if (t->element < x)
			insert(x, t->right);
		else
			; // 表示在树中找到了x，则什么也不做
	}

	/**
	* 在树t中删除元素x
	*/
	void remove(const Comparable &x, BinaryNode * &t) const
	{
		if (t == nullptr)
			return; // 没有找要删除的节点x
		if (x < t->element)
			remove(x, t->left);
		else if (t->element < x)
			remove(x, t->right);
		else if (t->left != nullptr &&
		t->right != nullptr)
		{
			t->element = findMin(t->right)->element;
			remove(t->element, t->right);
		}
		else
		{
			BinaryNode * oldNode = t;
			t = (t->left != nullptr) ? t->left : t->right;
			delete oldNode;
		}
	}

	/**
	* 查找最小的元素, 通过递归的方法
	*/
	BinaryNode * findMin(BinaryNode *t) const
	{
		if (t == nullptr)
			return nullptr;
		if (t->left == nullptr)
			return t;
		return findMin(t->left);
	}

	/**
	* 查找最大的元素, 通过循环的方法
	*/
	BinaryNode * findMax(BinaryNode *t) const
	{
		if (t != nullptr)
			while (t->right != nullptr)
				t = t->right;
		return t;
	}

	/**
	* 通过遍历的方法查找x是否在树（或子树）t中
	*/
	bool contains(const Comparable &x, BinaryNode * t) const
	{
		if (t == nullptr) // 遍历中未找到元素的中止条件
			return false;
		else if (x < t->element)
			return contains(x, t->left);
		else if (t->element < x)
			return contains(x, t->right);
		else // 如果 x 不大于 也 不小于t所指的节点中的元素，则x==t->element
			return true;
	}

	/**
	* 清空树
	*/
	void makeEmpty(BinaryNode * &t)
	{
		if (t != nullptr)
		{
			makeEmpty(t->left);
			makeEmpty(t->right);
			delete t;
		}
		t = nullptr;
	}

	/**
	* 打印子树
	*/
	void printTree(BinaryNode *t, ostream & out) const
	{
		if (nullptr != t)
		{
			printTree(t->left, out);
			out << t->element << endl;
			printTree(t->right, out);
		}
	}

	/**
	* 复制子树
	*/
	BinaryNode * clone(BinaryNode *t) const
	{
		if (t == nullptr)
			return nullptr;

		return new BinaryNode(t->element, clone(t->left), clone(t->right));
	}

};
#endif

测试用的文档：testDemo.cpp

#include
#include
#include
using namespace std;

#include"BinarySearchTree.h"

int main()
{
	BinarySearchTree t; // 创建一个二叉搜索树

	uniform_int_distribution u(0,200); // 设置随机数分布
	default_random_engine e(time(0)); // 设置随机数引擎（通过时间作为种子）

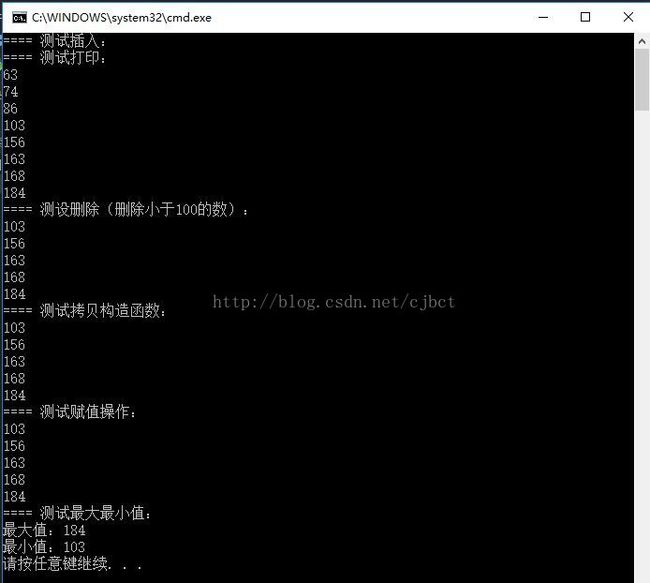
	cout << "==== 测试插入：" << endl;
	for (size_t i = 0; i < 8; ++i)
	{
		t.insert(u(e));
	}
	cout << "==== 测试打印："<< endl;
	t.printTree();
	cout << "==== 测设删除（删除小于100的数）：" << endl;
	for (size_t i = 0; i < 100; ++i)
	{
		t.remove(i);
	}
	t.printTree();
	cout << "==== 测试拷贝构造函数：" << endl;
	BinarySearchTree t2(t);
	t2.printTree();
	cout << "==== 测试赋值操作：" << endl;
	BinarySearchTree t3;
	t3 = t;
	t.printTree();
	cout << "==== 测试最大最小值：" << endl;
	cout << "最大值：" << t.findMax() << endl;
	cout << "最小值：" << t.findMin() << endl;

	return 0;
}

结果如图：