线性代数概述

 2x−y    =0   2 x − y         = 0
−x+2y−z=−1 − x + 2 y − z = − 1
−3y+4z=4 − 3 y + 4 z = 4

行理解
A= ⎡⎣⎢2−10−12−30−14⎤⎦⎥ [ 2 − 1 0 − 1 2 − 1 0 − 3 4 ] b= ⎡⎣⎢0−14⎤⎦⎥ [ 0 − 1 4 ]

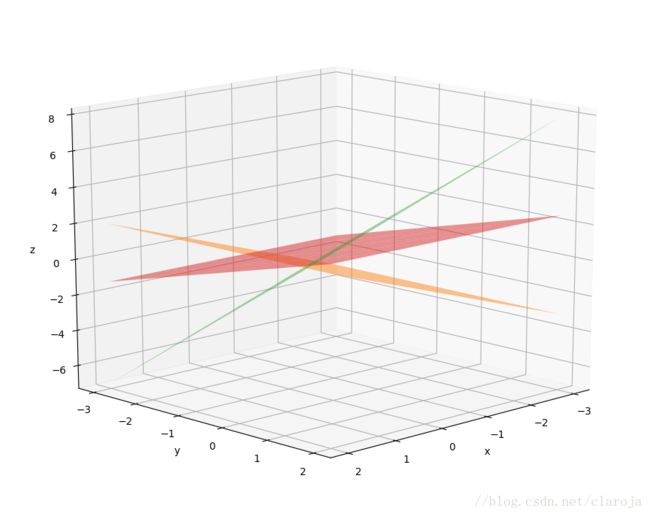
三个平面不平行就能相交于一点,做出图像,python代码如下

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-3,3)
X,Y = np.meshgrid(x,x)

z1 = np.arange(-3,3)
z1 = np.meshgrid(z1,z1)[0]    # 2x -  y + 0z =  0
z2 = lambda x,y: -x + 2*y + 1                # -x + 2y -  z = -1
z3 = lambda x,y: 0*X + (3/4)*y +1   # 0x - 3y + 4z =  4

fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x"); ax.set_ylabel("y"); ax.set_zlabel("z")

surf = ax.plot_surface(X, Y, z1, color="C1", linewidth=0, shade=False, alpha = 0.5)
surf = ax.plot_surface(X, Y, z2(X,Y), color="C2", linewidth=0, shade=False, alpha = 0.5)
surf = ax.plot_surface(X, Y, z3(X,Y), color="C3", linewidth=0, shade=False, alpha = 0.5)

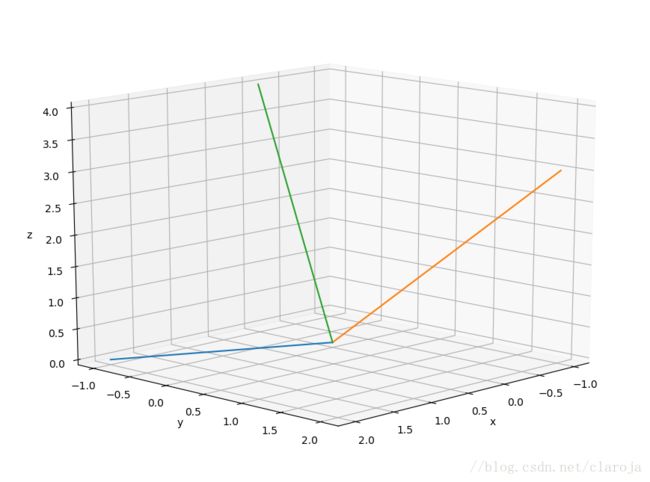
plt.show()

列理解
x ⎡⎣⎢2−10⎤⎦⎥ [ 2 − 1 0 ] +y ⎡⎣⎢−123⎤⎦⎥ [ − 1 2 3 ] +z ⎡⎣⎢0−14⎤⎦⎥ [ 0 − 1 4 ] = ⎡⎣⎢0−14⎤⎦⎥ [ 0 − 1 4 ]

import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x"); ax.set_ylabel("y"); ax.set_zlabel("z")

z11 = [0,2]
z12 = [0,-1]
z13 = [0,0]

z21 = [0,-1]
z22 = [0,2]
z23 = [0,3]

z31 = [0,0]
z32 = [0,-1]
z33 = [0,4]

ax.plot(z11, z12, z13)
ax.plot(z21, z22, z23)
ax.plot(z31, z32, z33)

plt.show()

以上的矩阵是
a non-singular matrix(非奇异矩阵).an invertible matrix(可逆矩阵).三个向量可以表示三维空间所有的点

singular matrix(奇异矩阵),a not invertible matrix(不可逆矩阵)当两个向量在一个平面的时候,有一个向量没有做任何贡献(另外两个向量和以表示这个向量)就成了一个奇异矩阵.三个向量值能表示三维空间的一个二维平面.不是任何b都有解

Ax=b A x = b
multiply a matrix(A) by a vector(x)

1.columns,a column at a time.
as a linear combnination of a column
把方程组看成是向量的组合.(最好用这个方法理解)

2.rows,dot product