R语言与多元统计分析 —— 多元正态分布
1、如何用R语言画二元正态分布的曲面图形
下面主要用两种技术来实现:
注意:z 的列维是 y 的长度,行维是 x 的长度(即 z 包含每一种可能的 (x, y) 点 的值)
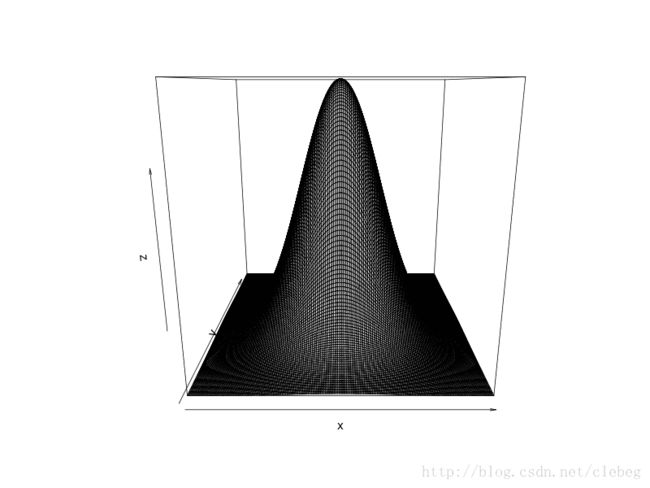
第一种使用 persp(x, y, z)函数:下面看代码
fn = function(x, y) {
sigma <- matrix(c(20,0,0,20), c(2,2))
u <- c(0,0)
sSigma <- solve(sigma)
exp(- ((x-u[1])^2 * sSigma[1,1] + 2*(x-u[1]) * (y-u[2]) * sSigma[1,2] + (y-u[2])^2 * sSigma[2,2]) )/(2*pi*det(sigma)^0.5)
}
a = 10
x = seq(-a, a, 0.1)
y = seq(-a, a, 0.1)
#outer函数就是为每一个点(x,y)得到对应的z 即 z[i,j] = fn(x[i], y[j]),有点类似 matlab 的 meshgrid
z = outer(x, y, fn)
persp(x, y, z)
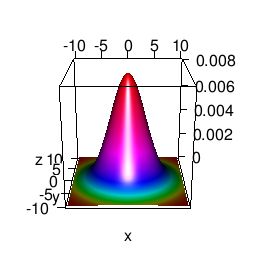
第二种方法是用 rgl,这也是一个画 3D 图的好工具,不过原理还是一样,贴上代码:
fn = function(x, y) {
sigma <- matrix(c(20,0.75,0.75,20), c(2,2))
u <- c(0,0)
sSigma <- solve(sigma)
exp(- ((x-u[1])^2 * sSigma[1,1] + 2*(x-u[1]) * (y-u[2]) * sSigma[1,2] + (y-u[2])^2 * sSigma[2,2]) )/(2*pi*det(sigma)^0.5)
}
a = 10
x = seq(-a, a, 0.1)
y = seq(-a, a, 0.1)
z = outer(x, y, fn)
library(rgl)
zorder = rank(z)
persp3d(x, y, z, col = rainbow(as.integer(max(zorder)))[zorder]) 效果如下: