凸优化(Convex Optimization)浅析

凸优化(Convex Optimization)浅析

在机器学习中,很多情况下我们都需要求得一个问题的全局最优值(global optimum). 大多数的全局最优值很难求得, 但是对于凸问题,我们可以比较高效的找到其全局最优值, 这是由凸问题的性质决定的.我们将逐步的介绍凸集, 凸函数, 凸问题等.

1. 凸集(convex set)

对于一个集合 C ,如果对于任意两个元素 x,y∈C ),以及任意实数 θ∈R 且 0≤θ≤1 都满足

θx+(1−θ)y∈C

那么集合 C 就是凸集.如下图所示:

凸集的例子包括:

• Rn
• 非负象限 Rn+
• 范式球(Norm Ball), 亦即 x:∥x∥≤1 , 其中 ∥⋅∥ 是 Rn 上的范式
• 凸集的交集
• 半正定矩阵

2. 凸函数(convex function)

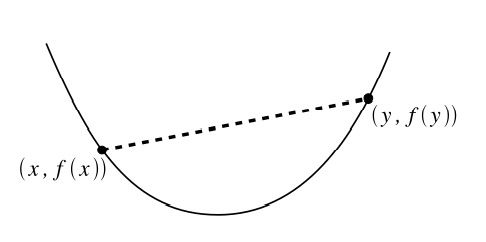
如果一个函数 f:Rn→R 的定义域 D(f) 是凸集, 并且对于所有的 x,y∈D(f) 和 θ∈R,0≤θ≤1 使得:

f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)

则函数 f(x) 是凸函数.

如果把上述限制条件改为对于任意的 x,y∈D(f),x≠y,0<θ<1

f(θx+(1−θ)y)<θf(x)+(1−θ)f(y)

函数 f(x) 是严格凸(strictly convex)的.

如果 −f 是凸的, 则 f 是凹(concave)的.

凸函数如下图所示:

2.1 凸函数的一阶条件

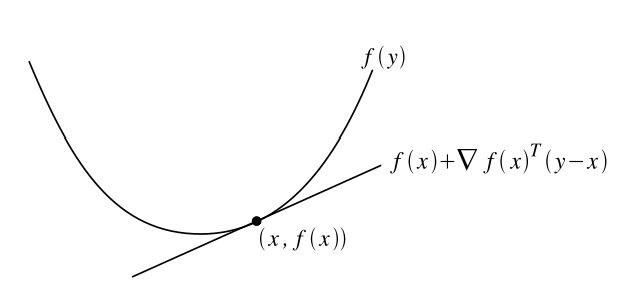
如果一个函数 f:Rn→R 是可微的, 那么 f 是凸函数当且仅当 D(f) 是凸集, 并且对于任意的 x,y∈D(f) :

f(y)>=f(x)+∇xf(x)T(y−x)

其中 f(x)+∇xf(x)T(y−x) 称为 f 在点 x 处的一阶近似. 上述性质如下图所示:

2.2 凸函数的二阶条件

函数 f 是凸的当且仅当 D(f) 是凸集, 并且其Hessian矩阵是半正定的:

∇2xf(x)⪰0

2.3 Jensen不等式

凸函数的定义中有

f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y),0≤θ≤1

上式可以扩展到多个点的情况:

f(∑i=1kθixi≤∑i=1kθif(xi)),∑i=1kθi=1,θi≥0

也可以扩展到无限多个点或者某个区间的情况:

f(∫p(x)xdx)≤∫p(x)f(x)dx,∫p(x)dx=1,p(x≥0)

亦即

f(E[x])≤E[f(x)]

上式称为Jensen不等式

2.4 Sublevel集合

α−sublevel 集合是凸集的一种, 对于一个函数 f:Rn→R , 以及一个实数 α∈R , α−sublevel 集合的定义为

x∈D(f):f(x)≤α

可以很容易的证明上述集合是凸集, 对于 x,y∈D(f) 使得 f(x)≤α,f(y)≤α :

f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)≤θα+(1−θ)α=α

2.5 凸函数例子

指数函数: f:R→R,f(x)=eαx
负对数: f:R→R,f(x)=−logx
仿射函数: f:R→R,f(x)=bTx+c
二次函数: f:R→R,f(x)=12xTAx+bTx+c
范式: f:R→R,f(x)=∥x∥
凸函数的非负加权和:

f(x)=∑i=1kwifi(x)

其中 f1,f2,...,fk 是凸函数

3. 凸优化问题

凸优化问题的形式如下:

minimizef(x)

subjecttox∈C

其中 f 是凸函数, C 凸集, x 是待优化的变量, 我们通常可以把其写成

minimizef(x)

subjecttogi(x)≤0,i=1,...,m

hi(x)=0,i=1,...,p

其中 f 和 gi 是凸函数, hi 是仿射函数.

gi 必须小于等于0, 这样得到的 x 的可行域(feasible region)才是凸的(因为 gi(x)≤0 定义了一个 α−sublevel 集)

3.1 凸问题中的全局最优

凸问题的一个很好地特性是其局部最优解也是全局最优解.推导如下

首先定义局部最优解: 当 x 是可行的(亦即位于可行域内), 而且存在 R>0 , 使得对于所有 ∥x−z∥2≤R 的位于可行点 z ,使得 f(x)≤f(z) .

然后定义全局最优解: 如果 x 是可行的, 且对于其他所有的可行点 z 都有 f(x)≤f(z)

凸问题中的全局最优解等同于局部最优解, 证明如下:

令 x 是一个局部最优解, 但不是全局最优解, 所以存在一个可行的点 y 使得 f(x)>f(y) .根据局部最优解的定义, 没有一个可行点 z 满足 ∥x−z∥2≤R,f(z)<f(x) . 但是, 我们可以选择

z=θy+(1−θ)x,θ=R2∥x−y∥2

那么

∥x−z∥2=∥x=(R2∥x−y∥2y+(1−R2∥x−y∥2)x)∥2

=∥R2∥x−y∥2(x−y)∥2

=R/2≤R

另外, 因为 f 是凸函数, 所以

f(z)=f(θy+(1−θ)x)≤θf(y)+(1−θ)f(x)<f(x)

因为可行域是凸集, x , y 都是可行的, 所以 z=θy+(1−θ)x 也是可行的, 且 ∥x−z∥2<R,f(z)<f(x) , 假设不成立，所以 x 是全局最优解.

3.2 凸问题的例子

线性规划(LP, Linear Programming):

minimizecTx+d

subjecttoGx⪰h

Ax=b

二次规划(QP, Quadratic Programming):

minimize12xTPx+cTx+d

subjecttoGx⪰h

Ax=b

二次限制的二次优化(QCQP, quadratically constrained QP):

minimize12xTPx+cTx+d

subjectto12xTQix+rTix+si≤0,i=1,...,m

Ax=b

半定规划(Semidefinite Programming):

minimizetr(CX)

subjecttotr(AiX)=bi,i=1,...,p

X⪯0

参考文献:

[1]. Zico Kolter, Honglak Lee. Convex Optimization Overview.

[2]. Stephen Boyd, Lieven Vandenberghe. Convex Optimization.

声明：

本文转载自凸优化(Convex Optimization)浅析——博客园kemaswill.对原作者的付出表示感谢.版权归原作者所有.