无人驾驶的规划与控制(二)——行为决策规划
文章目录
- 1 无人驾驶行为决策需要哪些信息
- 2 有限状态马尔科夫决策过程
- 2.1 马尔科夫决策定义
- 2.2 寻找最优策略
- 2.3 使用MDP的困难
- 3 基于场景划分设计行为决策
- 3.1 分治的核心思想
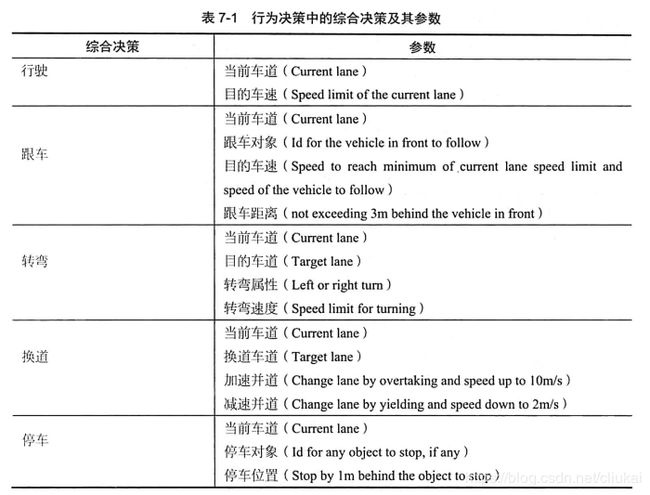
- 3.2 综合决策
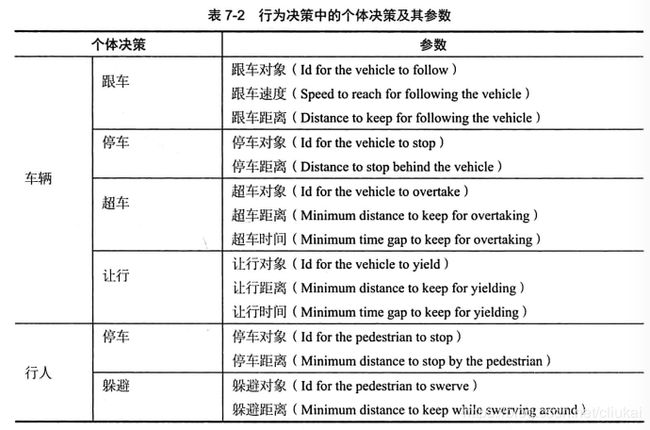
- 3.3 个体决策
- 3.4 场景划分和决策系统框架
1 无人驾驶行为决策需要哪些信息
- 路由寻径的结果:车辆需要进入的车道是什么(target lane)。
- 无人车自身状态:GPS位置,速度,朝向,所在车道,是否正在变道等等。
- 历史决策信息:再上一个行为决策周期中,无人车所作出的决策是什么?跟车,停车,转换或是换道?
- 周边障碍物信息:障碍物车辆所在的车道,速度,位置,以及短时间内他们的行为预测和轨迹预测。
- 交通标识信息:是否有红绿灯,斑马线,停车线。
- 交通规则信息:当前道路限速,车道禁行限制等。
2 有限状态马尔科夫决策过程
2.1 马尔科夫决策定义
一个马尔科夫决策过程,由五元组定义:
( S , A , P a , R a , γ ) (S, A, P_a, R_a, \gamma ) (S,A,Pa,Ra,γ)
- S代表了无人车所处的有限的状态空间。形如一个包含了车道,环境和本身的珊格世界模型(我的世界)。
- A代表了无人车的行为 决策空间,即无人车在所有状态下行为(behavior)空间的集合:包含跟车Follow,换道Change Lane,左转右转Turn Left/Right,停车Stop等。
- P a ( s , s ′ ) = P ( s ′ ∣ s , a ) P_a(s,s')=P(s'|s,a) Pa(s,s′)=P(s′∣s,a)是一个条件概率(Probability),代表无人车在状态s和动作a的条件下,达到下一个状态s’的概率。
- R a ( s , s ′ ) R_a(s,s') Ra(s,s′)是一个激励函数(Reward),代表了无人车在动作a下,从状态s跳转道s’得到的激励。
- γ ∈ ( 0 , 1 ) \gamma\in(0,1) γ∈(0,1)是一个激励的衰减因子,当前的激励系数为1,下一个时刻为 γ \gamma γ,下两个时刻为 γ 2 \gamma^2 γ2,一次类推,含义是当前的激励总是比未来的激励重要。
2.2 寻找最优策略
在上述MDP定义下,无人车行为决策需要解决的问题就是寻找一个最优策略 π : S → A \pi:S\to A π:S→A。选取目标是:最大化从当前时间点,到未来的累计激励,即
∑ t = 0 ∞ γ t R a ( S t , S t + 1 ) , 其 中 a c t i o n 是 由 策 略 π 产 生 : a = π ( s ) \sum_{t=0}^{\infty}{\gamma^t{R_a}(S_t,S_t+1)},其中action是由策略\pi产生:a=\pi(s) t=0∑∞γtRa(St,St+1),其中action是由策略π产生:a=π(s)
在上述马尔科夫决策过程定义下,最优策略可以用动态编程(Dynamic Programming)方法求解。假设转移矩阵P和激励分布R是已知的,最优策略的求解则基于一下两个数组的不断计算和存储:
π ( s t ) ← argmax a { ∑ s t + 1 P a ( s t , s t + 1 ) ( R a ( s t , s t + 1 ) + γ V ( s t + 1 ) ) } V ( s t ) ← ∑ s t + 1 P π ( s t ) ( s t , s t + 1 ) ( R π ( s t ) ( s t , s t + 1 ) + γ V ( s t + 1 ) ) \begin{array}{l}{\pi\left(s_{t}\right) \leftarrow \underset{a}{\operatorname{argmax}}\left\{\sum_{s_{t+1}} P_{a}\left(s_{t}, s_{t+1}\right)\left(R_{a}\left(s_{t}, s_{t+1}\right)+\gamma V\left(s_{t+1}\right)\right)\right\}} \\ {V\left(s_{t}\right) \leftarrow \sum_{s_{t+1}} P_{\pi\left(s_{t}\right)}\left(s_{t}, s_{t+1}\right)\left(R_{\pi\left(s_{t}\right)}\left(s_{t}, s_{t+1}\right)+\gamma V\left(s_{t+1}\right)\right)}\end{array} π(st)←aargmax{∑st+1Pa(st,st+1)(Ra(st,st+1)+γV(st+1))}V(st)←∑st+1Pπ(st)(st,st+1)(Rπ(st)(st,st+1)+γV(st+1))
其中,数组 V ( S t ) V(S_t) V(St)代表了未来衰减叠加的累计期望激励, π ( S t ) \pi(S_t) π(St)代表需要求解的策略。
具体求解过程是在所有可能的状态s和s’之间进行重复迭代计算,直到二者收敛为止。
2.3 使用MDP的困难
利用MDP解决无人车行为决策最关键的部分就是激励函数(Reward)的设计,在设计Reward函数时,要尽可能考虑这些因素:
- 到达目的地:无人车应该根据寻径路线前进,如果选择的动作 a = π ( s ) a=\pi(s) a=π(s)导致偏离既定的寻径路线,则给予适当的惩罚。
- 安全性和避免碰撞:原理碰撞的栅格应该得到奖励,接近碰撞栅格时,应该给予惩罚。
- 乘坐舒适性和下游执行的平滑性。
因为利用马尔科夫概率模型的MDP需要非常细致地设计诸如状态空间、转移概率和激励函数等参数,这些在工业应用上一般不可行。更可靠的设计应该是,基于规则来构建宏观行为决策系统:利用场景分割无人车周边环境,通过构建子场景并Rule运用。
3 基于场景划分设计行为决策
3.1 分治的核心思想
利用分治的原则,将无人车周边的场景进行划分。每个场景独立运用相应的规则来计算无人陈对每个场景中元素的决策行为,再将所有划分的场景的决策进行综合,得到一个最后综合的总体行为决定。
首先引入几个重要概念:综合行为决策(Synthetic Decision)、个体行为决策(Individual Decision),以及场景(Scenario)。
3.2 综合决策
综合决策是行为决策层面的最高决策,决策的指令状态空间需要和下游的动作规划(Motion Planning)协商一致,使得做出的综合决策指令,可以让下游规划出路线轨迹(Trajectory)。为了便于下游直行,综合决策的指令集往往带有具体的指令参数数据,如表所示:
3.3 个体决策
这里的个体,包含车辆和行人,也包含红绿灯和停车线。
最终的综合决策,是先经过场景的划分,产生每个场景下的个体决策,再综合考虑归纳这些个体决策,最终得到综合决策。
传递个体决策有两个好处:
- 帮助下层模块更有效地实现路径规划。
- 需要调试解决问题时,传递过来的个体决策能够大大提高调试效率。
例如,在针对某个障碍物车辆进行超车这一个体决策时,附加参数包括:
- 超车距离:本车的车身要超过前车的车头的最小距离。
- 超车时间:这段超车距离要行驶的最小安全时间间隔。
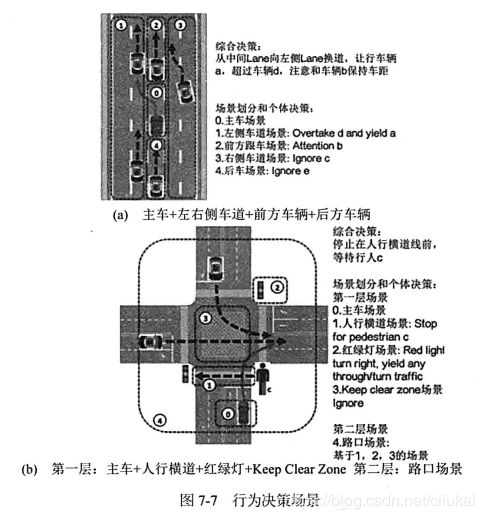
3.4 场景划分和决策系统框架
在(a)图中,无人车意图是向左换道,此时包含了3个场景:
- 左侧车道:车辆a和d在左侧车道行驶,无人车需要先让a通过,然后在d车之前换道。
- 当前车道:我车虽然在换道,但同时需要注意前车b,后车e可以ignore。
- 右侧车道:右侧车道的c车正在向左变道,可以ignore。
在(b)图中,稍微复杂一些,包含了2层场景:
- 我车 + (1)人行横道 + (2)红绿灯 + (3)Keep Clear Zone(ignore)
- 路口场景:基于(1)(2)(3)的场景。
假设此时无人车意图是右转,红绿灯可以右转,但是没有道路优先权需要避让直行车,又感知到了一个行人正在人行横道上横穿马路。结合这些场景元素和意图,最终的指令是:针对行人在人行横道前停车。
综上所属,每个场景根据自身的业务逻辑(Business Logic)计算不同个体的决策,通过场景复合,以及对所有决策的综合考虑,得到一个安全决策。整体决策模块系统框架和流程如下:
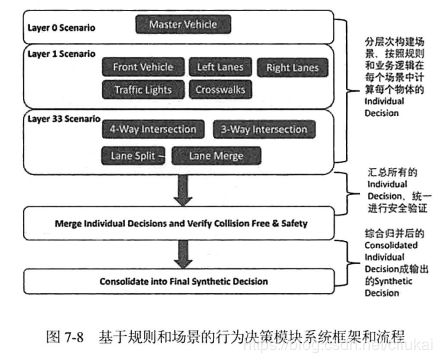
大致分4个步骤:
- 结合我车状态,地图数据,感知结果构建不同层次的场景。
- 每个场景根据自身规则(交通法规,安全避让),计算出每个场景的个体决策。
- 检查各个场景有无冲突,并解决(安全验证)。
- 在统一的时空里,推演所有决策能否汇总成安全无碰的综合决策,最后发送给动作规划模块。
参考文章
《第一本无人驾驶技术书》刘少山