光线跟踪之 视窗与投影变换
2016-05-03
本篇的重点:
- 虚拟相机成像过程
- 缩放
- 倾斜角
这是小孔成像,是我们眼睛的成像原理的示例,只不过,最终是投影在一个球体内部的曲面上的。如果我们要使用程序来模拟这个过程,就需要把这个过程稍微简化一下。如下图所示。
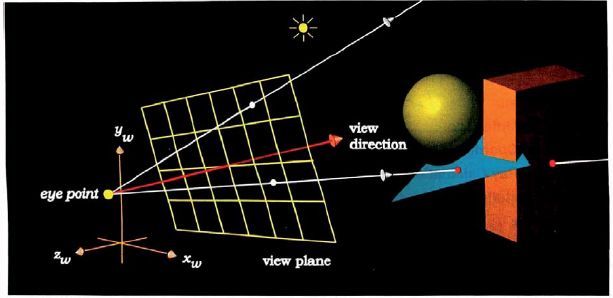
这幅图表示了ray tracer的工作原理。从eye 发出的视线,通过view plane 6×4个像素,我们将得到一张很小的图片。如果我们要看的更加清楚一些,就需要增加view plane像素点,但是算法复杂度是O(n^2)。OpenGL的实现中,也是采用这样的方式。在指定眼睛、view plane坐标时,使用的都是世界坐标系。一般而言,视线垂直穿过view plane的中心(如果不是中心呢?如果不是垂直通过呢?那么就会产生shear效果。不过,我们一般不会使用到。不用管了)。同时需要指定的是人眼(或者camera) 的pose(姿态),如头顶的方向up,我们需要以up, view direction来构建eye space这个局部坐标系。在局部坐标系中,z轴一般固定为view direction的反方向, up × z 得到 x 轴向量,再次x × z 得到 y 轴向量,这样就ok了。
一般而言,我们在程序中都是把三维场景投影到有限平面区域 view plane 上,形成了一张离散的二维图像。但是,这个过程和我们眼睛看到真实世界的物体形成图像的过程是不一样的。我们的眼睛,类似于传统的胶片相机,是这样工作的。获取的信号是连续的。我们可以把给定大小的view plane 分割的非常细,得到一张分辨率巨大的、带有高精度细节的图片,但是,大多数情况下,这是没有意义的(超过了眼睛分辨能力的极限)。
Q:为什么不让view direction 成为 w 轴呢,而是取相反的方向?
[1] 的 156面有讲解。 简单来说,就是计算从眼睛发出的光线的计算过程会简单一些。view plane上像素点坐标的计算就会变为从左往右,符合习惯。我们有一个默认的假设,就是w 向量是 eye - lookat, 而且, 垂直通过view plane 的重心。
Q:为什么要指定眼睛局部坐标系呢?这会给实际程序带来什么影响呢?
我们可以看到,第一篇文章中的实例程序就没有给出眼睛局部坐标系。第一篇中我们view plane 是以世界坐标的位置给出的,是固定,你无法左右上下摆头。其实,真实情况不是这样的,我们需要随时换个视角。
Q: 为什么不把up 方向指定为 局部坐标系的y轴?
这样的话就相当于上面的模型是固定的。想象一下,上下摆头时,视线焦点只能同时上下移动,这就满足不了要求。有时候,我们头上下摆,眼睛却盯着一点不懂,视野范围会发生变化。我们眼睛的工作模式就是这样。(不过,up 不是y轴的情况比较少,也无需过多关注了)
在OpenGL中,world coordinate 被全部转换到了眼睛局部坐标系,但是,在光线追踪程序中就不需要这么做。 我们可以反着来,所有的计算最终都是在世界坐标系中完成的。在OpenGL中,是把一个个单独的obj 投影到view plane 时,反求投影到pixel (m, n) 处对应 图元中世界坐标的pos,这时才根据triangle 三个顶点坐标做插值计算,但是多个obj 之间是没有关联的。在光线追踪的程序中,是把view plane 上的点投影到world coordinate 中成为一条射线,用来和多个obj进行计算。
我们学素描的时候,基本上会接触到一点透视,两点透视,三点透视,而计算机图形学里面也会模拟“鱼眼透视“,在这里,我们仅仅实现最简单、最常使用的一点透视。难度不会大的。
Q: view plane 大小固定的情况下,要得到视椎体(frustrum),需要指定eye 到 view plane 的distance,还是指定视野上下的夹角呢?
【1】中使用distance,获取view plane 的宽高,易计算视野角度,而且distance 更加直观一些。
Q: 怎样判断物体是否在视椎体内?
intersection 到 eye 的距离小于 eye 到 view plane的视线长度。 规定视锥体远平面,是为了把太远的,看不到的物体剪裁掉,在实例程序中暂时就不要在意这个限制了。
Q: lookat 是什么概念?
lookat 是用来求解eye space局部坐标系的,与eye坐标一起求局部坐标的z 轴。
Vector w = pointDifference(eye, lookAt);
Vector normalizedW = normalize( w ); // 局部坐标系的z轴,
// 从这里看,只要lookat 在 w轴上,对于以后的计算就没有影响,所以准确来讲,这个lookat 不是世界坐标系中一个点,是view direction 向量上的任一点
// 如果以齐次坐标系来看,那还算是一个无穷远处的点
我们可以参考OpenGL实现gluLookAt 的方式,以此来分析一下这个过程。
glViewport (0, 0, (GLsizei) w, (GLsizei) h); (OpenGL中非必须, w,h 默认是窗口的大小)类似的过程在软件渲染器中是必须显式指定的。
void gluLookAt( GLdouble eyex, GLdouble eyey, GLdouble eyez,
GLdouble centerx, GLdouble centery, GLdouble centerz,
GLdouble upx, GLdouble upy, GLdouble upz ), 指定view plane 的中心
void gluPerspective(GLdouble fovy, GLdouble aspect,GLdouble zNear,GLdouble zFar)
来解释一下gluPerspective:
fovy: 指定视景体的视野的角度,以度数为单位,y轴的上下方向
aspect:指定你的视景体的宽高比(x 平面上)
zNear: 指定观察者到视景体的最近的裁剪面的距离(必须为正数)
zFar: 指定观察者到视景体的最远的裁剪面的距离(必须为正数)
实际上,OpenGL中view plane的形状是根据上面函数的参数指定,首先指定“fovy”(眼睛睁开的角度), 如果无限接近于pi,那么view plane 就是无限大了,也就是无限大的平面被压缩到w * h 的区域内,一切的物体都趋近于无限小。 如果fovy趋近于无限小,相当于你从类似于针状的椎体窥视远处,view plane 被压缩到针状椎体内部, 物体与圆锥体相交的那一小块区域被投影到view plane,所以,你看到了物体很小区域的细节,就相当于放大了物体细节。这就是缩放效果了。
glu的gluPerspective()函数是对OpenGL基础函数glFrustum()的封装。
gluLookAt 构建了eye space, 和 gluPerspective() 的关系呢?
gluLookAt creates a viewing matrix derived from an eye point, a reference point indicating the center of the scene, and an UP vector.
The matrix maps the reference point to the negative z axis and the eye point to the origin. When a typical projection matrix is used, the center of the scene therefore maps to the center of the viewport. Similarly, the direction described by the UP vector projected onto the viewing plane is mapped to the positive y axis so that it points upward in the viewport. The UP vector must not be parallel to the line of sight from the eye point to the reference point.
翻转效果的实现:
这个就比较简单了,想象一下我们斜着脑袋观察外界。这和我们在渲染器中斜着观察的结果是一致的,只是我们主观上的感觉不一致而已。虽然我们歪着脑袋,我们也不会认为看到的东西是倾斜的,一是因为我们的视野足够大,二是因为我们大脑自动处理了视觉效果,认为物体还是正常的。
不得不吐槽一下OpenGL状态机的工作方式,对于初学者而言,这绝对是很违反直觉的工作方式。而且,OpenGL 有不少默认值,如果你在学习的时候,没有理解默认值,就会忽略掉,绝对会给自己对整个过程的理解带来困难。在没有弄明白整个渲染流程的情况下使用 OpenGL会浪费不少时间的。所以,即使是只想使用OpenGL的同学,也最好首先学习一下光线追踪,顶多花费十几个小时的时间来熟悉吧。 不要求能够实现,只要求能够弄明白工作原理和OpenGL本身的工作方式。
ref:
- Ray Tracing from the Ground Up chapter 8、9
- https://www.opengl.org/sdk/docs/man2/xhtml/gluPerspective.xml
- https://www.opengl.org/sdk/docs/man/html/glViewport.xhtml
- https://www.opengl.org/wiki/GluPerspective_code
- http://blog.csdn.net/kesalin/article/details/7168967 good
- http://www.cs.brandeis.edu/~cs155/Lecture_08_6.pdf
- http://www.ogldev.org/www/tutorial13/tutorial13.html
- https://www.opengl.org/sdk/docs/man2/xhtml/gluLookAt.xml
[ 主页]