吴恩达深度学习课程笔记（二）：改善深层神经网络

吴恩达深度学习课程笔记（二）：改善深层神经网络

第一周 深度学习的实用层面

1.1 训练 / 开发 / 测试集

• 应用机器学习算法是一个高度迭代的过程。从一开始的idea，一直要进行不断的尝试、更新。超参数的选择就在这个不断地迭代尝试过程中产生。
• 创建高质量的训练集、验证集、测试集有助于提高迭代效率。
  
  • 训练集训练几个模型；验证集选出最好的模型；在测试集上评估该模型的性能。
  • 在小数据时代，可以60%/20%/20%;
  • 在大数据时代，验证集和测试集的比例更小；比如1 000 000 条数据，可能取10000条进行验证即可。

• 训练集和测试集分布不匹配的情况很多：

  • 训练猫咪图像分类，训练集图片来组互联网，高清，制作精良；验证集和测试集图像来自用户手机拍摄，质量差，像素低，模糊；
  • 经验：确保验证集和测试集的数据来自同一分布。
  • 经验：就算没有测试集也ok，测试集的目的是对最后的模型做出无偏的评估，但是如果不需要无偏的评估，就可以不设置测试集。

• 如果没有测试集，仅有训练集和验证集，那么这个时候验证集被有些人们称之为测试集，但其实这个“测试集”起到的是验证集的作用。所以叫做测试集是错误的。只有两个划分的时候，就只有训练集和验证集。

• 验证集和测试集可以加速神经网络的集成。也可以更有效的衡量算法的偏差和方差。

1.2 偏差 / 方差

通过训练集的误差和验证集的误差查看：

存在高偏差高方差的情况：

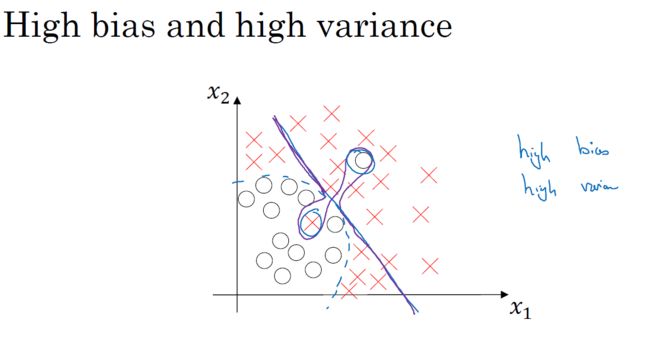
上述结论是在基础误差很小的情况下成立的。

1.3 机器学习基础

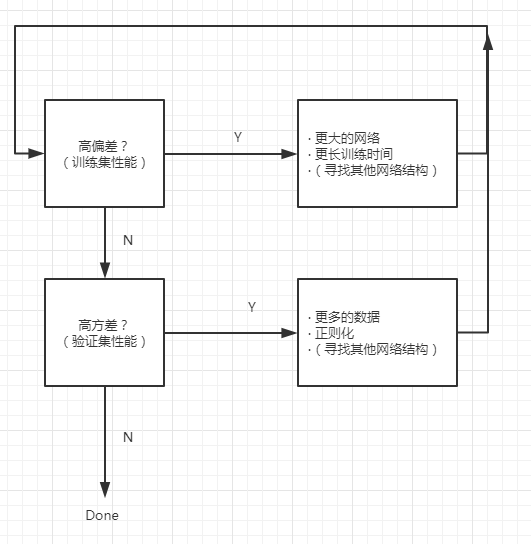
• 用训练集和验证集检测模型是否存在高偏差or高方差问题。
• 机器学习早期存在方差偏差平衡问题。
• 在大数据和深度学习时代，可以做到只降低偏差（方差），而基本不影响方差（偏差），即在降低一方的同时，不过多影响另一方。比如：
  
  • 适度正则化的情况下，更大的network可以在不影响方差的情况下降低偏差；
  • 用更多的数据训练网络能够在不过多影响偏差的情况下降低方差。

在大数据和深度学习时代，不用过多关心如何平衡偏差和方差。这是大数据和深度学习带来的一个益处。
在网络比较规范的情况下，训练一个更大的网络的主要代价也只是计算时间(or算力)。其他负面影响很小。

1.4 正则化

regularization

• 逻辑回归：
  J(w,b)=1m∑mi=1L(y^(i),y(i))+λ2m||w||22 J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) + λ 2 m | | w | | 2 2

  L2 L 2 正则化： λ2m||w||22 λ 2 m | | w | | 2 2 ，其中， ||w||22=∑nxj=1w2j=wTw | | w | | 2 2 = ∑ j = 1 n x w j 2 = w T w

  L1 L 1 正则化： λ2m||w||1=λ2m∑nxj=1|wj| λ 2 m | | w | | 1 = λ 2 m ∑ j = 1 n x | w j | ； L1 L 1 正则化之后的 w w 是稀疏的。
  

• 神经网络：

  J(w[1],b[1],w[2],b[2],...,w[L],b[L])=1m∑mi=1L(y^(i),y(i))+λ2m∑Ll=1||w[l]||2F J ( w [ 1 ] , b [ 1 ] , w [ 2 ] , b [ 2 ] , . . . , w [ L ] , b [ L ] ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) + λ 2 m ∑ l = 1 L | | w [ l ] | | F 2

  L2 L 2 正则化： λ2m∑Ll=1||w[l]||2F λ 2 m ∑ l = 1 L | | w [ l ] | | F 2 ，其中， ||w||2F=∑n[l]i=1∑n[l−1]j=1w2ij | | w | | F 2 = ∑ i = 1 n [ l ] ∑ j = 1 n [ l − 1 ] w i j 2
  则：
  dw[l]=∂J∂w[l]+λmw[l] d w [ l ] = ∂ J ∂ w [ l ] + λ m w [ l ]
  那么：
  w[l]=w[l]−αdw[l]=w[l]−α（∂J∂w[l]+λmw[l]）=（1−αλm）w[l]−α∂J∂w[l] w [ l ] = w [ l ] − α d w [ l ] = w [ l ] − α （ ∂ J ∂ w [ l ] + λ m w [ l ] ） = （ 1 − α λ m ） w [ l ] − α ∂ J ∂ w [ l ]
  即正则化与没有正则化相比，就是在 w[l] w [ l ] 更新的时候减去了一个 αλmw[l] α λ m w [ l ] ，也就是为原来 w[l] w [ l ] 的 1−αλm 1 − α λ m 倍。

1.5 为什么正则化可以减少过拟合？

如果将 λ λ 取得非常大，那么很多 w w 接近于0，也就是网络变得更加简单，这样会从高方差（过拟合）导致到高偏差（欠拟合）。
但是 λ λ 适中的时候，我们会减少很多隐藏单元的影响，神经网络变得更简单，不容易发生过拟合。但也不会简化到欠拟合的程度。
直观理解：
如果 w w 在一个很小的区间，那么最后的 z z 也很小，经过激活函数的时候一直在其线性部分，如果整个网络都是这样，那么实际上，这就是个线性分类器。非线性的部分很少。也就是说，如果 w w 的范围小，那么网络去拟合数据集的非线性决策边界的能力就弱，不容易发生过拟合。

1.6 Dropout 正则化

dropout是一种正则化方法。
能防止过拟合。
除非算法过拟合，不然不使用dropout。

dropout：以一定概率随机删除网络中的神经单元。让每次训练的网络都不同。防止过拟合的问题。

dropout有很多种。
inverted dropout (反向随机失活)：
训练阶段：
以神经网络的第三层为例： l=3 l = 3

keep_prob = 0.8  # 保留80%的节点，删除20%的节点。
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob  # d3，第三层的dropout矩阵，a3，第三层的输出。
a3 = np.mutiply(a3, b3)  # a3 *= b3，点乘
a3 /= keep_prob # 保持a3的期望和与dropout之前相比，不发生变化

a3 /= keep_prob这一步，保持了a3的期望不变，所以和不除相比，在测试阶段变得更容易，因为平均值不会发生太大变化。
inverted dropout 最常用。
测试阶段：
测试阶段不使用dropout，所以在训练阶段除以keep_prob的意义就在于此。即让训练阶段和测试阶段的激活函数的预期结果不要发生太大变化。

1.7 理解 Dropout

对下一层的神经单元来说，上一次神经单元就是这个神经单元的输入。
因为神经单元的输入随时有可能被删除，所以该神经单元不能依赖于某一个特定的单一特征，必须将权重在所有特征上分配，也就是传播权重。
dropout的效果就是：收缩权重的平方范数。即：压缩权重。正则化，防止过拟合。
功能上类似L2正则化，不同之处是应用的方式不同，dropout也会有相应变化。更适用于不同的输入范围。

• keep_prob=1，即没有dropout正则化；
• 对输入层，即输入特征，一般不使用dropout，即keep_prob=1，即使使用，keep_prob的值也接近1；
• 不同层的keep_prob可以不同：
  
  • 对比其他层更容易发生过拟合的层，keep_prob可以设置的小一些；
  • 对不太可能出现过拟合或者程度小的层，keep_prob可以设置的大一些，甚至是1；
• 将不同层的dropout的keep_prob设置成不一样的，这样做的缺点是：为了使用交叉验证，必须寻找更多的超参数。
• 另一种方案是：
  仅对一部分层设置dropout，其他层不设置，且这些设置dropout的层用同一个keep_prob值。

dropout的缺点：
代价函数J没有办法去明确定义。因此，我们失去了调试工具，没有办法绘制梯度下降迭代的J的下降曲线。
- 解决办法：
先将keep_prob=1，即关闭dropout，待模型的代价函数的曲线下降后，再打开dropout。

1.8 其他正则化方法

1. 数据增强
   比如讲图像数据集的训练集数据图像都水平翻转一次。
   因为数据有冗余，所以没有加入新的数据集那么好，但比起新加数据集，节省了很多成本和时间。
   对图像：随机翻转、裁剪等手段增大数据集。
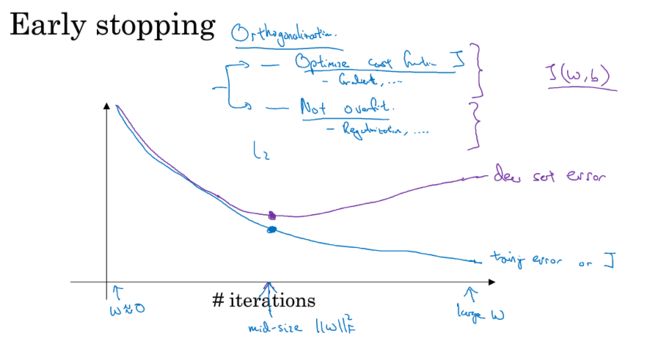
   对字符：随意旋转、扭曲字符。
2. 早停法
   
   • 优点：耗费时间少
   • 缺点：验证集J和训练集J的差距比较小的地方，偏差有可能很大。早停法一种方法必须兼顾两种问题，没有办法分开解决。
   • 如果不用早停法解决问题，那么使用L2正则化，则神经网络的训练时间就长。同时需要花时间去选择正则化参数 λ λ 的值。
     

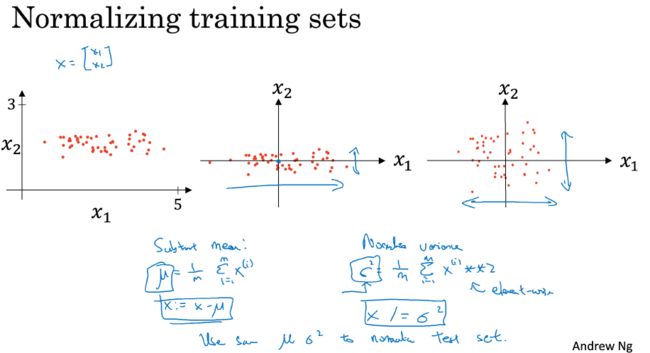
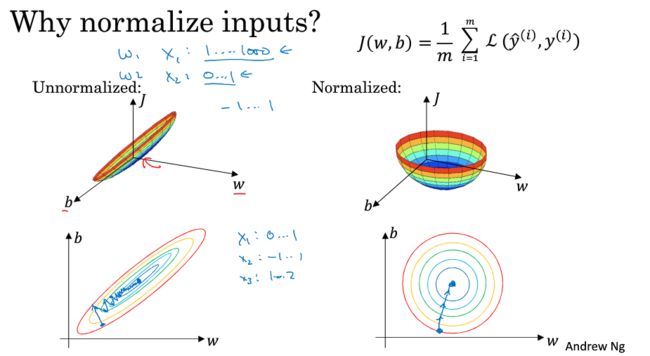
1.9 归一化输入

Normalizing inputs
训练集数据算出 μ μ 和 σ2 σ 2 ；
用 μ μ 和 σ2 σ 2 对整个数据集（训练集、验证集、测试集）进行归一化；

• 为什么要归一化？
  如果不归一化，代价函数有可能就是一个非常细长狭窄的函数。归一化后的代价函数图像个更加对称。
  对前者，梯度下降不得不用更小的学习速率。
  对后者，梯度下降能更直接的找到最小值。可以使用较大的步长。
  
  

1.10 梯度消失与梯度爆炸

• 参考资料：
  详解机器学习中的梯度消失、爆炸原因及其解决方法

梯度消失和梯度爆炸在本质上是一种情况。

梯度消失经常出现在深层网络和采用了不合理的损失函数之时，如sigmoid；
梯度爆炸经常出现在深层网络和权重初始化值太大之时。

• 深层网络角度：
  BP过程中，由链式法则，对激活函数的导数大于1，不断的相乘，最终导致梯度爆炸；
  对激活函数的导数小于1，不断的相乘，最终导致梯度消失；
  梯度爆炸和消失的根本原因就是反向传播算法的先天不足导致的。

• 激活函数角度
  sigmoid函数的导数最大不超过0.25，选择这样的激活函数很容易导致梯度消失；
  tanh比sigmoid略佳，但导数仍然小于1；

• 解决办法：

  • 预训练+微调：
    
    • 单独训练每一隐层，微调后，再BP，很少使用；
  • 梯度裁剪：
    
    • 主要针对梯度爆炸 ，设置梯度阈值，把超过阈值的梯度强制限制在范围内；
  • 权重正则化：
    
    • 可以减少梯度爆炸的概率；
  • 激活函数：
    
    • relu，在>0的部分导数恒为1；解决梯度消失和梯度爆炸的问题；
      优点：
      解决梯度爆炸、梯度消失；
      计算方便、速度快；
      加速网络的训练。
      缺点：
      输出不是以0为中心的；
      负数部分导数恒为0，会导致一些神经元无法激活。
    • leaky relu:
      包含relu的优点；
      解决relu的缺点；
    • elu:
      比leaky relu计算耗时
  • BN：bacth normalization, 批规范化
  • 残差结构
  • LSTM

1.11 神经网络的权重初始化

权重初始化是对一开始的 w w 进行初始化的技巧，可以减缓梯度消失和梯度爆炸。属于加快训练速度的技巧之一。
思想是，神经元的输入越多，所有的随机化的 wi w i 乘以 xi x i 的之和就越大。为了不变大，将 w w 的方差减小。即 w w 的方差为 1/n 1 / n
权重初始化，即对随机生成的 w w 的方差进行初始化。
W_l=np.random.randn((l_n, L_n_1))*np.sqrt(1/n)
在实际操作过程中，针对不同的激活函数， w w 有不同的方差。
- relu：
2n[n−1] 2 n [ n − 1 ]
w[l]=np.random.randn(shape)∗np.sqrt(2n[n−1]) w [ l ] = n p . r a n d o m . r a n d n ( s h a p e ) ∗ n p . s q r t ( 2 n [ n − 1 ] )
- tanh:
1n[n−1] 1 n [ n − 1 ] 或者 2n[n−1]+　n[n] 2 n [ n − 1 ] + 　 n [ n ]
w[l]=np.random.randn(shape)∗np.sqrt(1n[n−1]) w [ l ] = n p . r a n d o m . r a n d n ( s h a p e ) ∗ n p . s q r t ( 1 n [ n − 1 ] )
w[l]=np.random.randn(shape)∗np.sqrt(2n[n−1]+　n[n]) w [ l ] = n p . r a n d o m . r a n d n ( s h a p e ) ∗ n p . s q r t ( 2 n [ n − 1 ] + 　 n [ n ] )

以上就是初始化权重矩阵 w w 的方差的默认值。
在这些默认的方差效果不理想的情况下，可以调整方差的分子(算是一个超参数)——方差参数。在神经网络的众多超参数中，调整该参数的优先级很低。

1.12 梯度的数值逼近

双边误差比单边误差精确度更高，梯度的数值逼近一般用双边误差。

1.13 梯度检验

gradient checking
grad check
用梯度检验检查一个神经网络反向传播的正确与否。


dΘ[i]approx=J(…，θi+ϵ，…)−J(…，θi−ϵ，…)2ϵ d Θ a p p r o x [ i ] = J ( … ， θ i + ϵ ， … ) − J ( … ， θ i − ϵ ， … ) 2 ϵ

||dΘapprox−dΘ||2||dΘapprox||2+||dΘ||2 | | d Θ a p p r o x − d Θ | | 2 | | d Θ a p p r o x | | 2 + | | d Θ | | 2
取 ϵ=10−7 ϵ = 10 − 7
如果结果约等于 10−7 10 − 7 ，那么认为梯度没有问题。
如果大于了，可能就有bug。

1.14 关于梯度检验实现过程中的注意事项

1. 不能在训练时使用梯度检验，——仅用于dubug；
2. 如果梯度检验结果很大，检查每一项去找到bug；
3. 不要忘记正则化部分，也是 \theata \theata 的一部分；
4. 不要在dropout的网络上使用梯度检验，因为dropout很难计算代价函数 J J ，没办法去使用梯度检验。也就是，将dropout的keep_prob = 1,再进行梯度检验。
5. （很少用）在一开始初始化网络参数后，即进行一次梯度检验；在网络训练一段时间后，再进行一次梯度检验。因为一开始 w w 和 b b 比较小，梯度下降是正确的，随着 w w 和 b b 越来越大，梯度下降有可能出错。

第二周 优化算法

优化算法帮助你快速训练模型。

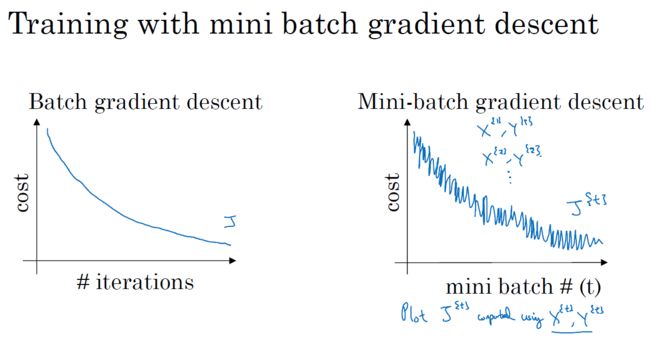
2.1 Mini-batch 梯度下降法

数据集分成若干个小的子集，每个子集叫一个mini-batch。每次训练神经网络，只用一个mini-batch，可以加快网络的训练速度。
x(i) x ( i ) ，第 i i 个样本；
z[i] z [ i ] ，第 i i 层神经网络；
X{i}， X { i } ， 第 i i 个mini-batch，每一个mini-batch都有很多个样本；
必然要引入for循环，为了训练完所有的mini-batch。

• 1 epoch：遍历了一遍训练集。
• 如果采用梯度下降（又叫batch gradient descent），1 epoch只有一次梯度下降。
• 如果采用Mini-batch 梯度下降法，1 epoch有5000次梯度下降（每个mini batch有1000个数据，整个训练集有500 0000个数据）。
• 一般的，需要多次遍历训练集。直到收敛到合适的精度。
• mini-batch 梯度下降 比 batch 梯度下降 快。

2.2 理解 mini-batch 梯度下降法

与batch gradient descent相比，mini-batch gradient descent的学习曲线没有那么平滑，有很多噪声，但总体趋势应该也是不断降低向下。

选择mini-batch size：

• 如果mini-batch size=m：batch gradient descent——批梯度下降 (X{1},Y{1})=(X,Y) ( X { 1 } , Y { 1 } ) = ( X , Y ) ，单次迭代耗时太长。
• 如果mini-batch size=1：stochastic gradient descent——随机梯度下降，每一个样本就是一个mini-batch。 (X{i},Y{i})=(x(i),y(i)) ( X { i } , Y { i } ) = ( x ( i ) , y ( i ) ) ，失去向量化带来的加速作用，效率低。
• 1 << mini-batch size << m，mini batch gradient descent——mini-batch 梯度下降，介于梯度下降和随机梯度下降之间。mini-batch size not too big, not too small——>学习速率最快。
  
  • 首先，大量的向量化数据；
  • 其次，不用等整个数据集都计算后再梯度下降，单次迭代耗时短。

batch梯度下降：

• 相对噪声低；
• 幅度大( α α )；
• 训练下降方向指向最小值方向；
• 最终能收敛到最小值。

随机梯度下降：

• 噪声比较大；
• 为了抑制噪声，学习速率 α α 要设置的小一些；
• 每次训练的下降方向不一定是指向最小值的方向；
• 永远无法收敛，但是会在最小值附近波动；

mini-batch 梯度下降：

• 每次下降方向不总是指向最小值方向，但比随机梯度下降要更持续地靠近最小值的方向；
• 不一定收敛，有可能在最小值的附近很小的范围内波动；
• 如果在最小值附近波动，可以慢慢减小学习率 α α 。
  
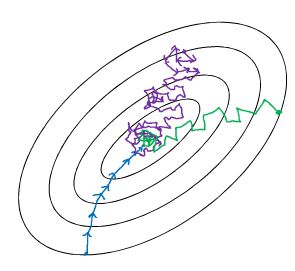
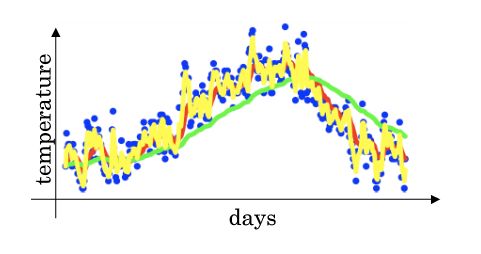
  蓝色为batch梯度下降；
  紫色为随机梯度下降；
  绿色为mini batch梯度下降。

选择mini batch size 的指导原则

• 如果训练集小（m <= 2000）：用batch梯度下降；
• 其他选择mini batch梯度下降；
• 典型的mini batch size(64-512之间)：64、128、256、512（选择2的次幂，代码会运行的快一些）；
• 确保mini batch符合CPU/GPU的内存；
• 需要对mini batch size选择一些不同的值来挑选使得模型的代价函数下降最快的一个。

2.3 指数加权平均

接下来几节学习比梯度下降快的优化算法。
在学习这些算法前，必须学会指数加权平均（统计学叫指数加权移动平均）。

• 指数加权平均：
  
  V0=0 V 0 = 0
  
  
  Vt=βVt−1+(1−β)θt V t = β V t − 1 + ( 1 − β ) θ t
  
  其中， Vt V t 近似为 11−β 1 1 − β 天的数据平均值； 0<=β<=1 0 <= β <= 1 ；
  
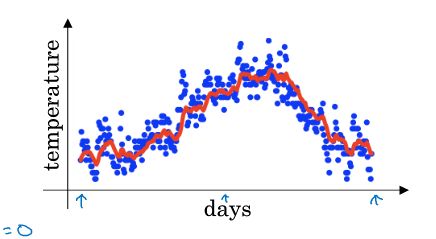
  β β 越大，曲线越平滑，但曲线会进一步右移；
  β β 越小，曲线波动越大，更有可能出现异常值，但能更好的适应数据的变化趋势 。
  
  指数加权平均可以理解为：由过去几天的数据在今天的平均值构成的曲线。

2.4 理解指数加权平均

向量化 Vθ V θ 的计算，基本上只占一行代码。
Vθ=0 V θ = 0
repeat：{ r e p e a t ： {
    get next θt         g e t   n e x t   θ t
    Vθ=βVθ+(1−β)θt         V θ = β V θ + ( 1 − β ) θ t
} }

优点：

• 代码量少；占用极小内存；运算量小；结果虽不精确但也不赖。
  
  • 不是最好的计算平均数的方法，也不是最精确的。 但如果使用一个窗去计算10天的平均数，会有很多行代码，执行更加复杂，计算成本更加高昂。

2.5 指数加权平均的偏差修正

如果没有偏差修正，曲线的最左侧很小，无法反应真实情况。
那么添加偏差修正会改善这种情况。
即：     Vθ=βVθ+(1−β)θt1−βt         V θ = β V θ + ( 1 − β ) θ t 1 − β t
分开写：
Vθ=0 V θ = 0
repeat：{ r e p e a t ： {
    get next θt         g e t   n e x t   θ t
    Vθ=βVθ+(1−β)θt         V θ = β V θ + ( 1 − β ) θ t
    Vθ=Vθ/(1−βt)         V θ = V θ / ( 1 − β t )
} }
对结果除以 1−βt 1 − β t ，效果是能够消除一开始的偏差，而对后期没有影响。
大部分人不愿意使用偏差修正，而是熬过初始时期。
如果你关心初始时期的偏差， 偏差修正能够帮助你在模型训练的早期获得更好的估计。

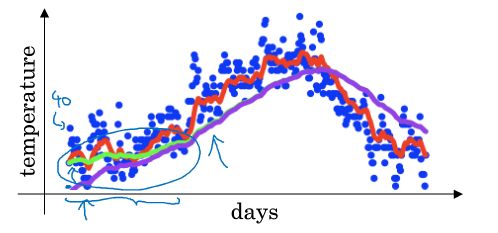
紫色为没有偏差修正，绿色为偏差修正后。

2.6 动量梯度下降法Gradient descent with momentum

训练速度比标准的梯度下降法要快。

• 基本思想：
  计算梯度的指数加权平均数，作为新的梯度，来训练网络。
        

标准梯度下降的缺点：

标准梯度下降（包括batch梯度下降、mini batch梯度下降、随机梯度下降），下降过程中存在波动。导致：1，训练模型耗时；2，无法使用过大的学习率 α α 。为了避免摆动过大，需要使用较小的 α α 。
在纵轴上，希望学习的慢一点；在横轴上，希望学习快。

momentum 梯度下降：

Vdw=0、Vdb=0 V d w = 0 、 V d b = 0
On iteration t： O n   i t e r a t i o n   t ：
    compute dw、db on current mini-batch         compute dw、db on current mini-batch
    Vdw=βVdw+(1−β)dw         V d w = β V d w + ( 1 − β ) d w
    Vdb=βVdb+(1−β)db         V d b = β V d b + ( 1 − β ) d b
    w=w−αVdw         w = w − α V d w
    b=b−αVdb         b = b − α V d b
两个超参数：

• α α 学习速率；
• β β 控制着指数加权移动平均数，一般为 β=0.9 β = 0.9 (具有鲁棒性)；

一般不会添加偏差修正；

在竖直方向上，计算指数加权移动平均值，正负相抵，减少纵轴方向上的波动；
在水平方向上，所有的微分都是指向最小值方向的，所以指数加权移动平均值的影响不大；
所以，纵轴方向波动减小，横轴方向运动更快。
即，在抵达最小值的路上减少了摆动。

想象一个碗装的函数，开口朝上。一个点位于碗的上沿。momentum梯度下降就相当于给下降的小球一个加速度。因为 β β 比1小一些，类似于摩擦力，所以速度不会无限制的增大下去。

在 Vdw=βVdw+(1−β)dw V d w = β V d w + ( 1 − β ) d w 中， Vdw V d w 就是前一刻的速度， dw d w 就是加速度。小球具有的动量会越来越大。

与梯度下降每次迭代都是独立的不同，模型可以从momentum梯度下降中获得一个越来越大的动量。而这个动量是跟以前的若干次梯度下降有关系的。

图像来自深度学习优化函数详解（4）– momentum 动量法

momentum GD可以想象成小球从坡上往下滚。小球的动量越来越大，过最低点后仍然会往前冲，如果冲到了另一个下坡。，有可能到一个更低点（更好的局部极小值）。如果动量没那么大，会慢慢的慢下来，再次返回到第一个低点。

2.7 RMSprop

• RMSprop：root mean square propagation，方均根传播
• 作用：加速梯度下降
• 简化的算法说明：
  On iteration t: On iteration t:
      compute dw, db on current mini-batch         compute dw, db on current mini-batch
       Sdw=β2Sdw+(1−β2)(dw)2           S d w = β 2 S d w + ( 1 − β 2 ) ( d w ) 2
       Sdb=β2Sdb+(1−β2)(db)2           S d b = β 2 S d b + ( 1 − β 2 ) ( d b ) 2
       w=w−αdwSdw√           w = w − α d w S d w
       b=b−αdbSdb√           b = b − α d b S d b
  
• 现在假设b的方向为纵向，w的方向为横向，那么蓝色线为梯度下降的路线。
  而RMSprop因为 S S 的存在:
  一开始前进方向的 dw d w 小，垂直方向的 db d b 大，梯度小反而由于 Sdw−−−√ S d w 做分母，导致 w w 变化大， b b 变化小，所以将垂直方向压缩，水平方向拉伸，导致波动减小，这样加快训练速度。
  同时，由于波动减小（不容易发生学习速率过大时导致不收敛或发散的问题），我们可以设置更大的学习速率 α α 。
• 实际上前进方向和垂直于前进方向的方向（纵轴方向）上的参数不一定就是 w w 、 b b 。有可能是如图：
  
  • 
    纵轴为 w1、w3、w7 w 1 、 w 3 、 w 7 、横轴为 w2、w4....... w 2 、 w 4 . . . . . . .
• 为什么叫做RMSprop？
  
  •      Sdw=β2Sdw+(1−β2)(dw)2           S d w = β 2 S d w + ( 1 − β 2 ) ( d w ) 2 的 (dw)2 ( d w ) 2 是平方和；
  •      w=w−αdwSdw√           w = w − α d w S d w 的 Sdw−−−√ S d w 是平方根；
• 超参数叫做 β2 β 2 是为了和momentum算法的超参数 β β 区分开来，因为有两个算法的结合算法；
• 为防止 Sdw−−−√ S d w 出现的接近于0的情况(导致参数变动很大)，一般在 w=w−αdwSdw√ w = w − α d w S d w 添加一个很小的数字 ϵ ϵ （ ϵ=10−8 ϵ = 10 − 8 ），防止这种情况的发生，即：
  
       w=w−αdwSdw−−−√+ϵ           w = w − α d w S d w + ϵ

2.8 Adam 优化算法

• Adam：Adaptive Moment Estimation（自适应矩估计）
• 将momentum和RMSprop结合起来，得到速度更快的优化算法：Adam优化算法；
• 算法伪代码：
  Vdw、Vdb、Sdw、Sdb=0 V d w 、 V d b 、 S d w 、 S d b = 0
  On iteration t: On iteration t:
      Vdw=β1Vdw+(1−β1)dw、    Vdb=β1Vdb+(1−β1)db     <−−−(momentum)         V d w = β 1 V d w + ( 1 − β 1 ) d w 、         V d b = β 1 V d b + ( 1 − β 1 ) d b           < − − − ( m o m e n t u m )
      Sdw=β2Sdw+(1−β2)(dw)2、Sdw=β2Sdw+(1−β2)(dw)2     <−−−(RMSprop)         S d w = β 2 S d w + ( 1 − β 2 ) ( d w ) 2 、 S d w = β 2 S d w + ( 1 − β 2 ) ( d w ) 2           < − − − ( R M S p r o p )
       Vcorrecteddw=Vdw / (1−βt1)、Vcorrecteddb=Vdb / (1−βt1)           V d w c o r r e c t e d = V d w   /   ( 1 − β 1 t ) 、 V d b c o r r e c t e d = V d b   /   ( 1 − β 1 t )
       Scorrecteddw=Sdw / (1−βt2)、Scorrecteddb=Sdb / (1−βt2)           S d w c o r r e c t e d = S d w   /   ( 1 − β 2 t ) 、 S d b c o r r e c t e d = S d b   /   ( 1 − β 2 t )
        w=w−α(VcorrecteddwScorrecteddw√+ϵ)             w = w − α ( V d w c o r r e c t e d S d w c o r r e c t e d + ϵ )
        b=b−α(VcorrecteddbScorrecteddb√+ϵ)             b = b − α ( V d b c o r r e c t e d S d b c o r r e c t e d + ϵ )
• 超参数：
  
  • α α ：学习速率
    
    • 调试，找到较好的值；
  • β1 β 1 ： dw d w 的移动加权平均值
    
    • 0.9（一般情况下）；
  • β2 β 2 ： dw2 d w 2 的移动加权平均值
    
    • 0.999（Adam算法作者推荐）;
  • ϵ ϵ ：不太重要，不会影响算法的表现
    
    • 10−8 10 − 8 （Adam算法作者推荐）;
  • 一般情况下，人们使用 β1 β 1 、 β2 β 2 、 ϵ ϵ 的缺省值，不断尝试不同的 α α 值，寻求比较好的结果。
• momentum、RMSprop、Adam是经受住考验的，适用于不同深度学习结构的优化算法；
• Adam：Adaptive Moment Estimation（自适应矩估计）叫自适应矩估计的原因：
  
  • Vdw V d w 是 dw d w ( db d b )的估计，即对梯度的一阶矩估计，叫做第一矩；
  • Sdw S d w 是 dw2 d w 2 ( db2 d b 2 )的估计，即对梯度的二阶矩估计，叫做第二矩；
  • 第一矩和第二矩根据梯度的变化进行动态调整；
  • α α 后边的部分对 α α 形成动态约束，而且有明确的范围；
• 优点：
  
  • 对内存需求小；
  • 为不同的参数计算不同的自适应学习率；
  • 适用于大多数非凸优化；
  • 适用于大数据集和高维空间；

2.9 学习率衰减

为什么要计算学习率衰减？

以固定的学习率 α α 去学习，在mini batch过程中存在噪声，下降的过程如上图所示，不会精确的收敛到最优解，而是在附近大幅度地振荡。

如果学习率会衰减，在学习初期的时候， α α 比较大，学习的速率比较快，随着 α α 的减小，步伐也渐渐变慢变小。最后学习曲线在最小值附近的一小块区域内摆动。

使用学习率衰减的原因是：
学习初期可以承受较大的步伐。
到了收敛的阶段，小的学习率可以让步伐变得小一些。

如何进行学习率衰减?

1 epoch = 1 pass through data，即遍历一遍数据集；

第一次遍历数据集，（将数据集分为若干mini batch），为epoch 1；
第二次，为epoch 2；
那么：

α=11+decayRate∗epochNumα0 α = 1 1 + d e c a y R a t e ∗ e p o c h N u m α 0

学习率衰减的图像大致如下;

α0=0.2 α 0 = 0.2	decay rate = 1
epoch	α α
1	0.1
2	0.067
3	0.05
4	0.04
。。。	。。。

• 超参数：
  
  • α α
  • decay rate d e c a y   r a t e
    为了达到比较好的效果，必须尝试不同的值，包括： α α 、 decay rate d e c a y   r a t e

其他学习率衰减的办法

• 指数衰减：
  
  α=0.95epachNum∗α0 α = 0.95 e p a c h N u m ∗ α 0
  
  其中，0.95指代一个比1小的数字；
• 离散下降：
  
• 其他方法：
  
  其中，k为常数，t为mini batch的次数；
• 手动衰减

学习速率衰减可以加快训练的速度；
但在一开始调整模型的超参数的时候，不考虑学习率衰减；
设置一个固定的学习速率，待尝试出一个比较好的模型后，可以用学习速率衰减加快训练。

2.10 局部最优的问题

鞍点

我们提起局部最优，往往想到的是如下图所示：

但梯度为0的点（驻点）不一定是一个局部极小值点，也有可能是鞍点。
往往代价函数梯度为0的点，是鞍点。


尽管梯度为0，但是在一个方向上为极小值点，在另一个方向上为极大值点。

平稳段问题

在碰到鞍点这种情况的时候，鞍点附近为平稳段；
在平稳段，由于梯度接近于0，所以学习的步伐很小；
如图，算法慢慢抵达平稳段的鞍点，然后慢慢走出平稳段，这需要花费很长时间。

在训练较大的神经网络时：

• 不太可能会陷入一个不太好的局部最优解中（因为参数多，被定义在高纬度空间中，那里充满了鞍点）；
• 平稳段会使得学习速率变慢（各种优化算法的用武之地，例如Adam，用来加快训练速度，尽快走出平稳段）；

第三周 超参数调试、Batch Normalization和程序框架

3.1 超参数调整

超参数重要程度分级

α α 最重要；
其次是黄色部分；
最后是紫色部分；

随机

• 随机尝试超参数，而不是用网格选择超参数；
  
  • 因为并不能提前知道哪一个超参数更重要；比如，选择的两个超参数是 α α 和 ϵ ϵ ，如下图所示，那么网格法在尝试25组数据后，实际上 α α 只尝试了5种数据；而随机选择的话， α α 可以尝试25种数据；所以第二种可能下更有可能找到效果最好的那个。
    
    往往一个模型的超参数不止两个，在多个超参数的情况下，我们事先不知道哪个超参数更重要的时候，使用随机的选择超参数的组合，能够探究更多的重要超参数的潜在值。
• 策略：由粗到细
  
  • 在整个超参数构成的空间随机选取一些点尝试后，发现某些区域能取得更好的成果，那么在该区域进行精细的搜索；

随机取值可以提高对超参数的搜索效率。

3.2 为超参数选择合适的范围

给 α α 取值

使用对数尺度。
在Python中的用法：

也就是，如果 α α 的范围在 10a 10 a 到 10b 10 b 之间，那么，r的范围为[a, b]。
在[a, b]的范围内对r进行随机均匀取值。

即， α α 取值在对数刻度上随机均匀取值；希望能在每十倍程里边探索的 α α 的值一样多。

给 β β 取值（给有指数加权平均值的超参数取值）

1−β=10r 1 − β = 10 r
β=1−10r β = 1 − 10 r

即 β β 在0.9-0.99、0.99-0.999之间探索的值一样多。

• 为什么不用线性轴取值？
  当 β β 接近于1时，所得结果的灵敏度会发生变化，即使 β β 有微小的变化。
  
  需要更加密集的在 β β 接近于1的区间内取值。这样才能更有效的分布取样点。
  在超参数的选择中，对超参数的标尺做出正确的选择，可以提高效率。
  如果标尺总是选择线性标尺，可能就需要取更多的采样点。

3.3 超参数调整的实践：Pandas VS Caviar

随着算法的不断改进、数据的不断变化，运算硬件的升级等，每隔几个月至少一次去重新测试和评估超参数。

超参数调整的两种不同方式(取决于算力大小)：

• 照看一个模型（babysitting one model）:
  
  • 情景：具有庞大的数据集但算力不够，只可以负担起试验一个模型or一小批模型；
  • 做法：随着时间的推移，不断地观察模型的表现，调整其超参数；（之所以这么做，是因为不能在同一时间内试验大量模型）
  • 熊猫模式：一胎只生一个，全力照看这一个宝宝。
• 同时训练多个模型（training many models in parallel）:
  
  • 情景：算力足够；
  • 做法：多个模型同时训练，每个模型的超参数不同，观察其表现，择优录取；
  • 鱼子模式：鱼每次产卵一亿个，但不会多照料其中的某一个鱼子，一视同仁。只是希望这一堆鱼子里边，能有一个或者一部分表现出色，变成鱼宝宝。

3.4 batch normalization(归一化网络的激活函数)

优点：

• 使超参数搜索变容易；
• 使NN对超参数的选择更加稳定；
• 超参数的范围更庞大；
• 超参数的效果更好；
• 很容易训练网络甚至是深层网络；

normalizing inputs to speed up learning

对于逻辑回归，归一化输入，可以加速训练 w、b w 、 b 。
X(i) 2 X ( i )   2 即 X X 中的每一个元素的平方，即点积。

那么，对于深层网络，可不可以归一化每层网络的激活函数的输出值 a[l] a [ l ] ，来加速训练 w[l+1]、b[l+1] w [ l + 1 ] 、 b [ l + 1 ] ？

严格来说，我们归一化的是 z[l] z [ l ] ，而不是 a[l] a [ l ] 。
学术界对归一化 z[l] z [ l ] 还是 a[l] a [ l ] 有争论。
但此处，我们学习归一化 z[l] z [ l ] 。
batch norm就是将归一化过程从输入层推广到了隐藏层。使得隐藏层单元值的均值和方差标准化，或者取得想要的均值和方差。

实现Batch Norm

Given some intermediate values in NN :z[l](1)、...、z[l](m) Given some intermediate values in NN : z [ l ] ( 1 ) 、 . . . 、 z [ l ] ( m )
μ=1m∑iz[l](i) μ = 1 m ∑ i z [ l ] ( i )
σ2=1m∑i(z[l](i)−μ)2 σ 2 = 1 m ∑ i ( z [ l ] ( i ) − μ ) 2
z[l](i)norm=z[l](1)−μσ2+ϵ√ z n o r m [ l ] ( i ) = z [ l ] ( 1 ) − μ σ 2 + ϵ
z˜[l](i)=γz[l](i)norm+β z ~ [ l ] ( i ) = γ z n o r m [ l ] ( i ) + β
usez˜[l](i) instend of z[l](i) use z ~ [ l ] ( i )  instend of  z [ l ] ( i )
其中， γ、β γ 、 β 为模型的learnable parameters。

参数 γ、β γ 、 β 的意义在于，给出任意均值和方差的 z z 。
比如，如果隐藏层使用的是sigmoid激活函数，那么，我们需要的输入可能就不是均值为0，方差为1的输入数据。

• β β 不是momentum、adam、rms prop算法中的超参数，此处仅为BN的参数。

3.5 将 Batch Norm加入到神经网络

BN加入到神经网络

在反向传播更新 β、γ β 、 γ 的时候，可以使用梯度下降，也可以使用其他优化算法。
在深度学习框架中，不用自己去实现BN。已经有了现成的框架可以实现。
比如在tensorflow中，使用：tf.nn.batch_normalization()
虽然不用实现细节，但是必须了解原理。

BN working with mini-batches

实践中，BN往往和训练集的mini-batch一起使用。

• 第一批数据进入NN；
  
• 反向传播，更新网络参数 w[l]、β[l]、γ[l] w [ l ] 、 β [ l ] 、 γ [ l ] （没有 b[l] b [ l ] ）;
• 第二批数据进入NN（使用上次的NN参数）；
  
• 反向传播，更新网络参数 w[l]、β[l]、γ[l] w [ l ] 、 β [ l ] 、 γ [ l ] （没有 b[l] b [ l ] ）;
• 第三批数据进入NN（使用上次的NN参数）；
  
  直到收敛。

网络的参数为： w[l]、β[l]、γ[l] w [ l ] 、 β [ l ] 、 γ [ l ] 。

• 为什么没有 b[l] b [ l ] ？
  因为BN的过程，先是把数据的均值转换成0。再利用训练出来的参数 β β 给数据新的均值。那么，原始数据的参数 b[l] b [ l ] 不管如何取值，都会在均值转换成0这一步消掉。也就是，有没有 b[l] b [ l ] ，都不会影响到最后的 Z~[i] Z ~ [ i ] 。
  

• 如果输入数据 X{t} X { t } (第t批数据)为(n,m)，那么，

  • Z[1] Z [ 1 ] 为 (n[1]、m) ( n [ 1 ] 、 m ) —–> Z[l] Z [ l ] 为 (n[l]、m) ( n [ l ] 、 m ) ；
  • w[l] w [ l ] 为 (n[l]、n[l−1]) ( n [ l ] 、 n [ l − 1 ] ) ；
  • β[l] β [ l ] 和 γ[l] γ [ l ] 为 (n[l]、1) ( n [ l ] 、 1 ) (Python的广播机制)；
    
    图中 Z[l] Z [ l ] 为 (n[l]、1) ( n [ l ] 、 1 ) 的原因是输入的数据个数为1。

实现带BN的梯度下降：

for t = 1 ...... num of mini_batches： for t = 1 ...... num of mini_batches ：
     compute forward prop on X{t}：           compute forward prop on  X { t } ：
          in each hidden layer, use BN to replace Z[l]  with  Z~[l]；                     in each hidden layer, use BN to replace  Z [ l ]     w i t h     Z ~ [ l ] ；
     use back prop to compute dw[l]、dβ[l]、dγ[l]；           use back prop to compute  d w [ l ] 、 d β [ l ] 、 d γ [ l ] ；
     update parameters w[l]=w[l]−αdw[l]、β[l]=β[l]−αdβ[l]、γ[l]=γ[l]−αdγ[l]；           update parameters  w [ l ] = w [ l ] − α d w [ l ] 、 β [ l ] = β [ l ] − α d β [ l ] 、 γ [ l ] = γ [ l ] − α d γ [ l ] ；

• 参数更新这一步，可以使用各种优化算法。

3.6 Batch Norm 为什么奏效？

感性的理解，貌似BN是将输入数据归一化这一技巧用到了所有的隐藏层，而输入数据归一化的好处就是能加速网络的训练，但是其实，BN之所以有效，还有更深层次的原因：

• 1.数据归一化的好处；
  
  • 代价函数变得更加圆，梯度下降的波动减小，加速训练；
  • 波动减小，可以选择更大的学习速率 α α ;
• 2.减弱covariate shift 问题；
• 3.轻微的正则化效果；

covariate shift 问题：

对这个逻辑回归模型
用一个数据集训练网络来找猫。训练集正例的猫都是黑色的。而真正的数据集的正例是各种颜色的猫。
即训练集和验证集（以及测试集）的数据分布不一样。

那么，在左边训练的很好的模型，不能期待它同样在右边也运行的很好。即使真的存在在左右两侧都运行的很好的一个函数。

但你不能期望自己有这么好的运气。
这种问题，就叫做covariate shift 。

• covariate shift 问题 ：
  
  • 在这个单层的网络或者逻辑回归模型中，训练集和验证集（以及测试集）的数据分布不一致。在训练集上训练出来的模型无法在验证集（以及测试集）上取得良好的效果。我们把训练集和验证集（以及测试集）的数据样本分布不一致的问题叫做covariate shift （协方差漂移）[非正确概念]
    

上边这个概念其实是有些错误的，再加以延伸：

上图有一个深层的网络，如果我们单看中间的第三层，在该层之前的前一层的输出 a[2]1 a 1 [ 2 ] 、…、 a[2]4 a 4 [ 2 ] 作为它的输入。
那么，蓝色部分的参数 w[l] w [ l ] 、 b[l] b [ l ] 由于参数更新而发生了变化，在发生变化后的网络中输入数据，最后得到的新的 a[2]1 a 1 [ 2 ] 、…、 a[2]4 a 4 [ 2 ] 可能和参数更新前的分布不一致。
或者说，在参数 w[l] w [ l ] 、 b[l] b [ l ] 更新前后，算出来的 a[2]1 a 1 [ 2 ] 、…、 a[2]4 a 4 [ 2 ] 的分布可能不一致（方差不同，均值不同）。
不同分布的 a[2]1 a 1 [ 2 ] 、…、 a[2]4 a 4 [ 2 ] 在输入后半部分以后，必然引起不同的结果。
这就是covariate shift 问题。

• 为什么covariate shift 问题对神经网络来说是个问题？
  
  • 对每一层而言，参数更新后，该层的输入分布就有可能发生变化。层层叠加后，输入分布变化的非常大，后边的隐层需要不断地去重新适应这些变化。神经网络没有一个坚实的基础来训练数据。训练一个网络的难度大。

减弱covariate shift

• 也就是说，由于BN的存在，从某一个隐层看过来，前边的神经网络部分给该隐层的输入虽然会不断的发生变化（因为前边的神经网络的参数在不断的更新），但是，对该隐层而言，输入值的分布（均值、方差）保持不变。这个均值和方差要么是0和1，要么是由 γ γ 和 β β 决定。
• BN限制了前层参数更新对数值分布影响的程度。
• BN减少了输入值（对每一层而言）分布改变的问题。使得这些值变得稳定。即使这些值的分布发生变化，也是较小的变化。
• BN减弱了前层参数和后层参数的作用之间的联系。使得每一层都可以自己学习，稍稍独立于其他层。有助于加速整个网络的学习。

BN的轻微正则化

每一次计算均值和方差都是在一个mini batch上进行，而不是整个数据集。这样计算出来的 z~[l] z ~ [ l ] 会有噪声。所以，会对每一个隐藏层的激活函数添加噪声进去。这迫使后层的单元不过分依赖任何一个隐藏单元。类似于dropout，这种由在mini batch上计算均值和误差的方式会加入噪声，从而达到轻微的正则化效果。
算是BN的一个副作用。有时候，会期望这种副作用，有时候又要避免。
这种轻微正则化会随着mini batch的size的增大而减小。比如，mini batch为128的数据集，就比为512的数据集的正则化作用明显。

在训练集上，BN一次只能处理一个mini batch的数据。在一个mini batch上计算均值和方差。
而验证集和测试集不会去分mini batch。这时候BN怎么work呢？

3.7 测试时的 Batch Norm

测试的时候，没有mini batch，而测试集数据又是一个一个喂给模型的，没有 μ μ 和 σ2 σ 2 ，这个时候， μ μ 和 σ2 σ 2 从哪里来？
容易想到的是，用整个训练集数据去计算一个 μ μ 和 σ2 σ 2 ；
但更好的办法是，使用训练集数据在mini batch过程中计算出来的 μ μ 和 σ2 σ 2 的移动加权平均值。

3.8 Softmax 回归

关键词：softmax层，softmax激活函数
从二分类到多分类，从logistic回归推广到softmax回归。
注意：

• 如果是只有输入层到输出层，没有隐藏层，那么这是softmax回归。
• 如果是在一个具有隐藏层的神经网络最后加入了一层，该层使用softmax激活函数，那么这是给神经网络加入softmax层。
  
  现在是一个四分类的问题，输出层为4个值，要将其变成概率。
  加入一个Softmax层，其激活函数为 a[L]=g[L](Z[L]) a [ L ] = g [ L ] ( Z [ L ] ) ：
  
  • t=e(Z[L]) t = e ( Z [ L ] )
  • a[L]=t∑4jtj a [ L ] = t ∑ j 4 t j ，那么， a[L]i=ti∑4jtj a i [ L ] = t i ∑ j 4 t j
    或者写成：
    
    a[L]=e(Z[L])∑4je(Z[L])j a [ L ] = e ( Z [ L ] ) ∑ j 4 e ( Z [ L ] ) j
    
    softmax激活函数和其他激活函数不同，
• 其他激活函数的输入输出都是数值，softmax激活函数输入输出都是向量。
  
  
  上图是使用没有隐藏层的一个神经网络，即输入层，输出层，然后经过softmax层。就是logistic回归的一般形式。因为没有引入隐藏层，整个决策边界都是线性决策边界。

以上为给一个多分类的神经网络加入softmax层，让其输出变成概率值。

在没有加入隐藏层的情况下，有logistics回归以及其升级版的softmax回归。
学习吴恩达ufldl的softmax回归

3.9 训练一个 Softmax 分类器

hard vs soft

---

softmax是相对于hardmax的一个说法；
对一个向量：

所谓hardmax：

即在对应原向量最大元素的位置上放置1，其他位置为0；

所谓softmax：

成了概率值，这四个元素之和为1；
最大概率值对应的就是原始向量的最大值；

相对于hard max，soft max所做的从向量  z    z   到最终概率的映射更为温和；

理解softmax回归

softmax回归是将logistics回归从二分类问题推广到了多分类问题：

• 如果使用softmax来解决二分类问题，那么这就等同于一个logistics回归模型；而且是一个冗余的logistics回归模型；其代价函数、假设函数都一致。但此时，logistics regression的输出层只需要一个单元，而softmax需要两个单元。产生了冗余。

多个类别的分类问题；

• 如果这些类别之间互斥，用softmax regression；
• 如果类别之间不是互斥的，用多个logistics regression；

损失函数loss function

也就是，要让损失函数 L(y^,y) L ( y ^ , y ) 最小，在上图中，就必须让正确的标签值 y2 y 2 所对应的预测概率 y^2 y ^ 2 尽可能的大。

代价函数cost function

3.10 深度学习框架