大二下:概率论与数理统计复习 2.随机变量及其分布之习题加练
大二下:概率论与数理统计复习 导航页:https://blog.csdn.net/COCO56/article/details/100152856
文章目录
- 1. 已知随机变量X的概率密度求$f_Y(y)$
- 2.
- 3.
- 4. 已知随机变量X的概率密度求$f_Y(y)$
1. 已知随机变量X的概率密度求 f Y ( y ) f_Y(y) fY(y)
已 知 随 机 变 量 X 的 概 率 密 度 函 数 f X ( x ) = { 1 5 e − x 5 x > 0 0 , x ≤ 0 已知随机变量X的概率密度函数\LARGE f_X(x)=\left\{\begin{aligned}&\frac{1}{5}e^{-\frac{x}{5}}&x>0\\&0,&x\le0\end{aligned}\right. 已知随机变量X的概率密度函数fX(x)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧51e−5x0,x>0x≤0 , 则 Y = 2 X + 1 的 密 度 函 数 f Y ( y ) = { 1 10 e − y − 1 10 , y > 1 0 , y ≤ 1 ‾ . ,则Y=2X+1的密度函数f_Y(y)=\underline{\LARGE\left\{\begin{aligned}&\frac{1}{10}e^{-\frac{y-1}{10}},&y>1\\&0,&y\le1\end{aligned}\right. }. ,则Y=2X+1的密度函数fY(y)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧101e−10y−1,0,y>1y≤1.
解 : 解: 解:
∵ F Y ( y ) = P ( Y ≤ y ) = P ( 2 X + 1 ≤ y ) = P ( X ≤ y − 1 2 ) = F X ( y − 1 2 ) \because F_Y(y)=P(Y\le y)=P(2X+1\le y)=P(X\le\frac{y-1}{2})=F_X(\frac{y-1}{2}) ∵FY(y)=P(Y≤y)=P(2X+1≤y)=P(X≤2y−1)=FX(2y−1)
∴ f Y ( y ) = f X ( y − 1 2 ) × ( y − 1 2 ) ′ = 1 2 f X ( y − 1 2 ) \therefore f_Y(y)=f_X(\frac{y-1}{2})\times(\frac{y-1}{2})'=\frac{1}{2}f_X(\frac{y-1}{2}) ∴fY(y)=fX(2y−1)×(2y−1)′=21fX(2y−1)
= { 1 2 × 1 5 e − y − 1 2 5 , y − 1 2 > 0 0 , y − 1 2 ≤ 0 \qquad\ \ \ \ \ \LARGE =\left\{\begin{aligned}&\frac{1}{2}\times\frac{1}{5}e^{-\frac{\frac{y-1}{2}}{5}},&\frac{y-1}{2}>0\\&0,&\frac{y-1}{2}\le0\end{aligned}\right. =⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧21×51e−52y−1,0,2y−1>02y−1≤0
= { 1 10 e − y − 1 10 , y > 1 0 , y ≤ 1 \qquad\ \ \ \ \ \LARGE =\left\{\begin{aligned}&\frac{1}{10}e^{-\frac{y-1}{10}},&y>1\\&0,&y\le1\end{aligned}\right. =⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧101e−10y−1,0,y>1y≤1
2.
设 X 在 ( − π 2 , π 2 ) 服 从 均 匀 分 布 , 求 Y = cos X 的 分 布 函 数 。 设X在(-\frac{\pi}{2},\frac{\pi}{2})服从均匀分布,求Y=\cos X的分布函数。 设X在(−2π,2π)服从均匀分布,求Y=cosX的分布函数。
解 : 解: 解:
X ∼ f X ( x ) = { 1 π , − π 2 < x < π 2 0 , 其 他 X\sim f_X(x)=\left\{\begin{aligned} &\frac1\pi, &-\frac{\pi}{2}
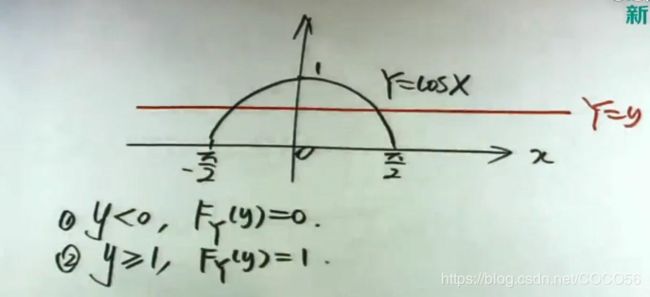
则 F Y ( y ) = P { Y ≤ y } = P { cos X ≤ y } 则F_Y(y)=P\{Y\le y\}=P\{\cos X\le y\} 则FY(y)=P{Y≤y}=P{cosX≤y}
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休。”
1 : y < − 1 , F Y ( y ) = 0 1:y<-1,F_Y(y)=0 1:y<−1,FY(y)=0
2 : y ≥ 1 , F Y ( y ) = 1 2:y\ge1,F_Y(y)=1 2:y≥1,FY(y)=1
3 : 1 ≤ y < 1 , F Y ( y ) = P { Y ≤ y } = P { cos X ≤ y } 3:1\le y<1, F_Y(y)=P\{Y\le y\}=P\{\cos X\le y\} 3:1≤y<1,FY(y)=P{Y≤y}=P{cosX≤y}
= P { 0 < X < π } \qquad\qquad\qquad\qquad\quad=P\{0
= ∫ 0 π 1 π d x \qquad\qquad\qquad\qquad\quad=\int_{0}^{\pi}\frac{1}{\pi}dx =∫0ππ1dx


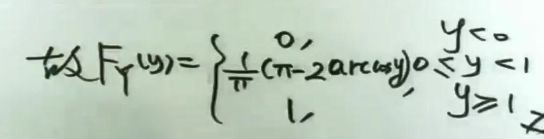
3.
4. 已知随机变量X的概率密度求 f Y ( y ) f_Y(y) fY(y)
设 随 机 变 量 X ∼ U ( 0 , π ) , 试 求 随 机 变 量 Y = sin X 的 概 率 密 度 函 数 . 设随机变量X\sim U(0,\pi),试求随机变量Y=\sin X的概率密度函数. 设随机变量X∼U(0,π),试求随机变量Y=sinX的概率密度函数.
解 : 解: 解:
由 均 匀 分 布 U ( a , b ) 的 概 率 密 度 函 数 f ( x ) = { 1 b − a , a < x < b 0 , 其 他 , 由均匀分布U(a,b)的概率密度函数f(x)=\left\{\begin{aligned} &\frac{1}{b-a}, &a
得 U ( 0 , π ) 的 概 率 密 度 函 数 为 f ( x ) = { 1 π , 0 < x < π 0 , 其 他 得U(0,\pi)的概率密度函数为f(x)=\left\{\begin{aligned} &\frac1\pi, &0
∵ F Y ( y ) = P { Y ≤ y } = P { sin X ≤ y } = P { X ≤ arcsin y } = F X ( arcsin y ) \because F_Y(y)=P\{Y\le y\}=P\{\sin X\le y\}=P\{X\le\arcsin y\}=F_X(\arcsin y) ∵FY(y)=P{Y≤y}=P{sinX≤y}=P{X≤arcsiny}=FX(arcsiny)
∴ f Y ( y ) = f X ( arcsin y ) × ( arcsin y ) ′ = 1 1 − y 2 f X ( arcsin y ) \therefore \LARGE f_Y(y)=f_X(\arcsin y)\times(\arcsin y)'=\frac{1}{\sqrt{1-y^2}}f_X(\arcsin y) ∴fY(y)=fX(arcsiny)×(arcsiny)′=1−y21fX(arcsiny)
= { 1 1 − y 2 × 1 π , 0 < arcsin y < π 0 , 其 他 \qquad\qquad\quad\ \ \LARGE=\left\{\begin{aligned} &\frac{1}{\sqrt{1-y^2}}\times\frac1\pi, &0<\arcsin y<\pi\\ &0, &其他\end{aligned}\right. =⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧1−y21×π1,0,0<arcsiny<π其他
= { 1 π 1 − y 2 , 0 < y < 1 0 , 其 他 \qquad\qquad\quad\ \ \LARGE=\left\{\begin{aligned} &\frac{1}{\pi\sqrt{1-y^2}}, &0