(转载)二次剩余(知识总结+板子整理)
思路来源
https://blog.csdn.net/kele52he/article/details/78897187(二次剩余)
https://blog.csdn.net/stevensonson/article/details/85845334(二次剩余)
https://blog.csdn.net/skywalkert/article/details/52591343?locationNum=3&fps=1(Cipolla定理、二次剩余、三次剩余)
https://www.cnblogs.com/nbwzyzngyl/p/8469035.html(扩域、二次域)
https://blog.csdn.net/qq_24451605/article/details/45093911?locationNum=1(欧拉判别准则)
知识点整理
二次剩余,现在的研究范围,只在p为奇素数下进行
若存在![]() 使得
使得![]() ,则称n是模p的二次剩余
,则称n是模p的二次剩余
二次剩余的充要条件,勒让德记号余数为1
充分性:
d,x属于[1,p-1],显然与p互质;
欧拉判别准则,这里其实就是费马小定理
必要性:
用原根可以证明d,可以表示为![]() 的形式,从而得证
的形式,从而得证
二次非剩余的充要条件,勒让德记号余数为-1
不是二次剩余,则若ij=n(mod p),i和j一定不相同,
根据扩展欧几里得,
把ij%p=n,转化成 ij+pq=n,
由于gcd(i,p)=1,所以 ij+pq=1肯定有解,
因为n是1的倍数,所以ij+pq=n肯定有解
所以,j=j0+k*p,且j0≠0,故必有且只有一个解j落在[1,p-1]内
n整除p时,勒让德记号余数为0
由勒让德记号定义,显然成立
二次剩余的解n,恰有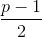 个
个
由于u和v的取值[1,p-1],所以u-v(不妨u>v)的差必在[1,p-2]之间,与素数p互质,
且u+v取值[2,2p-2],故u+v==p,说明每对和为p的值有唯一的平方值
不同对(u,v)(w,x)之间若平方相同,设v和w(w≠u)相同,
则必有u+v==p,v+w==p,w+x==p,这推得u==w,与w≠u矛盾,故平方值不同
Cipolla定理(求n给定时的一组二次剩余)
由于p是质数,所以在![]() 的展开式中,p和分母任意项互质,从而p不可被约掉,使
的展开式中,p和分母任意项互质,从而p不可被约掉,使![]() 为p的倍数
为p的倍数
x是解,那么p-x显然是解,代入![]() 即得
即得
所以,求了一个,即相当于求了另一个
扩域(类似复数域)
实际求![]() 时,由于
时,由于![]() 为非二次剩余,mod p意义下勒让德符号为-1
为非二次剩余,mod p意义下勒让德符号为-1
故可将与复数域联系,视为复数域中的i,进行复数域(a+i)的快速幂的运算,
实部单算,虚部单算,称其为扩域,只是这里![]() ,而非-1
,而非-1
由拉格朗日定理知,最终![]() 的虚部为0(不懂)
的虚部为0(不懂)
板子
#include
using namespace std;
typedef long long ll;
ll p,w;
struct field{//扩域 x实部 y虚部
ll x,y;
field(ll a=0,ll b=0){
x=a;y=b;
}
};
field operator*(field a,field b){return field(1ll*a.x*b.x%p+1ll*a.y*b.y%p*1ll*w%p,1ll*a.x*b.y%p+1ll*a.y*b.x%p);}
ll ran(){//随机数种子
static ll seed=23333;
return seed=((((((ll)seed^20030927)%p+330802)%p*9410)%p-19750115+p)%p^730903)%p;
}
ll pows(ll a,ll b){
ll base=1;
while(b){
if(b&1) base=1ll*base*a%p;
a=1ll*a*a%p;b/=2;
}
return base;
}
field powfield(field a,ll b){//扩域快速幂
field base=field(1,0);
while(b){
if(b&1) base=base*a;
a=a*a;b/=2;
}
return base;
}
ll legander(ll x){//勒让德记号
//返回-1时x不为二次剩余
//返回1时x为二次剩余
//返回0时p整除x
ll a=pows(x,(p-1)/2);
if(a+1==p) return -1;
return a;
}
ll surplus(ll x){//求b.x*b.x==x(mod p)时的b.x
//即给定x,求x为二次剩余时的解b.x
//x为非二次剩余时返回-1 while(1)期望次数两次
ll a;
if(!x)return 0;
if(legander(x)==-1) return -1;
while(1){
a=ran()%p;
w=((1ll*a*a-x)%p+p)%p;
if(legander(w)==-1) break;
}
field b=field(a,1);
b=powfield(b,(p+1)/2);
return b.x;
}
int main()
{
return 0;
}