Python金融系列第七篇:市场风险
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
第一篇:计算股票回报率,均值和方差
第二篇:简单线性回归
第三篇:随机变量和分布
第四篇:置信区间和假设检验
第五篇:多元线性回归和残差分析
第六篇:现代投资组合理论
第七篇:市场风险
第八篇:Fama-French 多因子模型
介绍
在有关金融的论文中,你可能会经常听到资产的 “beta” 或者 “市场风险” 等词。本章将解释这些术语的来源以及它们的用处。
资本资产定价模型
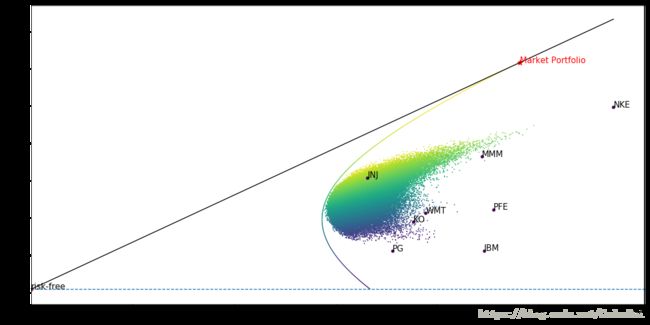
正如我们稍后将要看到的,“资产定价” 这个名称有点误导,因为 CAPM 告诉我们资产的预期收益而不是价格。在前面的内容中,我们已经介绍了以黑色线显示的资本市场线(CML):
所有投资者都应该持有 CML 的投资组合,该投资组合是通过在市场投资组合中投入我们的财富的一小部分以及在无风险资产中的剩余部分(1-w)来构建的。所以 CML 投资组合的回报是:
R = w R m a r k e t + ( 1 − w ) R 0 R = wR_{market} + (1-w)R_{0} R=wRmarket+(1−w)R0
如果,我们让 β = w \beta = w β=w ,那么上面的等式就可以变为:
R − R 0 = β ( R m a r k e t − R 0 ) R - R_{0} = \beta (R_{market} - R_{0}) R−R0=β(Rmarket−R0)
请注意, β \beta β 是衡量我们的 CML 投资组合回报对市场回报的敏感程度的指标。我们对等式两边都计算期望:
E ( R ) − R 0 = β ( E ( R m a r k e t − R 0 ) E(R) - R_{0} = \beta (E(R_{market} - R_{0}) E(R)−R0=β(E(Rmarket−R0)
我们再对两边都取协方差:
C o v ( R − R 0 , R m a r k e t ) = β C o v ( R m a r k e t − R 0 , R m a r k e t ) Cov(R-R_{0}, R_{market}) = \beta Cov(R_{market} - R_{0}, R_{market}) Cov(R−R0,Rmarket)=βCov(Rmarket−R0,Rmarket)
现在应用协方差两个基本事实:
- Cov(X+c, Y) = Cov(X, Y),其中 c 是一个常量
- Cov(X, X) = Var(X)
因此,我们可以得到 β \beta β 值为:
β = C o v ( R , R m a r k e t ) V a r ( R m a r k e t ) \beta = \frac{Cov(R, R_{market})}{Var(R_{market})} β=Var(Rmarket)Cov(R,Rmarket)
在实践中如何计算 beta
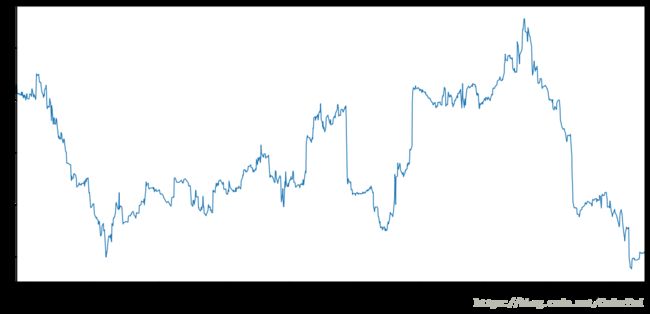
虽然资本资产定价模型很简单,但是应用中如何计算可不简单。我们首先需要选择计算回报的时间范围:我们应该使用每日,每周还是每月的回报呢?然后我们需要考虑可用于线性回归的数据点的数量。例如,如果我们使用过去1年的月度回报计算 bata 值,那么我们只有 12 个数据点太少了。此外,资产的 β \beta β 可以随着时间变化。以下图表是 GE 股票的每日数据,其中有6个月的回滚数据窗口:
GE 的 β \beta β 值约为 0.1 至 0.5 。这就是使用 β \beta β 时需要小心的原因,因为不考虑时间间隔,谈论 β \beta β 是没有意义的。
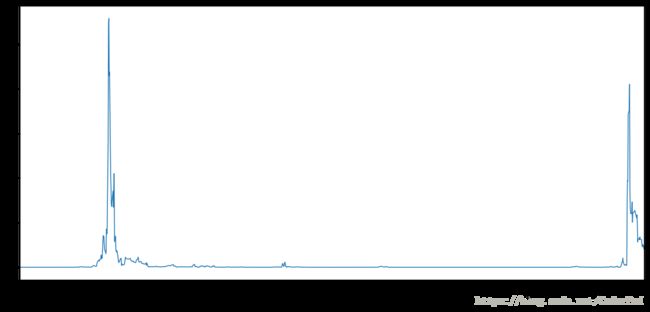
下图是 beta 的滚动 p 值。p 值在大多数时间保持接近零。然而,在一段时间内,它突然增加到接近 0.1,这就相当于 90% 的置信区间了。这可能是由于一些错误定价或者市场动荡造成的。
市场中心
如果投资组合的 β \beta β 为零,则该投资组合是市场中性的。换句话说,投资组合的回报与市场回报无关。我们说它没有“市场风险”。一些经典的市场中性策略是配对交易,beta 对冲股票投资组合和其他衍生品策略。我们从 2012 年 3月到 2015年 1 月每日都有道琼斯 30 种股票的回报。对于每只股票,其在任何特定日期的 β \beta β 均使用过去 6 个月的回报计算。随着这个 6 个月的窗口向前移动, β \beta β 当然会改变。一旦我们知道每只股票的 β \beta β 随时间的变化,我们可以问:哪些股票的 β \beta β 彼此相关?下表显示了每只股票的 β \beta β 之间的相关性。
那么我们如何构建市场中立的投资组合呢?我们来考虑两个股票 A 和 B:
R A = R 0 + β ( R m a r k e t − R 0 ) R_{A} = R_{0} + \beta (R_{market} - R_{0}) RA=R0+β(Rmarket−R0)
R B = R 0 + β ( R m a r k e t − R 0 ) R_{B} = R_{0} + \beta (R_{market} - R_{0}) RB=R0+β(Rmarket−R0)
我们将我们的资金在股票 A 上面分配 w,在股票 B 上面分配 1-w,然后市场中立意味着:
w β A + ( 1 − w ) β B = 0 ⇒ w = β B β B − β A w\beta_{A} + (1-w)\beta_{B} = 0 \space\space\space\space \Rightarrow \space\space\space\space\space w = \frac{\beta_{B}}{\beta_{B} - \beta_{A}} wβA+(1−w)βB=0 ⇒ w=βB−βAβB
如前所述, β A \beta_{A} βA 和 β B \beta_{B} βB 将随着时间而变化,因此市场中性投资组合也将变成如此。然而,只要 β A \beta_{A} βA 和 β B \beta_{B} βB 具有线性关系,我们就可以用常数 w 来实现市场中性:
β A = m β B + c \beta_{A} = m \beta_{B} + c βA=mβB+c
然后消除 β A \beta_{A} βA ,我们可以得到:
w = β B ( 1 − m ) β B − c w = \frac{\beta_{B}}{(1-m) \beta_{B} - c} w=(1−m)βB−cβB
如果 c ≈ 0 c \approx 0 c≈0 ,那么我们可以 w 为:
w = 1 1 − m w=\frac{1}{1-m} w=1−m1
注意:如果 c 很重要,那么我们需要 3 只股票来获得净值 beta,但是通常有 2 只股票足以抵消大部分市场风险。
例子
假设,我们有 PG 和 KO 两只股票,他们 6 个月滚动价格相关性为 93%。他们的 beta 之间的线性关系是:
β K O = − 0.0097 + 0.969 β P G \beta_{KO} = -0.0097+0.969 \beta_{PG} βKO=−0.0097+0.969βPG
那么市场中性的权重为:
w K O = 1 1 − 0.969 = 32.3 w_{KO} = \frac{1}{1-0.969} = 32.3 wKO=1−0.9691=32.3
w P G = 1 − w K O = − 31.3 w_{PG} = 1-w_{KO} = -31.3 wPG=1−wKO=−31.3
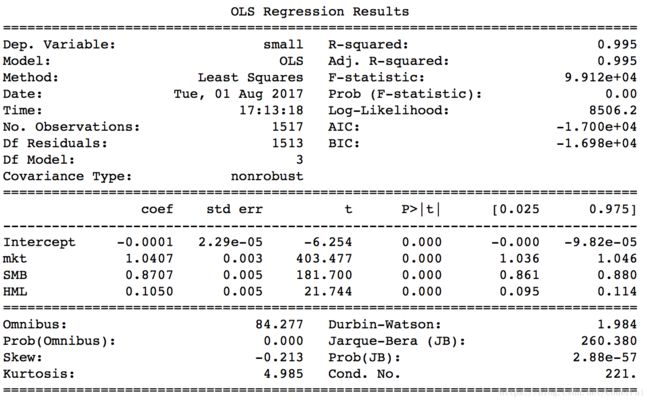
我们在样本内(2012年3月至2015年1月)和样本外测试了这个组合。它们分别达到 0.01 和 -0.004 的 beta。