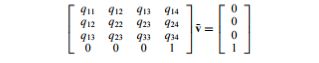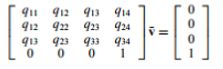实现边坍塌的网格简化方法

 一、算法介绍

关于边塌陷的网格简化方法，SIGGRAPH 有一篇97年的论文Surface Simplification Using Quadric Error Metrics（Michael&&PaulS）对这个问题进行了深入的探讨。作业里的代码就是基于这篇论文来实现的。最为核心的思想就是通过对网格图形上的每一条边通过计算一个cost来维护一个堆，每次迭代都将这个堆中cost最小的边将它移除，然后重新计算各条现有边的损失值来维护堆，直到达到给定的简化率为止。

 

首先我们来关注第一个问题：为什么我们需要网格简化？相信平时玩大型3D游戏的时候大家都会看到在越来越精美的模型中也会掺杂着一些十分粗略的模型（比如篮球游戏中的观众），其目的也很好理解，模型的复杂性直接关系到它的计算成本，过于多的计算资源都被拿来对场景中的重要的不重要的模型生成来使用，势必会影响其流畅性。因此高精度的模型在几何运算时并不是必须的，取而代之的是一个相对简化的三维模型，那么如何自动计算生成这些三维简化模型就是网格精简算法所关注的目标。

论文中最核心和部分无疑就是计算这个cost的思想，我们分两块来说明论文这部分思想：首先，每一次迭代怎么计算这个Approximating Error With Quadrics。然后我们讨论怎么初始化这个ErrorQuadrics。

                                            

     

                                            

                                           

这一部分就是paper中具体说明这个cost计算的地方。该方法在选择一条合适的边进行迭代收缩时，定义了一个描述边收缩代价的变量Δ，具体如下：对于网格中的每个顶点v，我们预先定义一个4×4的对称误差矩阵Q，那么顶点v=[vxvyvz1]T的误差为其二次项形式Δ(v)=vTQv。假设对于一条收缩边(v1,v2)，其收缩后顶点变为vbar，我们定义顶点vbar的误差矩阵Qbar为Qbar=Q1+Q2，对于如何计算顶点vbar的位置有两种策略：一种简单的策略就是在v1,v2和(v1+v2)/2中选择一个使得收缩代价Δ(vbar)最小的位置。另一种策略就是数值计算顶点vbar位置使得Δ(vbar)最小，由于Δ的表达式是一个二次项形式，因此令一阶导数为0，即，该式等价于求解：

       

其中qij为矩阵Qbar中对应的元素。如果系数矩阵可逆，那么通过求解上述方程就可以得到新顶点vbar的位置，如果系数矩阵不可逆，就通过第一种简单策略来得到新顶点vbar的位置。

      

1.对所有的初始顶点计算Q矩阵.

2.选择所有有效的边（这里取的是联通的边，也可以将距离小于一个阈值的边归为有效边）

3.对每一条有效边(v1,v2)，计算最优抽取目标v¯.误差v¯T(Q1+Q2)v¯是抽取这条边的代价（cost）

4.将所有的边按照cost的权值放到一个堆里

5.每次移除代价（cost）最小的边，并且更新包含着v1的所有有效边的代价

           

      

      

      

这一部分就是来解决另一个问题的，如何计算每个顶点的初始误差矩阵Q，在原始网格模型中，每个顶点可以认为是其周围三角片所在平面的交集，也就是这些平面的交点就是顶点位置，我们定义顶点的误差为顶点到这些平面的距离平方和：

               

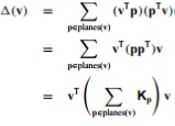
其中p=[abcd]T代表平面方程ax+by+cz+d=0(a2+b2+c2=1)的系数，Kp为二次基本误差矩阵：

               

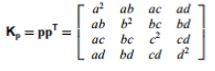
因此原始网格中顶点v的初始误差为Δ(v)=0，当边收缩后，新顶点误差为Δ(vbar)=vTbarQbarvbar，我们依次选取收缩后新顶点误差最小的边进行迭代收缩直到满足要求为止。

二、代码介绍

	void setRatio(double);//设置简化率
	void setLeftFaceNum(int);//设置最终剩余的面片数

	void input();//读入初始结果
	void start();//开始简化
	void output();//输出结果

	//点的相关操作
	Matrix calVertexDelta(int);
	MyVec3d calVertexPos(Edge&,Matrix);//根据一个边两个点的误差矩阵计算收缩后的点位置
	//边的相关操作
	void calVAndDeltaV(Edge&);//计算并确定一个边v和deltaV;	

以上几个函数就是本代码的核心函数。

首先我们来看看三个calculate函数：这三个calculate函数就是上边所说的遍历所以现在有效的边，计算如果下一条去掉的边是这一条的话，对应的代价为多少，把对应的值更新到堆里。具体来看一下，这三个函数就是一层调用下一层的关系：

MyVec3d MeshSimplify::calVertexPos(Edge& e,Matrix m){
	MyVec3d mid = (vGroup->group[e.v1].pos + vGroup->group[e.v2].pos) / 2;  //中点，应对退化情况
	m.mat[3][0] = 0;
	m.mat[3][1] = 0;
	m.mat[3][2] = 0;
	m.mat[3][3] = 1;
	
	Vector4 Y(0,0,0,1);
	Solve* solve = new Solve(m,Y);
	Vector4 ans = solve->getAns();
	if(ans.v[3] > Config::EPS)
		return MyVec3d(ans.v[0],ans.v[1],ans.v[2]);
	else
		return mid;
}

在calvertexpos中要完成的任务就是返回给它的调用者新顶点的位置，即：数值计算顶点vbar位置使得Δ(vbar)最小，由于Δ的表达式是一个二次项形式，因此令一阶导数为0，求解：

如果系数矩阵可逆，那么通过求解上述方程就可以得到新顶点vbar的位置，如果系数矩阵不可逆，就通过在v1,v2和(v1+v2)/2中选择一个使得收缩代价Δ(vbar)最小的位置。

Matrix MeshSimplify::calVertexDelta(int _id){
	Matrix ans;
	Vertex* p = &(vGroup->group[_id]);
	for(set::iterator it1 = p->connectVertexes.begin();it1 != p->connectVertexes.end();it1++){
		for(set::iterator it2 = p->connectVertexes.begin();it2 != p->connectVertexes.end();it2++){
			if((*it1) < (*it2) && (vGroup->group[(*it1)].isExistConnectVertex(*it2))){
				Vertex* v1 = &(vGroup->group[(*it1)]);
				Vertex* v2 = &(vGroup->group[(*it2)]);
				MyVec3d n = ( (v1->pos) - (p->pos) ).getCross( (v2->pos) - (p->pos)).getUnitVectorOfThis();
				Vector4 tmp(n.x, n.y, n.z, -(p->pos.getDot(n)));
				for(int i = 0;i < 4;i++){
					for(int j = 0;j < 4;j++){
						ans.mat[i][j] += tmp.v[i] * tmp.v[j];
					}

				}

			}
		}
	}
	return ans;
}

在calvertexdelta要完成的任务就是计算收缩边的顶点的误差矩阵Q

void MeshSimplify::calVAndDeltaV(Edge& e){
	Matrix mat = calVertexDelta(e.v1) + calVertexDelta(e.v2);//计算完顶点的误差然后求和
	e.v = calVertexPos(e,mat);//确定一个点收缩后的点	
	Vector4 X(e.v.x, e.v.y, e.v.z, 1.0);
	if (vGroup->getCommonVertexNum(e.v1, e.v2) != 2) {
		e.deltaV = 0;
		return;
	}
	double pri = 0;
	for (int i = 0; i < 4; i++) {
		double p = 0;
		for (int j = 0; j < 4; j++)
			p += X.v[j] * mat.mat[i][j];
		pri += p * X.v[i];
	}
	e.deltaV = pri;
}

在CalVanddeltav要完成的任务就是根据calvertexdelta返回的一条边两个顶点的误差矩阵计算收缩顶点的误差矩阵，然后调用calvertexpos得到收缩边收缩成的新点。之后根据新的边来重新计算delta值。然后我们再来看看初始化的部分：

void MeshSimplify::input(){
	int cntv=0,cntf=0;
	char s[256];
	int tmp = 0;
	while (scanf("%s", s) == 1){
		tmp++;
		switch (s[0]) {
			case '#': fgets(s, sizeof s, stdin); break;
			case 'v': {
				cntv++;
				double x, y, z;
				scanf("%lf %lf %lf", &x, &y, &z);
				vGroup -> addVertex(Vertex(x,y,z));
				break;
			}
			case 'f': {
				cntf++;
				cntFace++;
				int a, b, c;
				scanf("%d%d%d", &a, &b, &c);
				//建立邻接关系,已检查
				vGroup->group[a].addConnectVertex(b);
				vGroup->group[a].addConnectVertex(c);
				vGroup->group[b].addConnectVertex(a);
				vGroup->group[b].addConnectVertex(c);
				vGroup->group[c].addConnectVertex(a);
				vGroup->group[c].addConnectVertex(b);
				break;
			}
			default: break;
		}
	}

	//下面将边加入到边堆中
	for(int i = 1;i <= vGroup->cntVertex;i++){//遍历所有顶点
		for(set::iterator it = vGroup->group[i].connectVertexes.begin();//遍历某个顶点的所有邻接点
			it != vGroup->group[i].connectVertexes.end();it++){
			if(i < (*it))
				break;
			
			Edge e((*it),i);
			calVAndDeltaV(e);//每创建一条边就要计算缩后点和误差
			eHeap->addEdge(e);//将一条边加入其中
		}
	}
	cntDelFace = (int)((1-ratio) * cntFace);//计算应该剩下多少个面
}

这是input函数，前面一大半的部分用来完成作业的要求（读入指定的obj文件）。我们重点关注下边的迭代，它的目的就是根据读入的顶点和面的信息，对每个顶点都计算它和它所有邻接顶点组成的边的误差值，然后加入到所维护的堆中。然后再来看看start

void MeshSimplify::start(){
	for(int i = 0;i < cntDelFace;i += 2){//开始删边	
		Edge e = eHeap->getMinDelta();
		Vertex* v1 = &(vGroup->group[e.v1]);
		Vertex* v2 = &(vGroup->group[e.v2]);
		Vertex v0 = e.v;
		int v0_id = vGroup->addVertex(v0);
		Vertex* pV0 = &(vGroup->group[v0_id]);//定位到缩后的点

		set connectV;//pV0的邻接点
		connectV.clear();
		eHeap->delEdge(e);//打上边已经删除的标记

		for(set::iterator it = v1->connectVertexes.begin(); it != v1->connectVertexes.end();it++){
			if((*it)!=v2->id){
				eHeap->delEdge( Edge((*it),v1->id));
				vGroup->group[(*it)].delConnectVertex(v1->id);
				connectV.insert((*it));
			}

		}

		for(set::iterator it = v2->connectVertexes.begin(); it != v2->connectVertexes.end();it++){
			if((*it)!=v1->id){
				eHeap->delEdge( Edge((*it),v2->id));
				vGroup->group[(*it)].delConnectVertex(v2->id);
				connectV.insert((*it));
			}

		}

		//将原来u，v的结点的邻接点集合中加入新点o
		for (set::iterator it = connectV.begin();it != connectV.end(); it++) {
			vGroup->group[(*it)].addConnectVertex(v0_id);
			vGroup->group[v0_id].addConnectVertex(*it);
		}
		vGroup->isDeleted[v1->id] = true;//标记结点已经被删除
		vGroup->isDeleted[v2->id] = true;

		//给新点加边
		for (set::iterator it = connectV.begin(); it != connectV.end(); it++) {
			Edge e((*it),v0_id);
			calVAndDeltaV(e);
			eHeap->addEdge(e);
		}



	}

}

Start的一开始就是根据现在堆里的信息选择cost最小的边进行删除，对应边置上删除的标记并且得到了我们需要的收缩点的，根据新的点的信息结合原来边的点的邻接点的信息来组成新的边，更新这个信息，最后最重要的，不要忘了根据新的信息维护你的堆，以便下一次迭代使用。

int main(int argc, char* argv[])
{
	string inputname="";
	string outputname="";
	string outputsurfacenumber="";
	//cout<<"输入原obj文件名，结果obj文件名，简化率"<>inputname>>outputname>>outputsurfacenumber;
	const char* inputfile=inputname.c_str();
	const char* outputfile=outputname.c_str();
	const char* simply_rate=outputsurfacenumber.c_str();
	MeshSimplify* meshSimplify = new MeshSimplify();
	freopen(inputfile,"r",stdin);
	freopen(outputfile,"w",stdout);
	meshSimplify->setRatio(atof(simply_rate));//设置简化率
	meshSimplify->input();//读入
	meshSimplify->start();//开始简化
	meshSimplify->output();//输出
	freopen("CON", "r", stdin);
	freopen("CON", "r", stdout);

	objModel.load(outputname);
    glutInit(&argc, argv);
    init();
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutMouseFunc(moseMove);
    glutMotionFunc(changeViewPoint);
    glutIdleFunc(myIdle);
    glutMainLoop();


    return 0;
}

主函数这里主要分为两部分，一部分是上边我们一直在介绍的根据读入的obj文件和化简率，调用input函数根据obj文件构造我们的点边堆等信息，调用start进行化简操作，调用output把我们的信息按obj文件的格式放进新的obj文件中；第二部分对应题目要求的（用opengl实现obj文件的输出）部分，基本按照glut的使用格式来做的，就不在赘述。（特殊提及的是还完成了鼠标控制旋转的功能）

三、样例演示

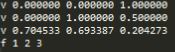
来跑一个简单的obj，一个立方体，它的obj文件内容为：

Opengl显示为

运行代码cmd界面

结果obj的内容为

Opengl显示为

可以看到直接变成一个三角片了

（代码参考：https://github.com/lihy96/MeshSimplify）