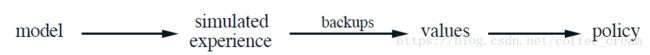8 Planning and Learning with Tabular Methods

【上一节 [7 Multi-step Bootstrapping] (https://blog.csdn.net/coffee_cream/article/details/81053960)】

本节创建了一种统一的方法视图，其中既包括需要一个环境模型）的方法（如动态编程、启发式搜索等，也包括一些不依赖于模型的方法（如蒙特卡洛、temporal-difference等），这里将前者视为是一种 $planning$ 方法，后者视为是一种 $learning$ 方法，这两类方法之间有一些不同点，也有一些相似点，例如，它们的思想的核心都是计算 value functions，并且都是基于对未来事件的展望计算得到一个 back-up value，再利用这个值来更新得到一个近似的 value 函数。前面的章节中介绍了蒙特卡洛方法和 temporal-difference 方法，以及如何用 n-step 方法来统一这两种方法。这一章节也是一种类似的结合方式，它是将 planning 与 learning 方法相结合。在前面的章节中已经介绍了他们的不同点，下面将探讨如何将他们结合在一起。

1、 Models 和 Planning

一个环境的 $model$ 的是指：可以用来预测环境对 actions 的反应的东西，给定一个 state 和一个 action，model可以生成相应的下一个 state 和下一个 reward。如果 model 随机的，那么就有很多种可能的下一个 states 和 rewards，每一种都对应一种发生的概率。有些模型得到的是对所有可能性和概率的描述，这类方法称为是 $distributionmodel$，还有一些模型得到的仅仅是某些可能性，是依据概率进行采样得到的，这类方法称为是 $samplemodels$。例如对股子的和进行预测的模型，一个 distribution model 会得到所有可能的和以及它们发生的概率，而一个 sample model 依据概率分布得到的是一个单独的sum。Distribution model 比 sample model 的能力更强，因为它们总可以用来生成 samples，但在一些应用中，获得 sample model 比 distribution model 要更容易一些，就比如股子的例子，可以利用一个计算机程序来仿真并返回一个sum，而计算得到所有可能的 sums 和对应的概率要更难、更容易出错。

模型可以用来模拟和仿真 experience。给定一个开始的状态和动作，一个采样模型可以生成一个可能的转化，一个分布模型可以生成所有可能的转化（发生的概率作为其权重值）。给定一个初始状态和一个 policy，一个采样模型只可以生成一个 episode，而一个分布模型可以生成所有可能的 episodes 和对应的概率值。无论在哪种情况下，我们都可以说该模型对环境进行了仿真并生成了 simulated experience。

在不同的领域，planning 可以表达不同的意思，这里它代表的是任何一种以 model作为输入，并能生成或提高一种与该环境结合的 policy 的计算过程：

图1

在人工智能领域，有两种不同的 planning 方法，一种是 $state-spaceplanning$，planning 从根本上来讲是根据目标在状态空间中搜索一种更优的 policy 或 path，其中 actions 导致 state 的转变，value function 依据 states 进行计算。另外一种是 $plan-spaceplanning$，planning 是在整个 plans 空间中搜寻，操作者从一种 plan 转化为另一种 plan，并且 value function 是定义在整个 plans 空间中的，plan-space planning 包括 evolutionary 方法和 “partial-order planning”（人工智能领域一种常见的 planning，其中在 planning 的所有阶段 steps 的顺序不是完全决定的），在随机优化控制问题中 plan-space 方法很难有效的应用，因此这里不再详述。

所有的 state-space planning 方法都具有一个统一的结构，主要有两个基本思想：（1）所有的 state-space planning 方法都有一个计算 value functions 的过程，并作为提升 policy 的主要媒介；（2）它们都是利用仿真的 experience 中的 backup 操作来计算它们的 value function。它们的统一结构图如下所示：

图2

Learning 和 planning 的主要思想都是利用 backup 操作来估计 value functions，不同点在于 planning 使用的是模型生成的仿真的experience，而 learning 方法使用的是由环境生成的真实的 experience，由这个不同点就衍生出其他一系列的不同点，如估计 performance 的方法、生成 experience 的方法等等。这个统一的结构意味着很多思想和方法在 planning 和 learning 之间可以传递，特别地，在很多情况下，一个 learning 算法可以由一个 planning 方法的 backup 步骤替换。learning 仅需要 experience 作为输入，并且其他情况下它们可以应用于仿真的 experience 中，就像应用于真实的 experience 中一样。下面的 box 展示了 planning 方法的一个简单的例子，它基于 one-step tabular Q-learning 和采样模型的随机样本，该方法称为是 random-sample one-step tabular Q-planning。

图3

2、Dyna：集成Planning、Acting和Learning

当在线的 planning 完成后，在与环境进行交互的过程中会产生大量的问题，从交互中获得的新的信息可能会改变模型并因此与 planning 交互，因此需要根据当前或将来的状态或决策，以某种方式定制 planning 过程。如果决策的制定和学习模型都是计算密集型的过程，那么可用的计算资源就需要在它们之间进行规划和分配。为了开始探索这些问题，这一节将介绍 Dyna-Q 方法，这是一种简单的框架，它集成了在线 planning 需要的主要函数。下面将主要介绍的是该方法的思想。

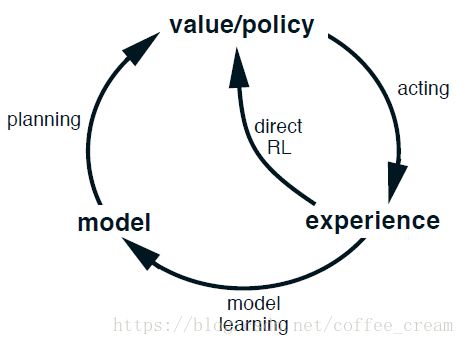
在 planning agent中，真实的 experience 至少有两个角色，它们可以用来提升模型（更确切的说是贴近真实环境状态），并且可以利用一些强化模型方法来直接提升 value function 和 policy。前者我们称为是 model-learning，后者我们称为是 direct reinforcement learning （direct RL）。Experience、model、values 和 policy 直接可能的关系如下图所示，其中每一条箭头代表了一种影响和推测的提升之间的关系，可以注意到，experience 不是直接地就是间接地通过 model 来提升 value 和 policy functions，有时会将后者称为是 indirect reinforcement learning。

图4

不论是 direct 还是 indirect 方法，它们均有各自的优缺点，indirect 方法常常可以充分利用有限的 experience，在与环境很少的交互下就能得到一个更好的 policy；而 direct 方法相比之下更简单，并且不会受模型设计偏斜的影响。有些人认为 indirect 方法总是比 direct 方法更好，而其他人则认为 direct 方法对大部分的人类和动物学习有帮助，心理学和人工智能领域有关的辩论关注的是认知的相对重要性而不是试错学习，以及商议计划而不是反应性决策的制定。这里的观点是，在所有这些辩论中，不同的选择之间的对比被夸大了，通过观测这两种观点之间的相似之处而不是直接反对它们，可以获得更多的洞察力。例如，对动态规划和 temporal-difference 方法，尽管其中一个是为计划而设计的，另一个是用于无模型学习，但这里还是强调了他们之间的相似性。

Dyna 的一般框架如下图所示，Dyna-Q 包含了其中所有的过程：planning、acting、model-learning 和 direct RL，其中 planning 方法是 图4 中给出的 random-sample one-step tabular Q-planning 方法，direct RL 方法是 one-step tabular Q-learning，model-learning 方法也是 table-based 并假设世界是确定性的。在每个 $S_t,A_t\Rightarrow R_{t+1},S_{t+1}$ 转换之后，table 中对 $S_t,A_t$ 的模型记录将用 $R_{t+1},S_{t+1}$ 更新，因此当用已经经历过的 state-action pair 查询 model 时，它会简单的输出之前观测到的下一个状态和奖励作为其预测值。在 planning 过程中，因为 Q-planning 算法只会随机地从之前经历过的 state-action pair 中随机采用，因此该模型永远不会探寻它没有任何信息的 pair。

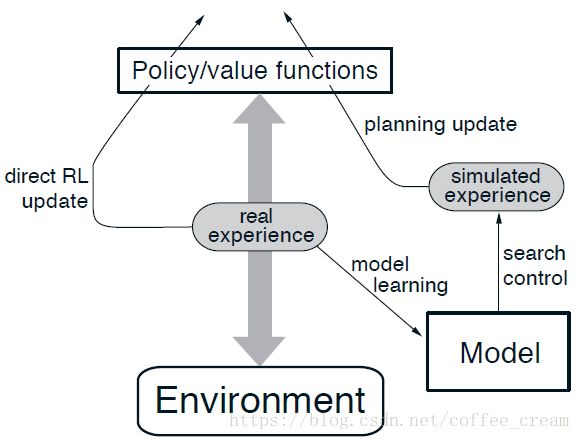
Dyna-Q 算法的全局结构如 图5 所示，中间一列代表了 agent 和 environment 之间主要的交互过程。图中左边的箭头代表了 direct reinforcement learning 通过在真实的 experience 上操作来提升 value function 和 policy，右边的箭头是 model-based 过程。从真实的 experience 中学习得到的 model 生成了仿真的experience，这里用 $searchcontrol$ 代表为仿真的 experience 选择初始的 states 和 actions 的过程，planning 是通过在 simulated experiences 上应用增强学习方法来实现的，这些 simulated experiences 就好像真实发生了一样。和 Dyna-Q 一样，这里用了相同的增强学习方法来学习真实的 experience、来计划仿真的 experience，因此，增强学习方法对 learning 和 planning 来说均为“final common path”，learning 和 planning 在这个意义上是深深整合在一起的，他们具有几乎相同的机制，仅仅是它们的 experience 的来源不同。

图5

从概念上来说，planning、acting、model-learning 和 direct RL 在 Dyna agents 中是连续和并行发生的，虽然如此，但为了串行计算机上的具体实现，在时间点上完全定义了他们发生的顺序。在 Dyna-Q 中，acting、model-learning 和 direct RL 过程仅需要很少的计算资源，因此假设它们只消耗一小部分时间，而其他时间都用到了 planning 过程，planning 本质上就是一个计算密集型的过程。Dyna-Q 的完整算法如 图6 所示，其中，$Model(s,a)$ 代表的是根据 state-action pair $s,a$ 预测下一个状态和 reward 的模型，步骤 (d)、(e) 和 (f) 分别实现了 direct RL、model-learning 和 planning，如果省略掉步骤 (e) 和 (f)，那么剩下的算法就是 one-step tabular Q-learning。

图6

3、当模型错误的时候

最开始的时候模型是空的，之后会用一些信息来填充和构建，但是我们不能保证这些信息是完全正确的，由于环境是随机的，并且我们只观察了有限的样本数量，有可能用近似函数生成的模型是不好的，或者环境发生了变化有些新的行为还未观测到，因此模型有可能是错误的，当模型错误的时候，planning 过程就很有可能计算得到一个非优的策略。

在一些情况下，planning 得到的非优的策略可以很快地发现和纠正模型误差，这种情况是有可能发生的，它往往发生在模型乐观的情况下，即该模型可以预测更好的 reward 或更好的 state 转换。

这里的问题可以一般化为 exploration 和 exploitation 之间的矛盾，在 planning 中，exploration 可以认为是尝试 actions 来提升模型，而 exploitation 可以认为是执行当前模型中优化的方法，我们希望 agent 通过 explore 来发现环境的变化，而不是使性能大大的退化。像前面讲的 exploration 和 exploitation 矛盾一样，可能不存在既完美又实用的解决方法，但简单的启发式方法常常是有效的。

为了鼓励那些长时间没有尝试过的 actions，有一种在仿真 experiences 上使用的方法称为是“bonus reward”，比如，如果对某种转变模型的 reward 为 $r$，并且该转换在过去 $\tau$ 个时间点内都没执行过，那么执行 planning backups 时就假设该转换的 reward 为 $r+\kappa \sqrt{\tau }$，其中 $\kappa$ 的值较小。该方法鼓励 agent 继续测试所有可达的状态转换，甚至为了执行这样的测试而寻找长序列的 actions。当然所有这样的测试都是有其代价的，但在大多情况下，这样的计算是值得额外的探索的。

4、Prioritized Sweeping

在 Dyna agents 中，仿真的转换过程最开始选择的 state-action pairs，是从所有经历过的 pairs 中以均等概率随机选择的，但等概率的选择往往不是最好的方案，当仿真的 transitions 和 backups 专注于特定的 state-action pairs 时，planning 可以更加有效。比如，对第二个 episode，刚开始只有直接通向 goal 的 state-action pair 具有正的 value 值，其他的均为0，也就是说，沿着大部分的 transitions 进行 back up 都是没有意义的，因为它们都是从一个 0 值状态转换到另外一个 0 值状态，这种 backups 没有任何影响作用，仅只有那些通向或开始于 goal 前面的状态的 transitions 才能改变一些 values 值。如果仿真的 transitions 是等概率生成的，那么在发现有用的 backups 之前就会经历很多没有用的 backups，随着 planning 的进行，有用的 backups 区域会增长，但这种方式的效率远远低于专注于好的 state-action pairs 的方式。尤其是在一些真实的问题中，states 的数量巨大，没有专注的查询方式就会非常低效。

因此，如果专注于查询那些目标状态 $backward$ （反向）经过的地方会更有效，当然这里并不是说想利用任何方法来达到目标状态，而是想找到一种适合于一般的 reward 函数的方法，目标状态只是为了方便解释举的一个特殊的例子。一般情况下，我们不仅仅是想从目标状态反向出发，而是从任何一个 value 值改变的状态出发。假设一个模型给出的 value 值最开始都是对的，这时 agent 发现环境发生了变化，之前预测的一个状态的 value 值改变了，那么这就意味着其他状态可能也改变了，此时最有效的 one-step backup 就是那些直接通向value 值改变的状态的 action，当这些 actions 的 values 更新后，前任状态的 value 值也可能会改变，如果是这样的话，那么通向它们的 actions 就需要 back up，之后“它们的”前任状态也可能会改变……，通过这种方式，每次任意从 value 改变的状态反向操作，既执行了有用的 backups，也终止了这种传播过程，这种一般化的思想就称为是 planning computations 的 $backwardfocusing$。

当前面有用的 backups 向后传播的时候，它会迅速的增长，产生有助于 back up 的 state-action pair，当然它们并不是同样有效果的，可能有些状态的 values 值改变的很多，而有的改变的很小，改变量大的 pairs 更有可能在传播中产生更大的 change。在随机的环境中，估计的转换概率的变化会导致改变量的变化，以及 pairs 需要 back up 的重要程度的变化，自然会根据它们的重要程度排序来优先选择那些重要的 backups，这就是 $prioritizedsweeping$ 背后的思想，在该方法中会维持一个队列，任何一个在 back up 后估计的 value 值改变的 state-action pair 均会存入这个队列中，当队列头部的 state-action pair 执行 back up 后，就会计算得到它对前任 pairs 的影响，如果该影响值大于某个阈值，则该 pair 就会以一定的优先值插入队列中（如果队列中之前已经存在该 pair，则队列会保留具有较高优先值的记录）。通过这种方式，改变的影响会有效的向后传播直到收敛，完整的算法如 图7 所示。

图7

5、Planning as Part of Action Selection

Planning 的发展趋势目前主要有两种，一种就是前面介绍的以 dynamic programming 和 Dyna 为典型的方法，它们将 planning 构想是一种策略或 value 函数的逐渐的提升，它一般对所有状态都是有益的，而非专注于某些特殊的状态；另外一种方法认为遇到每个新的状态 $S_t$，计算得到的输出并不是一个真正的 policy，而是一个简单的 action 决策 $A_t$，之后 planning 再更新 $S_{t+1}$ 以生成 $A_{t+1}$，以此类推不断进行下去。这两种 planning 方式可以自然地、有趣地融合在一起，但它们往往是分开研究的。下面将详细介绍第二种方式：$planningaspartofactionselection$

这种情况下 values 和 policy 都是特定于当前的状态和选择的，它们通常在用于选择当前 action 后就被丢弃了，在很多应用中都存在很多种类的状态，在很长一段时间都不太可能会返回到相同的 state，因此这并没有很大的损失。但一般情况下，你可能既希望将 planning 专注于当前的 state，也希望把 planning 的结果存起来以备将来还会返回相同的 state。

在应用中，action selection 中的 planning 是最有用的，一方面是因为它们不要求快速响应，例如在国际象棋游戏里，玩家下每一步都可以考虑几秒钟或者几分钟；另一方面，如果低延迟的 action selection 具有较高的优先级，那么后台通常可以更好的进行 planning 从而计算得到一个策略，然后就可以快速地应用到每一个新遇到的状态中。

6、启发式搜索

人工智能中传统的 state-space planning 方法是 planning-as-part-of-action-selection 方法，也称为是 $heuristicsearch$，在启发式搜索中，对每一个遇到的 state，都会将可能的后续结构构建成一个很大的 tree，在叶节点应用近似的 value function，然后向根节点的当前状态进行 back up。这棵搜索树中的 back up 就和带有 maxes 的 full backups （对 $v_{\ast }$ 和 $q_{\ast }$）一样，back up会在当前 state 的 state-action 节点停止，当计算得到这些节点的 backed-up values 后，会从它们中选择最好的作为当前的 action，最后所有 back-up 值都会被舍弃。

在传统的启发式搜索中，不需要改变近似的 value function 就可以保存 backed-up values，一般情况下，value function 是由人设计的，不会因为搜索的结果而改变，但通常希望可以利用启发式搜索计算得到的 backed-up values 或其他方法来使得 value function 可以随着时间不断提升，从某种意义上说，我们一直都在采用这个方法。尽管规模较小，我们的 greedy 和 $\epsilon -$greedy action-selection 方法与启发式搜索不一样，例如，在给定一个模型和一个 state-value function 的情况下计算 greedy action，我们必须考虑到每一个可能的 action 和每一个可能的下一个 state，对 rewards 和估计的 values 进行 backup，然后从中选择最佳的 action，和传统的启发式搜索一样，该过程会计算所有可能的 actions 的 back-up 值，但不会存储它们，因此，启发式搜索可以看作是 greedy policy 在单步以外的一种思想上的扩展。

搜索多步的目的是为了获得更好的 action selection，如果你有一个很好的模型和一个不太好的 action-value function，那么往往搜索的越深就获得越好的 policies。如果一个搜索总是通向 episode 终点的，那么不太好的 value function 的影响就可以消除，这种方法确定的 action 一定是优化的；如果一个搜索具有充足的深度 $k$，${\gamma }^k$ 就很小，那么 actions 相应也是近似优化的；另一方面，搜索的越深，需要的计算量就越大，常常会导致很长的响应时间。

当然，我们不能忽视启发式搜索关注的 backups 中最明显的方法是针对当前 state 的，启发式搜索的有效性主要是由于它的搜索树紧紧的关注着当前状态后可能立即发生的 states 和 actions。

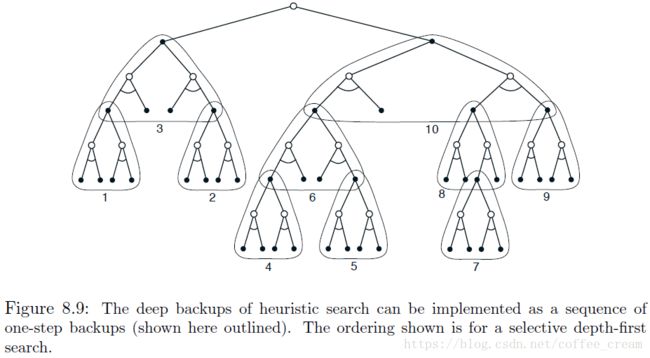
Backups 的分布可以相似的进行修改，主要关注于当前的 state 和其可能的后续版本。作为一个极限的情况，我们可以使用启发式搜索的方法来构造一棵搜索树，然后根据 图8 中所示，从下往上执行单个的一步 buckups，如果 backups 以这种方式排序并使用一种表格的查找方式，那么就会得到与深度优先启发式搜索相同的 backup。任何状态空间搜索都可以以这种方式来思考，它们就像是对大量单独的 one-step backups 进行拼接一样，因此，在 deeper search 中观察到的性能的提升不是由于使用多步 backups，而是由于它对当前状态后续的 state 和 actions 的关注和集中。通过大量与候选 actions 相关的计算，可以得到比无焦点的 backups 更好的决策。

图8

7、Monte Carlo Tree Search

$MonteCarloTreeSearch$ （MCTS）作为 policy 的一部分是 planning 中最简单的例子之一，也是 planning 中最近发展最成功的之一，这在很大程度上得益于计算机的发展，从2005年的业余水平到2015年的一代宗师级别，MCTS 在各种各样的竞争环境中被证实是有效的，在世界的模型完全已知并且计算非常廉价的情况下，它是最常用的一种方法。

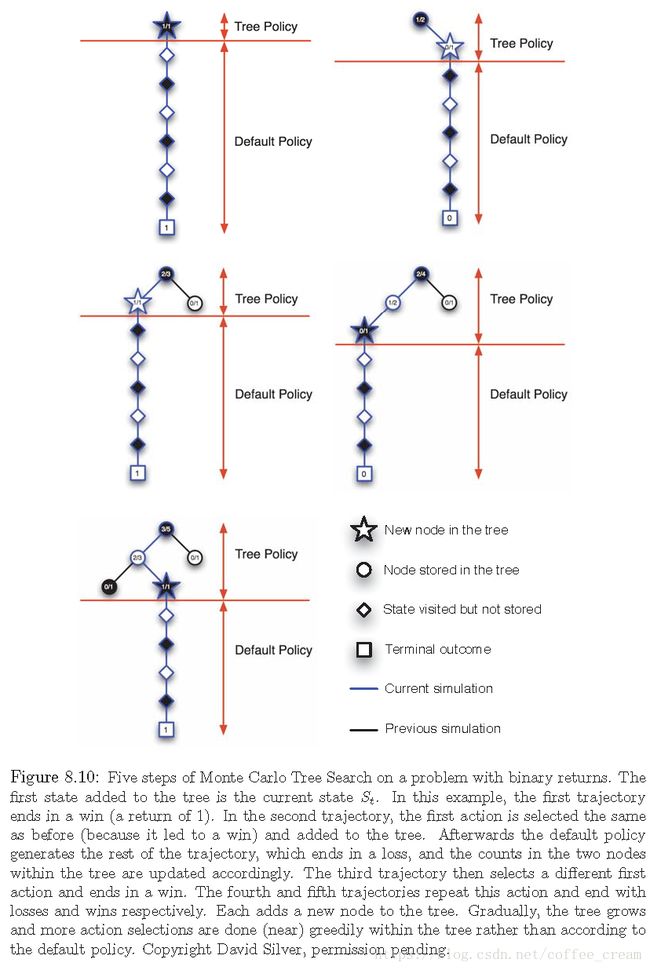
MCTS通常不涉及从一个时间步骤到下一个步骤的近似值函数或策略，这些都是在每一步中计算出来的，然后就会被丢弃。在一个步骤中，许多模拟的轨迹都是从当前状态开始，并一直运行到终端状态（或者直到 discounting 使任何下一步的 reward对 return 的贡献可以忽略不计）。在大多数情况下，轨迹中的 actions 是使用一个简单的 policy 生成的，称为 $defaultpolicy$，其通常是等可能的随机策略。由于这个 policy 和 model 的计算成本很低，因此可以在很短的时间内生成许多模拟轨迹，与任何 tabular Monte Carlo 方法中一样，state-action pair 的估计值为它们（模拟的） return 的平均值。

蒙特卡洛值估计只维护那些最有可能在几个步骤中到达的 state-action pairs 子集，它们形成了一棵以当前状态为根的树，如 图9 所示，任何模拟的轨迹都穿过这棵树，并在某个叶节点上结束，在树的外面和叶节点上会使用 default policy 进行 action selections，但是在树内部的 states 上可以选择的更好，因为对于这些状态，我们至少有一些 actions 的 value 估计值，我们可以用一种知情的方式来从它们中进行选择，例如我们可以使用 $\epsilon$-greedy 方法或 UCB 方法。而对树的边缘的 states，会有一些 actions 没有之前的轨迹，可以认为这些 actions 具有无穷大的 value，那么当其中一个被选中后，就会被添加到树中。初始的树仅仅由当前（根）的 state 组成。

图9

MCTS 通过增量地构建一个局部的游戏树来决定一个游戏程序的进行，每个游戏树的节点代表一个游戏状态，节点之间通过边连接，状态 $s$ 的节点连接到状态 $s’$ 的子节点，对应于状态行为对 $(s,a)$ $a\in \mathcal{A}(s)$，则 $s’$ 是行为 $a$ 产生的下一步状态。在 MCTS 开始时，当前的游戏状态是局部游戏树的根节点，MCTS 的每个迭代过程包括四个阶段：

图10

（1）Selection 利用一些已知的信息在当前树中选择一个节点作为最有希望的节点，以便进一步探索。

（2）Expansion 这棵树通过在被选中的节点下增加一个或几个子节点进行扩展，每个新的子节点此时就成为了这棵局部游戏树的叶节点，也就是说在构建树的时候它的任何可能的动作都还没有被访问过。

（3）Simulation 再一次以已知的信息为指导，从未访问过的 move 中选择一个节点作为仿真的起点，或者一个完整的游戏的 $rollout$ 的开始，这个游戏中的 moves 是通过 $rollout$ policy 选择的。

（4）Backpropagation 利用仿真游戏的结果，通过 back up对 MCTS 迭代中遍历的局部游戏树的 links 的统计信息进行更新或者初始化。在仿真中被访问到的局部游戏树之外的、与状态相对应的链路的统计信息并没有更新。

MCTS 会重复这个过程，每次从局部游戏树的根节点开始，直到时间用完，或者其他的计算资源被耗尽，最后，依据局部游戏树中积累的统计信息，从根节点（仍然代表当前的游戏状态）选择下一个 move，这个 move 就是程序在游戏中实际做出的动作。当对手的 move 产生一个新的游戏状态后，会再次在一棵树上运行 MCTS，这棵树的根节点就代表了新的棋盘状态，并且树中还包含了这个节点的所有后代节点，这些后代节点是在之前游戏的 MCTS 中构建的游戏树中获得的，但除了这些后代节点，其他节点以及相关的统计信息会在这轮中被丢弃。

8、总结

本节强调了 planning 最优行为与 learning 最优行为之间惊人的密切关系，这两种方法都需要对一个相同的值函数进行估计，并且都是在一长串的小型 backup 操作中对估计值进行增量式更新。这使得将 learning 和 planning 过程集成在一起非常简单，只需要允许同时更新相同的估计的 value 函数即可。此外，任何一种 learning 方法都可以转换为 planning 方法，只需要将它们应用于仿真的（仿真生成的） experience 而不是实际的 experience。在这种情况下，learning 和 planning 变得更加相似，它们可能是相同的算法，只是运行的 experience 的来源不同。

在这一章中，我们从不同的维度讨论了 state-space planning 方法中的变量，其中最重要的一个是 buckups 的分布，也就是搜索的焦点，另一个有趣的变量维度是 backups 的大小，backups 越小，planning 方法的增量就越大，最小的 backups 为 one-step sample backups，就像Dyna一样。

参考文献
[1] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto
[2] UCL Course on RL