Java数据结构和算法-图
1.概念
图是一种重要的数据结构,是由顶点的有穷非空集合和顶点之间边的集合组成,由G(V,E)表示,其中G表示一个图,V是该图中顶点的集合,E是图G中边的集合。基本概念包括:顶点,边,有向,无向,权,路径回路,连通域,邻接点,度,入边,出边,入度,出度。
2.存储结构
两种存储结构:邻接矩阵和邻接表。
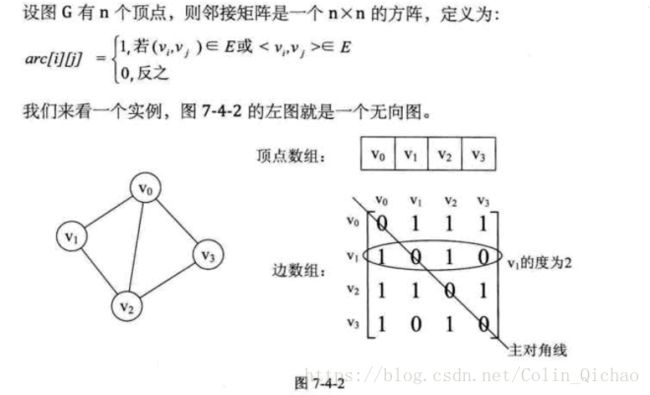
邻接矩阵:
邻接矩阵特征:
1、邻接矩阵是正矩阵,即横纵维数相等。
2、矩阵的每一行或一列代表一个顶点,行与列的交点对应这两个顶点的边。
3、矩阵的点代表边的属性,1代表有边,0代表无边,对角线上对应的横纵轴代表相同的顶点,边没有意义均为0。
4、如果是无向图,那么矩阵是对称矩阵;如果是有向图则不一定。
5、如果是有权图,矩阵点数值可以是权值。
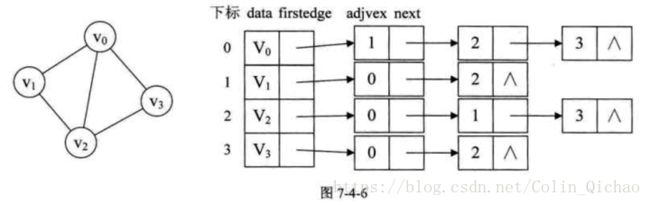
邻接表:
邻接表特性:
1、邻接表示一个有单链表组成的数组 。
2、图中的每一个顶点都有一个链,数组的大小等于图中顶点的个数。
3、无向图的链的第一个元素是本顶点,后继分别连接着和这个顶点相连的顶点;有向图的链第一个顶点是本顶点,后继是以本顶点为起点的边的终点。
4、如果是有权图,可以在节点元素中设置权值属性 。
Java实现图的结构:
package com.binaryTree;
public class Graph {
//顶点数量
private int vertexSize;
//顶点数组
private int[] vertexs;
private int[][] matrix;
//设置不可到达的权值为1000
private static final int MAX_WEIGHT=1000;
public Graph(int vertexSize){
this.vertexSize=vertexSize;
matrix=new int[vertexSize][vertexSize];
vertexs=new int[vertexSize];
for(int i=0;i
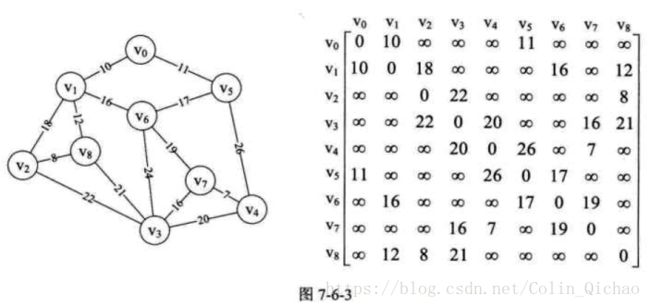
图的遍历:
我们希望从图中某一个顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程称为图的遍历。
两种遍历分别为深度优先算法遍历和广度优先算法遍历:
以该图为例实现两种遍历(注意图有误,v3-v6之间直线应去掉;v0-v8即对应输出0-8)
深度优先算法遍历:
从图中的某个顶点V出发,访问此节点,然后依次从V的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和V路径想通的顶点都被访问到。
package com.binaryTree;
public class Graph {
//顶点数量
private int vertexSize;
//顶点数组
private int[] vertexs;
private int[][] matrix;
//设置不可到达的权值为1000
private static final int MAX_WEIGHT=1000;
private boolean[] isVisited;
public Graph(int vertexSize){
this.vertexSize=vertexSize;
matrix=new int[vertexSize][vertexSize];
vertexs=new int[vertexSize];
for(int i=0;i0&&matrix[index][j]0&&matrix[v][j]
广度优先算法遍历:
从图中的某个顶点V出发,并在访问此顶点之后依次访问V的所有未被访问过的邻接点,之后按这些顶点被访问的先后次序依次访问它们的邻接点,直至图中所有和V有路径相通的顶点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
/**
* 实现广度优先算法遍历
* @param args
*/
public void broadFirstSearch(){
isVisited=new boolean[vertexSize];
for(int i=0;i queue=new LinkedList();
System.out.println("访问到了"+i+"顶点");
isVisited[i]=true;
queue.add(i);
while(!queue.isEmpty()){
u=(Integer)(queue.removeFirst()).intValue();
w=getFirstNeigbour(u);
while(w!=-1){
if(!isVisited[w]){
System.out.println("访问到了"+w+"顶点");
isVisited[w]=true;
queue.add(w);
}
w=getNextNeighbour(u, w);
}
}
}
输出:
访问到了0顶点
访问到了1顶点
访问到了5顶点
访问到了2顶点
访问到了6顶点
访问到了8顶点
访问到了4顶点
访问到了3顶点
访问到了7顶点
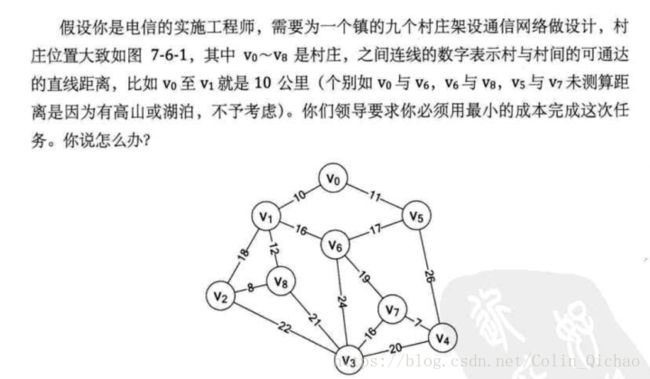
最小生成树:
如图所示我们引入连通图来解决我们遇到的问题,9个村庄对应图上的9个顶点,边表示两个村庄的通信线路,每条边上的权重就是我们搭建这条线路所需要的成本,所以现在我们有9个顶点的连通网可以建立不同的生成树,每一颗生成树都可以作为一个通信网,当我们构造这个连通网所花的成本最小时,搭建该连通网的生成树,就称为最小生成树。生成树是一个极小的连通子图,
生成最小生成树的算法:普里姆算法和克鲁斯卡尔算法(两个算法比较难,只给出实现代码)
Java实现普里姆算法:
/**
* prim 普里姆算法
* @param args
*/
public void prim(){
//最小代价顶点权值的数组,为0表示已不需要考虑
int[] lowcost=new int[vertexSize];
//放顶点权值
int[] adjvex=new int[vertexSize];
int min,minId,sum=0;
for(int i=1;i0){
min=lowcost[j];
minId=j;
}
}
System.out.println("顶点:"+adjvex[minId]+"权值:"+min);
sum+=min;
lowcost[minId]=0;
for(int j=1;j
Java实现克鲁斯卡尔算法:中全ava以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树。称为最小生成树一个连通图的生成树是一个极小的连通有图中全的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树。称为最小生成树一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代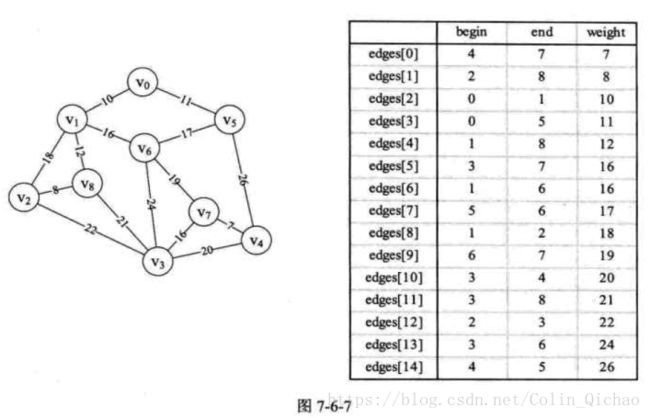 价生
价生
成树。称为最小生成树
package com.binaryTree;
public class GraphKrusKal {
private Edge[] edges;
private int edgeSize;
public GraphKrusKal( int edgeSize) {
this.edgeSize=edgeSize;
edges = new Edge[edgeSize];
}
class Edge{
private int start;
private int end;
private int edgeWeight;
public Edge(int start, int end, int edgeWeight) {
this.start = start;
this.end = end;
this.edgeWeight = edgeWeight;
}
public int getStart() {
return start;
}
public void setStart(int start) {
this.start = start;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
public int getEdgeWeight() {
return edgeWeight;
}
public void setEdgeWeight(int edgeWeight) {
this.edgeWeight = edgeWeight;
}
}
public void createEdge(){
Edge edge0=new Edge(4,7,7);
Edge edge1=new Edge(2,8,8);
Edge edge2=new Edge(0,1,10);
Edge edge3=new Edge(0,5,11);
Edge edge4=new Edge(1,8,12);
Edge edge5=new Edge(3,7,16);
Edge edge6=new Edge(1,6,16);
Edge edge7=new Edge(5,6,17);
Edge edge8=new Edge(1,2,18);
Edge edge9=new Edge(6,7,19);
Edge edge10=new Edge(3,4,20);
Edge edge11=new Edge(3,8,21);
Edge edge12=new Edge(2,3,22);
Edge edge13=new Edge(3,6,24);
Edge edge14=new Edge(4,5,26);
edges[0]=edge0;
edges[1]=edge1;
edges[2]=edge2;
edges[3]=edge3;
edges[4]=edge4;
edges[5]=edge5;
edges[6]=edge6;
edges[7]=edge7;
edges[8]=edge8;
edges[9]=edge9;
edges[10]=edge10;
edges[11]=edge11;
edges[12]=edge12;
edges[13]=edge13;
edges[14]=edge14;
}
/**
* 克鲁斯卡尔算法
* @param args
*/
public void minSpanTreekruskal(){
int n,m,sum=0;
//定义数组,下表为起点,值为终点
int[] parent=new int[edgeSize];
for(int i=0;i0){
f=parent[f];
}
return f;
}
public static void main(String[] args) {
GraphKrusKal graphKrusKal=new GraphKrusKal(15);
graphKrusKal.createEdge();
graphKrusKal.minSpanTreekruskal();
}
}
起始顶点:4结束顶点7
起始顶点:2结束顶点8
起始顶点:0结束顶点1
起始顶点:0结束顶点5
起始顶点:1结束顶点8
起始顶点:3结束顶点7
起始顶点:1结束顶点6
起始顶点:6结束顶点7
最小生成树权值:99 一个连通图的
成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的
最短路径的迪杰斯特拉算法:
package com.binaryTree;
public class GraphDijstra {
private static final int MAXVEX=9;
private static final int MAXWEIGHT=65535;
private int shortTablePath[]=new int[MAXVEX];
/**
* 获取一个图的最短路径
*/
public void shortestPathDijstra(Graph graph){
int min = 0;
int k=0;//记录下表
boolean isgetPath[]=new boolean[MAXVEX];
for(int v=0;vt最小
拓扑排序:
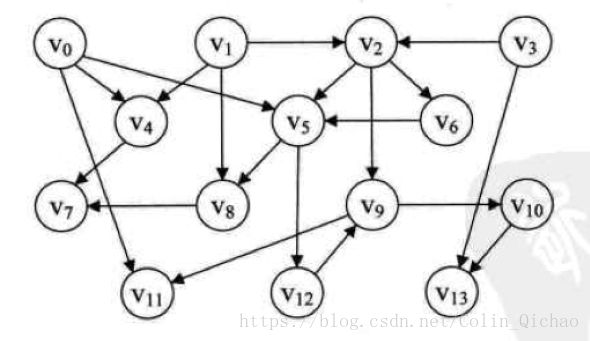
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。
在一个表示工程的有向图中,将顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network),简称AOV网。
一个AOV网应该是一个有向无环图,即不应该带有回路,因为若带有回路,则回路上的所有活动都无法进行(对于数据流来说就是死循环)。在AOV网中,若不存在回路,则所有活动可排列成一个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,我们把此序列叫做拓扑序列(Topological order),由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的,满足上述定义的任一线性序列都称作它的拓扑序列。
Java实现拓扑排序:
package com.binaryTree;
import java.util.Stack;
import com.binaryTree.GraphKrusKal.Edge;
public class GraphTopologic {
VertexNode[] adjList;
//边表顶点
class EdgeNode{
private int adjVet;
private EdgeNode next;
private int weight;
public EdgeNode(int adjVet){
this.adjVet=adjVet;
}
public int getAdjVet() {
return adjVet;
}
public void setAdjVet(int adjVet) {
this.adjVet = adjVet;
}
public EdgeNode getNext() {
return next;
}
public void setNext(EdgeNode next) {
this.next = next;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
}
//邻接顶点(竖着)
class VertexNode{
private int in;//入度数量
private String data;
private EdgeNode firstEdge;//指向出去的顶点
public VertexNode(int in, String data) {
this.in = in;
this.data = data;
}
public int getIn() {
return in;
}
public void setIn(int in) {
this.in = in;
}
public String getData() {
return data;
}
public void setData(String data) {
this.data = data;
}
public EdgeNode getFirstEdge() {
return firstEdge;
}
public void setFirstEdge(EdgeNode firstEdge) {
this.firstEdge = firstEdge;
}
}
private void createGraph(){
VertexNode node0=new VertexNode(0,"v0");
VertexNode node1=new VertexNode(0,"v1");
VertexNode node2=new VertexNode(2,"v2");
VertexNode node3=new VertexNode(0,"v3");
VertexNode node4=new VertexNode(2,"v4");
VertexNode node5=new VertexNode(3,"v5");
VertexNode node6=new VertexNode(1,"v6");
VertexNode node7=new VertexNode(2,"v7");
VertexNode node8=new VertexNode(2,"v8");
VertexNode node9=new VertexNode(2,"v9");
VertexNode node10=new VertexNode(1,"v10");
VertexNode node11=new VertexNode(2,"v11");
VertexNode node12=new VertexNode(1,"v12");
VertexNode node13=new VertexNode(2,"v13");
adjList=new VertexNode[14];
adjList[0]=node0;
adjList[1]=node1;
adjList[2]=node2;
adjList[3]=node3;
adjList[4]=node4;
adjList[5]=node5;
adjList[6]=node6;
adjList[7]=node7;
adjList[8]=node8;
adjList[9]=node9;
adjList[10]=node10;
adjList[11]=node11;
adjList[12]=node12;
adjList[13]=node13;
node0.firstEdge=new EdgeNode(11);node0.firstEdge.next=new EdgeNode(5);node0.firstEdge.next.next=new EdgeNode(4);
node1.firstEdge=new EdgeNode(8);node1.firstEdge.next=new EdgeNode(4);node1.firstEdge.next.next=new EdgeNode(2);
node2.firstEdge=new EdgeNode(9);node2.firstEdge.next=new EdgeNode(6);node2.firstEdge.next.next=new EdgeNode(5);
node3.firstEdge=new EdgeNode(13);node3.firstEdge.next=new EdgeNode(2);
node4.firstEdge=new EdgeNode(7);
node5.firstEdge=new EdgeNode(12);node5.firstEdge.next=new EdgeNode(8);
node6.firstEdge=new EdgeNode(5);
node8.firstEdge=new EdgeNode(7);
node9.firstEdge=new EdgeNode(11);node9.firstEdge.next=new EdgeNode(10);
node10.firstEdge=new EdgeNode(13);
node12.firstEdge=new EdgeNode(9);
}
/**
* 拓扑排序
* @param args
*/
private void topologicSort(){
Stack stack=new Stack();
int count=0;
int k=0;
for(int i=0;i<14;i++){
if(adjList[i].in==0){
stack.push(i);
}
}
while(!stack.isEmpty()){
int pop=stack.pop();
System.out.println("顶点"+adjList[pop].data);
count++;
for(EdgeNode node=adjList[pop].firstEdge;node!=null;node=node.next){
k=node.adjVet;//下标
if(--adjList[k].in==0){
stack.push(k);
}
}
}
if(count<14){
try {
throw new Exception("拓扑排序错误");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
}
public static void main(String[] args) {
GraphTopologic topologic=new GraphTopologic();
topologic.createGraph();
topologic.topologicSort();
}
}
输出:
顶点v3
顶点v1
顶点v2
顶点v6
顶点v0
顶点v4
顶点v5
顶点v8
顶点v7
顶点v12
顶点v9
顶点v10
顶点v13
顶点v11 仅供自己学习笔记。
图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树。称为最小