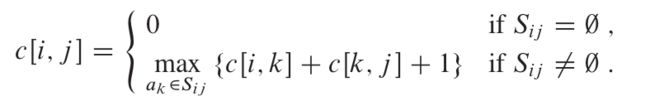贪心：Swift实现

中心思想

求解最优化问题得算法通常需要经过一系列得步骤，每个步骤都面临多种选择。在许多最优化问题上使用动态规划其实会有杀鸡用牛刀的感觉。贪心算法（greedy algorithm）保证每一步都作出当时看起来的最佳的选择，换句话说就是保证局部最优选。

贪心算法一般步骤

确定问题的最优子结构
设计一个递归算法
证明我们每做一个贪心选择，则只剩下一个子问题
证明贪心选择是安全的
设计一个递归算法实现的贪心策略
将递归算法转为迭代算法

明显的通过1，2两步骤的对比，我们知道贪心算法是以DP为基础的。

更一般地，我们可以按如下步骤设计贪心算法：

将最优化问题转为这样的形式：对其做出一次选择后，只剩下一个子问题需要求解。
证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的。
证明做出贪心选择后，剩余的子问题满足性质：其最优解与贪心选择组合即可以得到原问题的最优解，这样就得到了最优子结构。

贪心算法在最优解适用的两个重要性质

贪心选择性质

做局部最优选择来构造全局最优解。即进行选择的时候只需要考虑当前问题中看来最优的选择，而不必考虑子问题的解。

贪心算法进行选择时候可能依赖之前做出的选择，单不依赖任何将来的选择或者子问题的解。贪心算法在进行第一次选择之前不求解任何子问题。一个动态规划算法通常是自底向上进行计算的，而一个贪心算法通常是自顶向下的。通过不断的当前选择来缩小问题的规模。

贪心选择时候要进行众多的选择，这意味着可以改进贪心选择，使其更为高效。可以通过排序跟改变数据结构（通常是优先队列）做到这点。

最优子结构

如果一个问题的最优解包含其子问题的最优解，则称此问题具有最优子结构性质。最优子结构性质是DP与贪心算法的关键。通过最优子结构我们可以设计出递归式来描述最优解值的方法。

贪心中的我们通常使用更为直接的最优子结构。要做的工作转为证明：将子问题的最优解与贪心选择组合在一起能生成原问题的最优解。（数学归纳法的应用）

举个栗子

栗子1）活动选择问题

输入源：活动起始时间数组s，活动结束时间数组f，下标代表第几个活动【注：活动集合 S = {a1, a2, ..., an}，活动ai数据结构为含两个时间的元组，一个为活动开始时间，一个为活动结束时间】。
目标：最大互相兼容的活动集合

牛刀：DP思路

寻找一个最优子结构：
令Sij表示在ai结束之后开，并且在aj开之前结束的活动集合。假设存在Aij子集是我们的解，并且包含活动ak。令Aik = Aij ∩ Sik和Akj = Aij ∩ Skj。 Aij = Aik U {ak} U Akj

反证法可以证明Aij必然包含子问题Sik与Skj的最优解。

递归定义最优解：

自顶向上算法与构造最优解 -> 略

言归正传：贪心选择

我们无需考虑最优子问题就可以选择一个活动加入最优解，原因很简单从人的思维来说，每一个步骤起始就是在选择一个活动，同样是选择一个活动如果这个活动结束的时间越早那么这个活动必然是最优解（反证法）。

1）递归贪心算法

将活动按照活动结束时间进行排序，时间复杂度O(nlgn)。上伪代码：

RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n) //k表示要求解的子问题Sk, n表示问题规模
m = k + 1
while m <= n and s[m] < f[k]
    m = m + 1    // Sk中查找第一个兼容活动ak的活动am，f数组非递减，fi <= fj (i < j)
if m <= n
    return {am} U RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n)
else return NIL

2）迭代贪心算法
RECURSIVE-ACTIVITY-SELECTOR机会就是“尾递归”：结尾的自身递归调用接一次并集操作。而迭代形式更为直接：

GREEDY-ACTIVITY-SELECTOR(s, f)
n = s.length
A = {a1}
k = 1
for m = 2 to n
    if s[m] >= f[k]
        A = A U {am}
        k = m
return A

3）总结
递归与迭代类似，在输入活动已经按照结束时间排序好的前提下，两者运行时间为Θ(n)。

Swift实现

cfunc greedyActivitySelector(starts: [Int], finishes: [Int]) -> [Int] {
    var n = starts.count - 1
    var activities: [Int] = [1]

    var k = 1

    for var m = 2; m <= n; m++ {
        if starts[m] > finishes[k] {
            activities.append(m)
            k = m
        }
    }

    return activities
}

// TEST CASE

var s: [Int] = [0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12]
var f: [Int] = [0, 4, 5, 6, 7, 9, 9, 10, 11, 12, 14, 16]

var a: [Int] = greedyActivitySelector(s, f)

for item in a {
    print("\(item)\t")
}

栗子2）哈夫曼编码

续