ACM 概率&期望
概率&期望
好久没写博客了,最近刷完了概率期望的专题,特地总结一下。
概率
(1) 基本概率知识
学过概率论课程的话,下面的都是基础了。
①条件概率: p(A|B)=p(AB)p(B) p ( A | B ) = p ( A B ) p ( B ) 。
P(A|B) P ( A | B ) 指B发生的条件下A发生的概率。
②全概率: p(A)=∑ni=1p(A|Bi) p ( A ) = ∑ i = 1 n p ( A | B i ) 。
全概率公式的关键在于划分样本空间,需要把所有可能情况不重复、不遗漏地进行分类,并计算出每个分类下事件A发生的概率。
③贝叶斯公式: p(Bi|A)=p(Bi)∗p(A|Bi)∑ni=1p(A|Bi) p ( B i | A ) = p ( B i ) ∗ p ( A | B i ) ∑ i = 1 n p ( A | B i ) 。
④ 古典概型和几何概型:古典概型是最基本的概率计算模型,适用于有限个随机事件的情况,而几何概型则适用于无限个随机事件的情况,几何概型的基本思想是把事件与几何区域对应,利用几何区域的度量来计算事件发生的概率。
(2) 练习
概率问题是一类很常见的问题,大部分都很容易求解。
一般的概率题都只分两种,概率dp,以及普通的概率计算。普通的概率计算,就是应用的基本的概率知识了,不得不说概率论的内容还是挺重要的。概率dp只是状态转移时乘上相应的概率罢了。
uva11722 Joining with Friend
传送门
题意:两人会面,第一个人去的时间在[t1, t2]中,第二个人去的时间在[s1, s2]中,两人会面成功的话,到达会面地点的时间差不能大于w,求两人成功会面的概率。
分析:经典的几何概型,想必数学书上概率部分都有介绍此问题。
几何概型最大的一个特点是通过给定的条件可以将概率分布归于一个几何区域,而所有可能的分布情况也是一个几何区域。那么可以通过几何区域的度量来完成概率计算。常见的一般都是二维随机变量的分布。
本题中情况比较多,考虑需要仔细,计算会面成功的面积可以通过反面来考虑,把不符合的面积减去,每一种概率都不同。
#include xtu 1244 Gambling
传送门
题意:袋子中有a个红球,b个绿球,c个蓝球,不放回地取球,如果某一种球取完了,则游戏结束,先取完红球得一等奖,先取完绿球得二等奖,先取完蓝球得三等奖。求得一等、二等、三等奖的概率。
分析:这题一开始是直接概率dp的。。。然而根本不可做,因为abc范围太大,都达到了1e3,且题目输出的是一个分子/分母的形式,交上去都直接t掉了。。。
要解决还是需要一定的数学基础的。考虑先取完红球的情况,所有可能情况无外乎两种:
(1) 先取完红,在取完绿球,在取完蓝球;
蓝球是最后一个取完的概率是 ca+b+c c a + b + c ,这个概率论课上讲过一个结论,第n次取得蓝球的概率和第一次取得蓝球的概率是相同的,这个可以通过多重集排列证明。
还需要保证绿球晚于红球取完,而绿球在红球和绿球的排列中是最后一个的概率是 ba+b b a + b ,很容易知道这两者的交集包含了所有的先取完红,在取完绿球,在取完蓝球的情况,所以第一种情况的概率就是两者相乘。
(2) 先取完红,在取完绿球,在取完蓝球;
与上面类似,概率为 ba+b+c∗ca+c b a + b + c ∗ c a + c 。
那么先取完红球的概率就是 bc(a+b+c+a)(a+b+c)∗(a+c)∗(a+b) b c ( a + b + c + a ) ( a + b + c ) ∗ ( a + c ) ∗ ( a + b ) 。
先取完绿球和先取完蓝球的概率同理可得分别为 ac(a+b+c+b)(a+b+c)∗(b+c)∗(a+b),ab(a+b+c+c)(a+b+c)∗(b+c)∗(a+c) a c ( a + b + c + b ) ( a + b + c ) ∗ ( b + c ) ∗ ( a + b ) , a b ( a + b + c + c ) ( a + b + c ) ∗ ( b + c ) ∗ ( a + c ) 。
从本题可以看出,在一些概率的计算问题中只要选取合适的分类,那么计算也会相应变得清楚和简单了。培养自己多角度思考问题和观察问题的能力还是很重要的。
#include csu 1917 There is no SSR
传送门
题意:阴阳师抽奖,得到R的概率为p,得到SR的概率为1-p,求抽m次奖连续获得n个SR的概率。
分析:多校时这题题意都没看懂。。。in succession是连续的意思,本蒟蒻一眼看上去以为是成功得到n个SR的概率。。。。。
可以反过来考虑,求出不会连续得到n个SR的概率,这个利用dp便可以很简单的求出了,令dp[i]为抽i次奖不会连续得到n个SR的概率,
#include uvalive6672 Bonus Cards
传送门
题意:有n张票,有a个拥有icpc card的人,b个拥有acm card的人,每次会进行一轮抽奖,拥有icpc card的人抽奖时获得2个slot,拥有acm card的人抽奖时获得1个slot,然后随机选择一个slot,那么这个slot的拥有者得到票,得到票的人下次不会参与抽奖,抽奖的过程在n轮之后或者每个人都得到票之后结束。现在还有一个人,他想知道自己在拥有一张icpc card和一张acm card这两种情况下与这a+b个人来抢票时成功得到票的概率。
分析: 这题是明显的概率dp,在额外一个拥有icpc card的人参与抽奖的情况下,令dpi[i][j]为前i轮有j个拿icpc card的人得到了票的概率。在额外一个拥有acm card的人参与抽奖的情况下,令dpa[i][j]为前i轮有j个拿icpc card的人得到了票的概率。
dp时采用刷表的方式比较方便,这题其实不难,但是比较卡时间。。。。动不动就t了。
考虑几个优化:
①如果dp[i][j]接近0,那么可以不用转移了,因为乘上概率之后更小了,加上去对于1e-9的精度无影响。
②计算时采用乘法比除法更快。
③初始化时只清零能用到的值。
第一个优化节省了接近4000ms的时间。。。
本题的优化方式可以说是非常常见和重要的的,同样地可以利用滚动数组实现空间上面的优化。
#include hdu 5985 Lucky Coins
传送门
题意:有k(k<=10)种硬币,每种硬币的数量和其抛一次正面向上的概率已知。会进行如下的过程:将每枚硬币向上抛一次,每次把正面朝下的硬币给去掉。重复上面的过程直到某一次只剩下了一种硬币或者没有硬币有剩余为止。如果结束时还剩下一种硬币,那么该种硬币即为幸运硬币,现在需要求每一种硬币成为幸运硬币的概率。
分析:一看上去就觉得可做,但是情况比较多,本蒟蒻刚开始也陷在里面了。。
首先这里给出了硬币正面向上的的概率,以及6位精度,我们只需要枚举每枚硬币在i轮死亡,其他硬币在第i轮之前死亡的的情况即可,可以知道i枚举到100也已经more than enough了~所以可以直接dp出每种硬币在第j轮死亡的概率,那么我们然后统计下dp数组的前缀和,然后枚举轮数即可。但是似乎复杂度比较高。
从反面考虑这个问题,不妨这样计算:
令 f[i][j] f [ i ] [ j ] 表示第i枚硬币在前 j j 轮之前死亡的概率。这样 f[i][j]=(1−pij)numi f [ i ] [ j ] = ( 1 − p i j ) n u m i ,这里 pi p i 是第i种硬币正面向上的概率, numi n u m i 是其数量。
令 g[i][j] g [ i ] [ j ] 表示第i种硬币在j轮之后仍然存活的概率,那么 g[i][j]=1−f[i][j] g [ i ] [ j ] = 1 − f [ i ] [ j ] 。
为了不重复统计,我们枚举第i种硬币死亡的轮数。
那么
#include hdu 5955 Guessing the Dice Roll
传送门
题意:有n个长为L的1~6的序列,一直投骰子,并把骰子的数记录下来,当记录下来的序列匹配某一个序列时,游戏结束,求游戏结束后每个序列被匹配的概率。
分析:这里是明显的概率dp,不过注意到这里是匹配问题,我们可以用ac自动机构造当前的状态并向下一个状态转移。在得到方程组之后就可以直接高斯消元了~
//精度要求比较高,消元时的eps要设置小一点,比赛时没注意到这个问题然后一直wa,然后被队友嫌弃…后面把eps改为1e-14就过了。
#include CFGym 100608G Greater Number Wins
传送门
题意:两个玩家玩游戏,每个玩家有一行总共d个格子,会玩两个版本的游戏,第一个游戏中,两个玩家轮流操作,每次操作该玩家随机得到一个0~b-1之间的随机数,然后把这个数填在他自己的一个未被填的格子上,
如果最后两个玩家都填满了d个格子,那么比较两个玩家所得到的d位b进制数,数字大的玩家赢,第二个游戏中,第一个玩家先操作d次,然后第二个玩家操作d次。
求两个游戏中无论第二个玩家如何操作,第一个玩家都能赢的最大概率。
分析:
第一次做asc的题。。果然我这种智商为0的人想的特别简单。。。认为一定把数字大的优先放在高位,这里存在一个明显的问题,游戏都没结束,怎么知道当前抽的这个数字是大还是小。。。
其实是根据样例直接猜测的。。然后第二个样例就wa了。
这样我们自然而然的考虑到了dp,令dp[i][j]表示当前第一个玩家填的数字是i,第二个玩家当前填的数字是j的情况下第一个玩家能赢的最大概率。
这样,我们直接记忆化dp,暴力枚举当前状态下每个人得到的数字以及填的位置,第一个玩家会最大化概率,第二个玩家当然会最小化概率。
这里状态中需要考虑当前位置是否已经填过,我们只需要把数字+1就行了,如果当前位大于0,那么必定是已经填过的。
两种游戏转移过程有点区别而已。
不过快要超时了。。可以把所有可能的情况打个表,情况不过几十种。
#include hdu 5819 Knights
传送门
题意:数轴上有n个骑士位于1,2,3,…n,移动速度相同,初始移动方向已知,当两个骑士相遇时,各有50%的概率赢,输了就死了,并且移动到0和n+1的位置时移动方向会翻转,问最右的骑士存活的概率。
分析:可以发现这个问题中速度和时间都是无关紧要的,第 n n 个骑士如果要赢,那么必然是他向左能打败前面所有存活下来的向右的骑士。
考虑 dp[i][j] d p [ i ] [ j ] 表示前 i i 个骑士有 j j 个是向右走的概率。第 i i 个骑士如果向左,那么有转移 dp[i][j]=∑i−1k=jdp[i−1][k]∗(12)k−j+1 d p [ i ] [ j ] = ∑ k = j i − 1 d p [ i − 1 ] [ k ] ∗ ( 1 2 ) k − j + 1 ,枚举上一阶段有 k k 多少个骑士向右走,那么第 i i 个骑士打败了 k−j k − j 个骑士之后死亡。这里我们可以看出来 dp[i][j]=dp[i][j+1]+dp[i−1][j]2 d p [ i ] [ j ] = d p [ i ] [ j + 1 ] + d p [ i − 1 ] [ j ] 2 。
如果第i个骑士向右,那么 dp[i][j]=dp[i−1][j−1] d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] 。
这里忽略了一种情况,前i个骑士如果最后有1个是向右走,那么也可能是第i个骑士打败左边所有向右走的骑士然后到了0点后反向,那么 dp[i][1]+=∑i−1j=1dp[i−1][j]∗(12)j d p [ i ] [ 1 ] + = ∑ j = 1 i − 1 d p [ i − 1 ] [ j ] ∗ ( 1 2 ) j 。那么合并得到 dp[i][1]=dp[i][2]+dp[i−1][1] d p [ i ] [ 1 ] = d p [ i ] [ 2 ] + d p [ i − 1 ] [ 1 ] 。
最后答案是 ∑n−1i=1dp[n−1][i]∗(12)i,也就是dp[n][1]2 ∑ i = 1 n − 1 d p [ n − 1 ] [ i ] ∗ ( 1 2 ) i , 也 就 是 d p [ n ] [ 1 ] 2 。
#include hdu 4089 Activation
传送门
题意:有n个人排队等着在官网上激活游戏。Tomato排在第m个。
对于队列中的第一个人。有以下情况:
1、激活失败,留在队列中等待下一次激活(概率为p1)
2、失去连接,出队列,然后排在队列的最后(概率为p2)
3、激活成功,离开队列(概率为p3)
4、服务器瘫痪,服务器停止激活,所有人都无法激活了。
求服务器发生瘫痪且这时Tomato在队列中的位置<=k的概率。
分析:感觉很好的一个题,值得一做。
这里不难想到概率dp,令 dp[i][j] d p [ i ] [ j ] 表示队列中当前有 i i 个人,且站在第 j j 个位置上时最终会到达终态的概率。
如果 1<j<=k 1 < j <= k ,那么 dp[i][j]=p1∗dp[i][j]+p2∗dp[i][j−1]+p3∗dp[i−1][j−1]+p4; d p [ i ] [ j ] = p 1 ∗ d p [ i ] [ j ] + p 2 ∗ d p [ i ] [ j − 1 ] + p 3 ∗ d p [ i − 1 ] [ j − 1 ] + p 4 ; 考虑当前状态到达终态由四种转移而来:激活失败、失去连接、服务器瘫痪。
这里 j==1 j == 1 特判一下,有 dp[i][1]=dp[i][1]∗p1+p2∗dp[i][i]+p4 d p [ i ] [ 1 ] = d p [ i ] [ 1 ] ∗ p 1 + p 2 ∗ d p [ i ] [ i ] + p 4 ;
如果 k<j<=i k < j <= i ,那么 dp[i][j]=p1∗dp[i][j]+p2∗dp[i][j−1]+p3∗dp[i−1][j−1] d p [ i ] [ j ] = p 1 ∗ d p [ i ] [ j ] + p 2 ∗ d p [ i ] [ j − 1 ] + p 3 ∗ d p [ i − 1 ] [ j − 1 ] ;那么当前状态不可能通过服务器瘫痪到达终态。
这里,我们令 tp2=p2/(1−p1),tp3=p3/(1−p1),tp4=p4/(1−p1)。 t p 2 = p 2 / ( 1 − p 1 ) , t p 3 = p 3 / ( 1 − p 1 ) , t p 4 = p 4 / ( 1 − p 1 ) 。
到了这里,我们仍然不能直接递推求解,因为 dp[i][j] d p [ i ] [ j ] 依赖于 dp[i][j−1] d p [ i ] [ j − 1 ] ,而 dp[i][1] d p [ i ] [ 1 ] 依赖于 dp[i][i] d p [ i ] [ i ] ,递推关系成环,那么是否需要高斯消元?
当然不需要,高斯消元也无法承受这样规模的数据量,这里我们得到了有了未知数方程,当然可以直接解决。
为了方便考虑,我们在计算 dp[i][j] d p [ i ] [ j ] 时,将这一个方程组中所有的已知量用 v[j] v [ j ] 表示。
那么现在方程组就变为了
从 dp[i][i] d p [ i ] [ i ] 开始,不断地利用②式迭代最终可以得到 (1.0−(tp2)i)dp[i][i]=∑ij=1c[j]∗(tp2)i−j。 ( 1.0 − ( t p 2 ) i ) d p [ i ] [ i ] = ∑ j = 1 i c [ j ] ∗ ( t p 2 ) i − j 。
解出 dp[i][i] d p [ i ] [ i ] ,然后就可以得到 dp[i][1] d p [ i ] [ 1 ] ,最终递推出所有的 dp[i][j] d p [ i ] [ j ] 。
最终答案就是dp[n][m]。
这一题,不仅需要对概率dp有熟练的掌握,而且还要学会如何化简递推方程,从而解出所有变量。
#include 期望
(1) 基础知识
①离散随机变量的期望为该随机变量所有的值与概率的加权的和,连续型随机变量的数学期望为 ∫+∞−∞xf(x)dx ∫ − ∞ + ∞ x f ( x ) d x ,f(x)为随机变量x的概率密度。(数学期望只有在收敛的情况下才存在。)
②期望的性质:
若随机变量X,Y相互独立,则E(XY) = E(X)E(Y)。
E(AX + BY + C) = AE(X) + BE(Y) + C。
③全期望:把所有可能情况不重复、不遗漏地分成若干类,每类计算数学期望,然后把这些数学期望按照每类的概率加权求和即可。
(2) 练习
数学期望的计算一般都不难,但部分题还是比较考验数学能力的。
uva12230 Crossing Rivers
传送门
题意:一人住在村庄A,每天要去村庄B上班,AB之间的距离为D,默认在陆地的速度为1,AB之间有N条河,给出N条河的信息,包括起始坐标p,宽度L,以及河中船的速度。出门前所有船在河中位置是随机的(包括方向)。求从A到B所需要的期望时间。
分析:连续随机变量均匀分布下的数学期望,很容易知道期望在L/v和3L/v之间均匀分布,那么E = 3Lv+Lv2 3 L v + L v 2 ,根据期望的线性性质,把过每一条河的数学期望值加起来即可。
#include uva1639 Candy
传送门
题意:两个盒子各有n个糖,每天随机选一个盒子打开,打开第一个盒子和第二个盒子的概率分别为p,1-p,某一天打开发现之后发现盒子里面没糖了,求此时另外一个盒子里面糖数的期望。
分析:二项分布下的数学期望,如果最后第一个盒子没糖了,则第二个盒子里面糖数的个数可能为I = 0,1,2,3,……n,相应地概率为 (2n−in)∗pn+1∗(1−p)n−i ( 2 n − i n ) ∗ p n + 1 ∗ ( 1 − p ) n − i ,则
Ps:题目很简单,但是本题涉及到一个重要的防止运算溢出和保存精度的技巧:取对数。通过对数,指数运算、乘除法的溢出都可以避免。还有一点就是本题有一个很容易忽视的问题,最后打开盒子时发现没糖了,因此该盒子打开过n+1次,不要想当然写成n次。。。细节问题不容忽视!(傻逼的我经常犯这种错-_-)。
#include uva10900 So you want to be a 2n-aire?
传送门
题意:一个娱乐节目中,刚开始玩家初始的金额为1,有n道题目,答对每一道题目的概率在t到1之间均匀分布,每答一道题,答对的话奖金翻倍,答错的话结束游戏,一分也拿不到。每次听到问题后可以选择答题与不答题,不答题则游戏结束。求玩家在最优策略下能获得的奖金的期望值。
分析:这个题还是比较好的,因为要考虑连续概率下的最大期望情况。考虑一种简单的情况,每次答对题的概率固定,假设为p,那么能获得的最大期望奖金值是多少呢?
当前答到第i题能获得最大期望奖金是多少呢?ans = p * 答对第i题之后能获得最大期望奖金。这是很明显的递推了,所以可以令dp[i]为答对前i题能获得的最大期望奖金。那么
dp[i]=max(2i,0∗(1–p)+p∗dp[i+1]) d p [ i ] = m a x ( 2 i , 0 ∗ ( 1 – p ) + p ∗ d p [ i + 1 ] ) 。不答题 2i 2 i ,答题时这个递推是很清晰的,总共两种情况,没答对0元,答对了钱就是dp[i+1]了,dp[n] = 2n 2 n ,逆推,dp[0]即为答案。
知道了上述之后,考虑连续概率的情况。本题加上连续概率纯粹是为了加大难度,但是要取最大的话,那么做最优策略就行了,可以计算出每次的临界概率,也就是令 s=2idp[i+1] s = 2 i d p [ i + 1 ] 如果s <= p,也就是答题能获得更大的期望值,那么选择答题,均匀分布下 dp[i]=max(2i,t+12∗dp[i+1])=t+12∗dp[i+1] d p [ i ] = m a x ( 2 i , t + 1 2 ∗ d p [ i + 1 ] ) = t + 1 2 ∗ d p [ i + 1 ] ,如果s > p,则在[p, s]这一段概率分布下最优策略当然是不答题,[s, 1]这一段概率分布下选择答题,取全期望可得
Ps:本题还是值得学习的,学会从简单的问题着手考虑,把复杂的问题分解至简单的问题,细心的分析同样是必不可少的!
#include LightOJ 1151 Snakes and Ladders
传送门
题意:有100个格子,从1开始走,每次随机向前走1~6步。某些格子是可以传送的,即到达之后会立即被传送至另一个格子,给定这些传送的情况,问从1号格子走到100号格子所需要的期望步数。
分析:很明显的递推,令dp[i]表示当前在i号格子时走到100号格子还需要扔骰子的期望次数。
那么如果i这个格子没传送,则 dp[i]=∑kj=1dp[i+j]+6k d p [ i ] = ∑ j = 1 k d p [ i + j ] + 6 k ,否则dp[i] = dp[g[i]],注意到一个问题,本题dp[i]的依赖是成环的,不能直接递推解决,需要建立矩阵高斯消元。
不过,我就不明白为何用全主元消去法就是wa,真是不明白了。。。
Ps:本题算是一个代表吧,如果递推关系成环,则需要进行消元求解。
#include LightOJ 1274 Beating the Dataset
传送门
题意:给定0和1的个数,这些0、1产生的任何一个多重集排列都是可能的,求所有可能的n位01排列中第一位为0的位或者与排列中前面一位不同的位的期望个数。
分析:假设有x个i,y个j,本题有两种方法:
(1) 直接进行期望dp,这个递推也是清楚的,令dp[i][j][k]为前i位中有j个1且第i位为k时还会产生的期望个数。
那么当前有x-i个1没填,y-(i-j)个0没填,那么
(2) 计算贡献和,只有两种情况:
①第一位为0,此时对答案的贡献和即为概率p = yn y n 。
②排列中包含一个0和1,且0和1相邻,对期望的贡献和为概率
所以 E=yn+2∗x∗yn=2∗x∗y+yn E = y n + 2 ∗ x ∗ y n = 2 ∗ x ∗ y + y n 。
Ps:本题中计算贡献和的思路值得学习,即期望的线性可加性,从整体出发,把情况分类,每类计算期望,最后求和即可。
#include #include LightOJ 1265 Island of Survival
传送门
题意:岛上面有t只老虎,一个人,d只鹿,每天随机有两个动物会面:
1.老虎和老虎碰面,两只老虎就会同归于尽;
2.老虎和人碰面或者和鹿碰面,老虎都会吃掉对方;
3.人和鹿碰面,人可以选择吃或者不吃该鹿;
4.鹿和鹿碰面,相安无事;
求最后人活下来的最大期望概率。
分析:和上题一样,本题有两种方法:
(1) 直接期望dp,令dp[i][j]表示岛上现在有i只老虎和j只鹿时人活下去的期望概率,根据碰面的可能情况转移即可,至于人遇到鹿这种情况在杀鹿和不杀鹿之间取较大值即可。
(2) 完全可以通过分析得出概率,如果老虎数量为奇数,肯定不可能活下去,为偶数的话只有所有老虎两两同归于尽才有活下去的可能性。只有老虎会对人活下去产生影响,鹿可以不用考虑(此时样本空间发生了变化),所以算出老虎同归的概率即可。每次两只老虎同归于尽的概率为(C_t^2)/(C_(t+1)^2 ),概率全部相乘即可。
Ps:本题值得学习的一点是第二种方法,这个是从题目出发对问题进行简化的思路,因为理论分析保证了简化问题的正确性。
#include #include LightOJ 1284 Lights inside 3D Grid
传送门
题意:一个X*Y*Z的网格,每个位置(x, y, z)上都有一盏灯,初始时所有灯都是灭的,进行k轮操作,每次选择(x1, y1, z1)和(x2, y2, z2),然后把所有(x, y, z)位置的灯的状态都改变,min(x1, x2) <= x <= max(x1, x2),y、z范围同理。
分析:可以考虑dp,但是一个问题就是每个格子的状态对于新一轮的操作而言都是必须记录的,dp状态无法表示。
那么只能单个考虑了,也就是说从整体出发,计算每个格子对于最终答案的贡献和,分别求出期望最后相加即可。
对于格子(x, y, z)而言,令dp[i]为i次操作后其被改变奇数次的概率,dp[i] = (1-p) * dp[i-1] + p * (1 – dp[i-1]),p为进行一轮操作该盏灯被改变的概率,上述递推式可以简化至O(1),不断地迭代可以得到 dp[i]=1−(1−2p)i2 d p [ i ] = 1 − ( 1 − 2 p ) i 2 , 这样的话复杂度变为O(XYZ)。
至于p的计算,只要每一维下都被选中就行了,也就是含1到n这条数轴上任意选择两点,求其包含给定点的概率。容易知道
至此,本题已经完成。
关键的两点:①单独考虑计算贡献和;②化简递推式;
ps: 化简递推式依稀记得离散数学课上讲过。。。不过忘得差不多了,才发现居然是如此的有用!所以说,知识和经验才是解题的王道。
#include LightOJ – 1287 Where to Run
传送门
题意:给定一个无向图,你抢劫了银行,警察正在追你,首先你在0号点,每次你都会往邻接的点跑,去往一个点的条件是从该点出发能走完所有的安全的点(没有警察的点称为安全的点,每次你离开一个点,该店就会被警察占领),把这样的点称为Ej点,如果当前点邻接的EJ点的个数为0的话,你就会被抓住,否则可以等概率地呆在原地5分钟或者往任意一个EJ点走,求警察抓住你的期望时间。
分析:明显的状压dp,令dp[i][s]为当前走完了s当中的点且在i号点时警察抓住你还需要的期望时间。那
题目有一个坑点:如果一个点没有其他点可以到达,直接输出0就可以了!(被坑了好久。。。)
#include short vis[N][1<int p[N];
int n, m;
struct edge { int v, w; };
vector LightOJ – 1342 Aladdin and the Magical Sticks
传送门
题意:有n根棍子,每根棍子都有一个重量,且要么是可识别的,要么是不可识别的,抽到了可识别的棍子,就不放回,抽到了不可识别的,就要放回,问所有棍子都至少被抽过一次后的获得的期望重量。
分析:本题有两种解法:
(1) 期望dp,刚开始一直在纠结与数据量如此大,无法进行状压,但是其实是可以不用具体考虑每一根棍子的,因为每根不可识别的棍子被抽到的次数是完成相同的,那么只要算其平均值就行了,至于可识别的棍子,只会取一次。
假设ave0为可识别的棍子的平均重量,ave1为不可识别的棍子的平均重量,有x根可识别的棍子,y根不可识别的棍子。
令dp[i][j]为拿了i种棍子且有j跟可识别的棍子时还可以得到的期望重量。
那么
使用滚动数组优化即可,答案即为dp[0][0]。
(2) 求每个棍子的贡献和,可识别的棍子的期望抽到次数为1次,而不可识别的棍子的期望抽到次数就是调和级数的第n项。
此结论来源于邮票收集问题:总共n张邮票,有放回地随机抽取一张邮票,那么每张邮票都被抽到过一次时每张邮票的期望被抽到次数为H(n) = 1 + 1/2 + 1/3 +….. + 1/n。所以全期望求和即可。
Ps:本题值得学习的是第一种方法:因为被抽到的次数都是相同的,那么最后的期望和可以通过从平均权值来求得,这样就可以不用具体考虑每一根棍子了,而只要考虑其类型,这在数学上是完全等价的。不过第二种方法的结论值得了解下。
#include#include 10、csu 1818 Crusher’s Code
传送门
题意:给定一个序列,然后给两个排序算法,求两种算法给序列排好序所要进行的期望迭代次数。
while (!sorted(a)) {
int i = random(n) ;
int j = random(n) ;
if (a[min(i,j)] > a[max(i,j)])
swap(a[i], a[j]) ;
}
Carlos, inspired, came up with the following code:
while (!sorted(a)) {
int i = random(n-1) ;
int j = i + 1 ;
if (a[i] > a[j])
swap(a[i], a[j]) ;
}
分析:期望dp,需要解决的是如何表示当前排列的状态,这个可以通过n进制压缩和康托展开来解决。
#include 11、HDU 4579 Random Walk
传送门
题意:元芳在一条链上走,链有n个点,假设当前在点i,每一秒他走到点j的可能性如下:
求从1号点走到n号点所需要的期望时间。
分析:本题思路还是很清晰的,期望dp,但是问题在于高斯消元复杂度太大,只能采用其他方法解决。观察到这个方程是有特点的,dp[i]只与dp[i-m]~dp[i+m]相关且m很小,完全可以直接暴力消元。具体做法:
首先建立好所有的dp方程,然后从n-1行开始消元,每次消掉一个变量即可,最后消至第一行可以解得dp[1]。
假设n为5,m为2,考虑如下的方程:
p11x1+p12x1+p13x3=b1; p 11 x 1 + p 12 x 1 + p 13 x 3 = b 1 ;
p21x1+p22x2+p23x3+p24x4=b2; p 21 x 1 + p 22 x 2 + p 23 x 3 + p 24 x 4 = b 2 ;
p31x1+p32x1+p33x3+p34x4+p35x5=b3; p 31 x 1 + p 32 x 1 + p 33 x 3 + p 34 x 4 + p 35 x 5 = b 3 ;
p42x2+p43x3+p44x4+p45x5=b4; p 42 x 2 + p 43 x 3 + p 44 x 4 + p 45 x 5 = b 4 ;
x5=0; x 5 = 0 ;
对于第i行,向上消去所有包含 xi x i 的方程,这样可以把 xn−1 x n − 1 ~ x2 x 2 都消去,复杂度为O(nm)。
#include Ps:本题说明了一个常见的问题:普通性的方法效率往往不够高,但至少通用性强且很方便,就好比stl泛型容器一样。高斯消元在解一些很规则的矩阵时效率低下,这时候就要观察矩阵的特点使用高效的方式消元了。
常见的另外一种规则矩阵便是三对角矩阵。
所谓三对角矩阵就是如下形式的矩阵:

一般性公式:


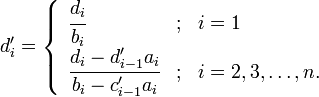
![]()
求解代码如下:
double x[1010], a[1010], b[1010], c[1010];
void tdma(int n) {
c[0] /= b[0]; x[0] /= b[0];
for (int i = 1; i < n; i++) {
double m = 1.0 / (b[i] - a[i] * c[i - 1]);
c[i] = c[i] * m;
x[i] = (x[i] - a[i] * x[i - 1]) * m;
}
for (int i = n - 1; i; i--) x[i] = x[i] - c[i] * x[i + 1];
}可以参考传送门
Ps:本题再次遇到了一个常见的问题:直接计算往往不好处理或者复杂度太高,但我们可以转换下角度,求贡献和。贡献和顾名思义,把总情况归类到有限个个体上,只要对每个个体,我们分别统计贡献,然后把所有的贡献加起来就是最终的答案,这是一个常见的求解方法。
(本蒟蒻举个简单的例子。。。)
现在有n(n <= 100000)种物品,编号1到n,m(m <= 10000)个人拥有这些物品中的一种或几种,这m个人拥有的物品的总个数为w(w <= 1000000)个,给定你每个人拥有的物品的情况,现在要你求每种物品有多少个人有?
通俗的想法是对n种物品,每次询问m个人是否有,这样会有nm次统计。何不转换下角度,如果某个人拥有了一种编号为id的物品,那么直接ans[id]++,最后ans[i]不就是第i种物品有多少个人拥有了吗?这样复杂度就是O(w)。
例子看起来很幼稚,但是却是从贡献出发的一个最直接体现。
可以通过下面的几个题巩固和理解贡献和的计算思路。
Gym 101194H Great Cells
https://vjudge.net/problem/Gym-101194H
题意:N*M的网格,每个格子可以填1~k,定义一个格子为great cell当且仅当该格子中的数比同一行同一列的其他数都大。然后定义A_g为刚好有g个great cell时的填法总数。
最后求 ∑NMg=0(g+1)∗Agmod(1e9+7) ∑ g = 0 N M ( g + 1 ) ∗ A g m o d ( 1 e 9 + 7 ) 。
分析:初看起来求解式如此复杂,但分析可以发现题目是故意设计一个A_g的。想必是为了增加表面上的难度,抓住了关键就变得简单了。
首先可以得出最基本的一个结论,当g>min(N, M)时, Ag A g 为0。其次,观察这个式子, ∑NMg=0(g+1)∗Ag=∑NMg=0g∗Ag+∑NMg=0Ag ∑ g = 0 N M ( g + 1 ) ∗ A g = ∑ g = 0 N M g ∗ A g + ∑ g = 0 N M A g ,很容易知道 ∑NMg=0Ag ∑ g = 0 N M A g 就是所有可能的填法总数。而 ∑NMg=0(g+1)∗Ag ∑ g = 0 N M ( g + 1 ) ∗ A g ,可以知道当有g个great cells时, g∗Ag g ∗ A g 就是某个格子为great cells,且还存在(g-1)个great cells时的总数目,也就是说 g∗Ag g ∗ A g 使得每个格子在刚好有g个great cells时的所有可能情况下都被单独计算了一次,所以 ∑NMg=0(g+1)∗Ag ∑ g = 0 N M ( g + 1 ) ∗ A g 也就是说每一个格子为great cells时的所有可能情况。那么考虑每个格子对答案的贡献和,某个格子成为great cells的总数目为 ∑k−1i=1iN+M−2∗kNM−N−M+1 ∑ i = 1 k − 1 i N + M − 2 ∗ k N M − N − M + 1 。这样最终 ans=N∗M∗∑k−1i=1iN+M−2∗kNM−N−M+1+kNM a n s = N ∗ M ∗ ∑ i = 1 k − 1 i N + M − 2 ∗ k N M − N − M + 1 + k N M 。
这样,我们绕开了 Ag A g 的计算,简化了问题,从计算贡献出发找到了等价的计算式。
#include Csu 1910 Xor Sum
传送门
题意:定义 f(x)=∑n−1i=0dixordn−i−1 f ( x ) = ∑ i = 0 n − 1 d i x o r d n − i − 1 ,d_i表示x的每一位。比如说f(123) = 1^3 + 2^2 + 3^1 = 4。
给定L,R,求f(L) ~f(R)的和。
分析:本题属于比较复杂的与数位有关的题了,可以进行数位dp,但是我们同样可以从计算贡献和的角度出发。
定义solve(x)为f(1)~f(x),如果求solve(x)呢。
假设x = d1d2d3…….dn d 1 d 2 d 3 … … . d n 。令a[i] = ∑9j=0ixorj ∑ j = 0 9 i x o r j 。
①我们首先可以计算1位到n-1位的贡献和。
假设当前计算m位,第一位 d1 d 1 可以填1~9,最后一位 dm d m 可以填0~9,所以 d1和dm d 1 和 d m 对答案产生的贡献是 ∑9i=1a[i]∗10m−2 ∑ i = 1 9 a [ i ] ∗ 10 m − 2 ,而 d2和dm−1 d 2 和 d m − 1 可以随便填,所以总贡献是 (∑9i=0a[i])∗10m−4∗90 ( ∑ i = 0 9 a [ i ] ) ∗ 10 m − 4 ∗ 90 ,乘上90是因为 d1和dm d 1 和 d m 共90种可能。同理, d3和dm−2 d 3 和 d m − 2 …..等都一样。
②考虑n位数字时的贡献和。
从高位枚举到低位,假设当前处于第j位,则此时前面有j-1位已经确定,即为 d1d2d3…….dj−1 d 1 d 2 d 3 … … . d j − 1 。
如果 dj d j 不为0,那么有:
假设j <= n/2,有
考虑i从第1到j-1位, di和dn−i+1 d i 和 d n − i + 1 产生的总贡献为 ∑j−1i=1a[di]∗10n−j∗dj ∑ i = 1 j − 1 a [ d i ] ∗ 10 n − j ∗ d j 。
考虑第j位,可以填0~d[j],产生的总贡献为 ∑dj−1i=0a[i]∗10n−j ∑ i = 0 d j − 1 a [ i ] ∗ 10 n − j 。
考虑i从第j+1位到n/2位,产生的总贡献为 (∑9i=0a[i])∗10n−j∗dj ( ∑ i = 0 9 a [ i ] ) ∗ 10 n − j ∗ d j 。
假设j>n/2,有
考虑i从第1到n-j位, di和dn−i+1 d i 和 d n − i + 1 产生的总贡献为 ∑n−ji=1a[di]∗10n−j∗dj ∑ i = 1 n − j a [ d i ] ∗ 10 n − j ∗ d j 。
考虑第n-j+1位, dj和dn−j+1 d j 和 d n − j + 1 产生的总贡献为 ∑dj−1i=0ixordn−j+1∗10n−j ∑ i = 0 d j − 1 i x o r d n − j + 1 ∗ 10 n − j 。
考虑i从第j+2位到第n/2位,产生的总贡献为 ∑n/2i=j+2dixordn−i+1∗10n−j∗dj ∑ i = j + 2 n / 2 d i x o r d n − i + 1 ∗ 10 n − j ∗ d j 。
还有一个问题就是当n为奇数,且j刚好为n/2+1时,是没有统计的,需要加上去。
计算的时候只统计到了n/2,后面的是对称的,需要乘上2。本身的f值也没有加上去,加上去即可。
前面的过程看起来比较复杂,但基本思路就是,在每一种小于x的情况下,统计所有可能的数位的贡献和。当前为n位时,从高位枚举到低位,基本情况是当前有j-1位已经确定,第j位可以填0~ dj−1 d j − 1 ,后面的第j+1到第n位可以随便填,计算时需要分情况统计。至于位数小于n的情况,只要第一位确定即可,后面可以随便填。
#include 13、hdu 6052 To my boyfriend
传送门
题意:给定一个n*m(1<=n,m<=100)的矩阵,每个格子有一个数字,现在随机选择一个子矩阵,求矩阵里面不同的数字个数的期望。
分析:多校的题。。。看都没看。。。太弱了,没时间来看其他的题。
暴力枚举所有矩阵在判断显然是不可取的,复杂度过高。
这个显然可以用到求贡献的思路。对于每一种数字,我们统计有多少个子矩阵会包含它,根据期望的线性可加性,答案就是每种数字被包含的概率之和了。
标程的思路很巧妙,虽然不是最优的做法,在此采用标程的解法。
对于每一种数字,假设现在数字值为va,首先统计其个数x:
①如果x<=13,这样我们可以容斥求得有多少个子矩阵会包含该数字:加上包含一个该数字的矩阵个数,减去包含两个该数字的矩阵个数,加上三个……这样复杂度最高O( 213 2 13 )。
②如果x>13,那么计算量会大于10000,然而我们可以从反面出发,算出有多少个子矩阵不包含该数字,然后用全部的矩阵个数减去即可,这里有O(nm)的做法,最坏情况也小于等于10000。
枚举每一个格子,我们统计以该位置为右下角时不包含数字va的子矩阵个数。注意到一个子矩阵之间格子是连续的,这样我们可以采用类似扫描的思想。
从上到下,从左到右枚举每个格子:
以c[i][j]表示以(i, j)这个格子为右下角时,往上能延伸的最大高度。
我们需要统计当前格子往左能延伸的宽度,对于每个高度其往左能延伸到的位置是可以得出的,每个格子下往左形成的是一个独立的矩阵块,而且这些矩阵块的数量和位置随着j的增加是会不断变化的。
我们可以以h[i]来表示在第i个矩阵块往上能延伸的高度。以w[i]来表示在h[i]高度下往左能延伸的宽度。
这样如果一个格子左边能延伸的最大高度大于等于当前的c[i][j],那么显然这个是可以合并的,这样合并的时候统计好宽度即可,而j位置以前的矩阵块的信息我们已经得知。
那么这样似乎会出现一种情况,也就是说前面的某一个矩阵块p的高度小于c[i][j],这样不能合并了,但是从(i, j)到该位置p也是能形成符合条件的子矩阵的(高度就是p的高度),但是我们发现这个矩阵的数目就是p这里能形成的矩阵数目,而这个数量在之前是已经统计过了的。
对于每一行的情况都是独立的,我们在每一行扫描时,设置一个变量s,这个s保存了到右下角在第i行时能形成的子矩阵的总数量。在某个格子往左合并的时候,我们减去h[i]*w[i],那么最后s的数目就是不能往左合并矩阵块时能产生符合条件的子矩阵的个数,处理完当前格子之后加上h[now]*w[now]。
本题思路确实很巧妙,自己画个草图模拟下过程就会一目了然。
通过分析,分情况采用最优策略,从正面考虑的容斥原理和从反面考虑时的扫描和维护已知信息的思想都是解决本题的关键。
这种解法似乎复杂度也有点高,但是实际上还是挺快的,78ms,还有其他的做法可以解决此题,单调栈、轮廓线思想等等,但都是从计算贡献的角度出发的。
#include 14、hdu 4035 Maze
传送门
题意:有n个房间,由n-1条隧道连通起来形成一棵树,从结点1出发,开始走,在每个结点i都有3种可能:
1.被杀死,回到结点1处(概率为ki)
2.找到出口,走出迷宫 (概率为ei)
3.和该点相连有m条边,随机走一条
求:走出迷宫所要走的边数的期望值。
分析:经典题,值得一做。
本题的期望dp是很清晰的,令dp[i]为当前在i号房间时走出迷宫的期望边数。
dp[i]=kidp[1]+ei∗0+(1−ki−ei)∗(dp[fa[i]]+1m+∑dp[child[i]]+1m) d p [ i ] = k i d p [ 1 ] + e i ∗ 0 + ( 1 − k i − e i ) ∗ ( d p [ f a [ i ] ] + 1 m + ∑ d p [ c h i l d [ i ] ] + 1 m ) ;如果i为叶子节点,那么 dp[i]=kidp[1]+ei∗0+(1−ki−ei)∗dp[fa[i]]+1m d p [ i ] = k i d p [ 1 ] + e i ∗ 0 + ( 1 − k i − e i ) ∗ d p [ f a [ i ] ] + 1 m ,n<=10000,我们建立了方程组之后高斯消元显然不可行。注意到一个问题,节点i只与1号节点,子节点、父节点有关系,而叶子节点只与1号节点和父节点有关,我们尝试另外表示方程组。
设 dp[i]=Ai∗dp[1]+Bi∗dp[father[i]]+Ci; d p [ i ] = A i ∗ d p [ 1 ] + B i ∗ d p [ f a t h e r [ i ] ] + C i ;
建立对于非叶子结点i,设j为i的孩子结点,则
∑(dp[child[i]])=∑dp[j]=∑(Aj∗dp[1]+Bj∗dp[father[j]]+Cj)=∑(Aj∗dp[1]+Bj∗dp[i]+Cj) ∑ ( d p [ c h i l d [ i ] ] ) = ∑ d p [ j ] = ∑ ( A j ∗ d p [ 1 ] + B j ∗ d p [ f a t h e r [ j ] ] + C j ) = ∑ ( A j ∗ d p [ 1 ] + B j ∗ d p [ i ] + C j )
代入上面的式子得
由此可得
对于叶子节点, Ai=ki;Bi=1−ki−ei;Ci=1−ki−ei; A i = k i ; B i = 1 − k i − e i ; C i = 1 − k i − e i ;
我们从叶子节点开始往上计算,最终可以求得dp[1]。
本题的关键在于树结构下找到方程组之间的联系,并化简方程组,递推得出方程组的解。
#include 到这里,算是总结完了~