从零开始学贪心算法

贪心算法的定义：
贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。
解题的一般步骤是：
1.建立数学模型来描述问题；
2.把求解的问题分成若干个子问题；
3.对每一子问题求解，得到子问题的局部最优解；
4.把子问题的局部最优解合成原来问题的一个解。
如果大家比较了解动态规划，就会发现它们之间的相似之处。最优解问题大部分都可以拆分成一个个的子问题，把解空间的遍历视作对子问题树的遍历，则以某种形式对树整个的遍历一遍就可以求出最优解，大部分情况下这是不可行的。贪心算法和动态规划本质上是对子问题树的一种修剪，两种算法要求问题都具有的一个性质就是子问题最优性(组成最优解的每一个子问题的解，对于这个子问题本身肯定也是最优的)。动态规划方法代表了这一类问题的一般解法，我们自底向上构造子问题的解，对每一个子树的根，求出下面每一个叶子的值，并且以其中的最优值作为自身的值，其它的值舍弃。而贪心算法是动态规划方法的一个特例，可以证明每一个子树的根的值不取决于下面叶子的值，而只取决于当前问题的状况。换句话说，不需要知道一个节点所有子树的情况，就可以求出这个节点的值。由于贪心算法的这个特性，它对解空间树的遍历不需要自底向上，而只需要自根开始，选择最优的路，一直走到底就可以了。
话不多说，我们来看几个具体的例子慢慢理解它：
1.活动选择问题
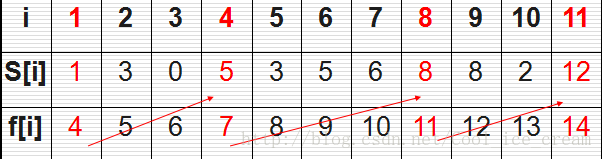
这是《算法导论》上的例子，也是一个非常经典的问题。有n个需要在同一天使用同一个教室的活动a1,a2,…,an，教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后，活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠，ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。例如下图所示的活动集合S，其中各项活动按照结束时间单调递增排序。

考虑使用贪心算法的解法。
可以用数学归纳法证明，我们的贪心策略应该是每次选取结束时间最早的活动。直观上也很好理解，按这种方法选择相容活动为未安排活动留下尽可能多的时间。这也是把各项活动按照结束时间单调递增排序的原因。
解析：默认从早上开始排，结束的早剩下的就能多放点，参考1-5，6-8和4-7；

#include
#include 
#include 
using namespace std;    
int N;
struct Act
{
    int start;
    int end;
}act[100010];

bool cmp(Act a,Act b)  
{  
    return a.endint greedy_activity_selector()  
{  
    int num=1,i=1;   
    for(int j=2;j<=N;j++)  
    {  
        if(act[j].start>=act[i].end)  
        {  
            i=j;  
            num++;  
        }  
    }  
    return num;
}

int main()  
{  
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&N);
        for(int i=1;i<=N;i++)
        {
            scanf("%lld %lld",&act[i].start,&act[i].end);
        }
        act[0].start=-1;
        act[0].end=-1;
        sort(act+1,act+N+1,cmp); 
        int res=greedy_activity_selector();
        cout<

2.小船过河问题
POJ1700是一道经典的贪心算法例题。题目大意是只有一艘船，能乘2人，船的运行速度为2人中较慢一人的速度，过去后还需一个人把船划回来，问把n个人运到对岸，最少需要多久。先将所有人过河所需的时间按照升序排序，我们考虑把单独过河所需要时间最多的两个旅行者送到对岸去，有两种方式：
1.最快的和次快的过河，然后最快的将船划回来；次慢的和最慢的过河，然后次快的将船划回来，所需时间为：t[0]+2*t[1]+t[n-1]；
2.最快的和最慢的过河，然后最快的将船划回来，最快的和次慢的过河，然后最快的将船划回来，所需时间为：2*t[0]+t[n-2]+t[n-1]。
算一下就知道，除此之外的其它情况用的时间一定更多。每次都运送耗时最长的两人而不影响其它人，问题具有贪心子结构的性质。
AC代码：

#include
#include
using namespace std;

int main()
{
    int a[1000],t,n,sum;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        sum=0;
        for(int i=0;i"%d",&a[i]);
        while(n>3)
        {
            sum=min(sum+a[1]+a[0]+a[n-1]+a[1],sum+a[n-1]+a[0]+a[n-2]+a[0]);
            n-=2;
        }
        if(n==3) sum+=a[0]+a[1]+a[2];
        else if(n==2) sum+=a[1];
        else sum+=a[0];
        printf("%d\n",sum);
    }
}

3.销售比赛
在学校OJ上做的一道比较好的题，这里码一下。假设有偶数天，要求每天必须买一件物品或者卖一件物品，只能选择一种操作并且不能不选，开始手上没有这种物品。现在给你每天的物品价格表，要求计算最大收益。首先要明白，第一天必须买，最后一天必须卖，并且最后手上没有物品。那么除了第一天和最后一天之外我们每次取两天，小的买大的卖，并且把卖的价格放进一个最小堆。如果买的价格比堆顶还大，就交换。这样我们保证了卖的价格总是大于买的价格，一定能取得最大收益。

#include
#include
#include
#include
#include
#include
#include
using namespace std;
long long int price[100010],t,n,res;

int main()
{
    ios::sync_with_stdio(false);
    cin>>t;
    while(t--)
    {
        cin>>n;
        priority_queue<long long int, vector<long long int>, greater<long long int> > q;
        res=0;
        for(int i=1;i<=n;i++)
        {
            cin>>price[i];
        }
        res-=price[1];
        res+=price[n];
        for(int i=2;i<=n-1;i=i+2)
        {
            long long int buy=min(price[i],price[i+1]);
            long long int sell=max(price[i],price[i+1]);
            if(!q.empty())
            {
                if(buy>q.top())
                {
                    res=res-2*q.top()+buy+sell;
                    q.pop();
                    q.push(buy);
                    q.push(sell);
                }
                else
                {
                    res=res-buy+sell;
                    q.push(sell);
                }
            }
            else
            {
                res=res-buy+sell;
                q.push(sell);
            }
        }     
        cout<

4.Dijkstra算法
Dijkstra算法是由E.W.Dijkstra于1959年提出，是目前公认的最好的求解最短路径的方法，使用的条件是图中不能存在负边。算法解决的是单个源点到其他顶点的最短路径问题，其主要特点是每次迭代时选择的下一个顶点是标记点之外距离源点最近的顶点，简单的说就是bfs+贪心算法的思想。

#include
#include 
#define INF 1000 
#define MAX_V 100
using namespace std;  

int main()
{
    int V,E;
    int i,j,m,n;
    int cost[MAX_V][MAX_V];
    int d[MAX_V];
    bool used[MAX_V];
    cin>>V>>E;
    fill(d,d+V+1,INF);
    fill(used,used+V,false);
    for(i=0;ifor(j=0;jif(i==j) cost[i][j]=0;
            else cost[i][j]=INF;
        }
    }
    for(m=0;mcin>>i>>j>>cost[i][j];
        cost[j][i]=cost[i][j];
    }
    cin>>n;
    d[n]=0;
    //源点 
    while(true)
    {
        int v=V;
        for(m=0;mif((!used[m])&&(d[m]if(v==V) break;
        used[v]=true;
        for(m=0;mfor(i=0;icout<<"the shortest distance between "<" and "<" is "<