【FJWC】day4简要题解

T1.循环流

一堆特判

if(a>0 && ((a%2==0 && n>2)||(a%2==1))) putchar('1');

写成了

if(a>0 && ((a%2==0 && a>2)||(a%2==1))) putchar('1');

100pts$\to$ 35pts！
我服我自己！

#include
using namespace std;

int tk,n,a,b;

int main(){
//	freopen("flow.in","r",stdin);
//	freopen("flow.out","w",stdout);
	for(scanf("%d%d",&a,&tk);tk;--tk){
		scanf("%d%d%d",&n,&a,&b);
		if(n-1>a+b) putchar('0');
		else if((!a)||(!b)){
			a=a+b-(n-1);
			if(a>0 && ((a%2==0 && n>2)||(a%2==1))) putchar('1');
			else putchar('0');
		}else if(b<n-1){
			a-=(n-1-b);if(a>1) putchar('1');else putchar('0');
		}else{
			if(b>n-1){
				if((b-n)%2==0 || n>2){
				   if((a%2==0) || (a%2==1 && a>1 && n>2)) putchar('1');
				   else putchar('0');
				}else{
				   if(a%2==0 && a>1) putchar('1');
				   else putchar('0');
				}
			}else{
				if(a<2) putchar('0');
				else if(a%2==0 || n>2) putchar('1');
				else putchar('0');
			}
		}
		if(tk>1) putchar('\n');
	}
	fclose(stdin);fclose(stdout);
	return 0;
}

---

T2.整除分块

究极找规律神题：

首先不出现在$\lfloor \frac{n}{i}\rfloor$的数$k$一定满足：
$\lfloor \frac{n}{\lfloor \frac{n}{k}\rfloor }\rfloor >k\to n\%k\ge \lfloor \frac{n}{k}\rfloor ,k>\lfloor \sqrt{n}\rfloor$

故$k$不出现的数的区间：

$[ai+a,ai+i-1](1\le a<i)$即：

$[i+1,2i-1],[2i+2,3i-1],...,[i^2-1,i^2-1]$

(╯▽╰)好吧还是需要打表，忽略过程直接讲规律吧：

首先把$f(n)$序列划分成$[(i-1{)}^2,i^2-1]$的段。

发现每段($x\ast y$表示数$x$重复出现$y$次)：

倒着看前$i-1$个数长这样：
$i\ast 2,(i+1)\ast 4,(i+2)\ast 6,(i+3)\ast 8...$
是个递增的每个数出现次数按偶数次递增的等差数列($2,4,6,8...$)

倒着看后$i$个数长这样：
$i\ast 1,(i+1)\ast 3,(i+2)\ast 5,(i+3)\ast 7...$
是个递增的每个数出现次数按奇数次递增的等差数列($1,3,5,7...$)

吐槽：这谁发现得了啊，摔(就算发现了$O(n)$也只有$30pts$)

然后大力计算：

拿奇数等差数列举例：

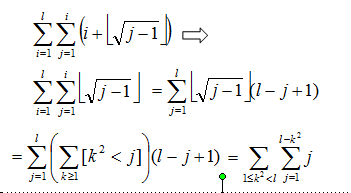
枚举以$i$开头的等差数列，长度为$i$，第$j$个数是$i+\lfloor \sqrt{j-1}\rfloor$。

实话说我又化了一下式子还是没看懂std在求啥。

std:

#include 
#include 
#include 
#include 
using namespace std;
typedef __int128 LL;
const int mo=998244353;
const int inv2=499122177;
const int inv6=166374059;
const int inv4=748683265;
const int inv30=432572553;
LL l,r;
char s[100];
__int128 Read() {
    __int128 x=0;
    scanf("%s",s);
    int len=strlen(s);
    for (int i=0;i<len;i++)
        x=x*10+s[i]-48;
    return x;
}
int Sum(int x,int y) {
    x+=y;
    return (x>=mo)?x-mo:x;
}
int Sub(int x,int y) {
    x-=y;
    return (x<0)?x+mo:x;
}
int Mul(int x,int y) {
    return (long long)x*y%mo;
}
LL Ex_Sqrt(LL x,int ty) {
    LL l=0,r=2e18;
    while (l<r) {
        LL mid=(l+r+1)/2;
        LL nowf=mid*mid;
        if (ty==1) nowf-=mid+1;
        else if (ty==2) nowf+=mid;
        if (nowf<=x) l=mid;
        else r=mid-1;
    }
    return l;
}
int T(int x,int ty) {
    if (ty==1) return Mul(Mul(x,Sum(x,1)),inv2);
    if (ty==2) return Mul(Mul(Mul(x,Sum(x,1)),Sum(Sum(x,x),1)),inv6);
    if (ty==3) return Mul(Mul(Mul(x,x),Mul(Sum(x,1),Sum(x,1))),inv4);        
    int nowx=Sub(Mul(3,Sum(Mul(x,x),x)),1);
    return Mul(Mul(Mul(x,Mul(Sum(x,1),Sum(Sum(x,x),1))),nowx),inv30);
}
namespace task1 {
    int F1(LL n) {
        LL nx=Ex_Sqrt(n,0)%mo;
        int nown=n%mo;
        int ans=Mul(nown,Mul(Sum(nown,1),nx));
        ans=Sum(Sub(ans,Mul(T(nx,2),Sum(Sum(nown,nown),1))),T(nx,4));
        return Mul(ans,inv2);
    }
    int F2(LL k) {
        int nowk=Ex_Sqrt(k,0)%mo;
        return Sub(Mul(k%mo,nowk),T(nowk,2));
    }
    int Get(LL k,LL n) {
        if (k*k-k>n) return 0;
        LL lx=k*k-n;
        return Sub(Sum(Mul(k%mo,(k-lx+1)%mo),F2(k)),F2(lx-1));
    }
    int Solve(LL n) {
        LL nx=Ex_Sqrt(n+1,0);
        return Sum(Sum(T(nx%mo,2),F1(nx)),Get(nx+1,n));
    }
}
namespace task2 {
    int F1(LL n) {
        LL nx=Ex_Sqrt(n,2)%mo;
        int nown=n%mo;
        int ans=Sum(T(nx,4),Mul(2,T(nx,3)));
        ans=Sub(ans,Mul(Sum(nown,Sub(nown,2)),T(nx,2)));
        ans=Sub(ans,Mul(Sum(nown,Sub(nown,1)),T(nx,1)));
        ans=Sum(ans,Mul(Mul(nown,Sub(nown,1)),nx));
        return Mul(ans,inv2);
    }
    int F2(LL k) {
        LL nowk=Ex_Sqrt(k,2)%mo;
        return Sub(Mul(k%mo,nowk),Sum(T(nowk,2),T(nowk,1)));
    }
    int Get(LL k,LL n) {
        if ((k-1)*(k-1)>n) return 0;
        LL lx=k*k-k-n;
        return Sub(Sum(Mul(k%mo,(k-lx)%mo),F2(k-1)),F2(lx-1));
    }
    int Solve(LL n) {
        LL nx=Ex_Sqrt(n,1);
        return Sum(Sum(Sub(T(nx%mo,2),T(nx%mo,1)),F1(nx)),Get(nx+1,n));
    }
}
int Solve(LL n) {
    return Sum(task1::Solve(n),task2::Solve(n));
}
int t,Test;
int main() {
	freopen("mex.in","r",stdin);
	freopen("mex.out","w",stdout);
    scanf("%d%d",&Test,&t);
    while (t--) {
        l=Read();
        r=Read();
        printf("%d\n",Sub(Solve(r),Solve(l-1)));
    }
    return 0;
}

---

T3.森林

题目等价于找到一条直径，且满足直径伸出去的第三条链(第三叉)最长。

出题人有个高级的叫法：三叉戟

设加叶子之前直径为$u,v$，存在一下性质：

• 加入后直径只可能为$(u,x),(v,x),(u,v)$
• 第三叉的长度只增不减

比较显然就不证了。

所以算法流程就是维护一条直径$(u,v)$以及一个第三叉长度$mx$，每次加入一个点$x$，如果在直径里，那么将其加入直径，第三叉长度不变，否则利用$x$到直径的路径长度来更新第三叉长度。 输出时直接输出$dis(u,v)+mx-(mx̸=0)$即可。

大力LCT：

std

$multiset$维护虚儿子最长链(第三叉)
$MX$维护路径上最长第三叉
$LMX$维护实链根向下最长链
$RMX$用于换根时$swap(LMX,RMX)$

#include 
using namespace std;

const int N = 4e5 + 5;

int ch[N][2], S[N], n, m, x, y, fa[N], Size[N], MAXL[N], MAX[N], L, R, nowDis, MAXR[N];
bool rev[N];
multiset <int> Xs[N];

#define lc (ch[x][0])
#define rc (ch[x][1])

bool isroot(int x) {
  return ch[fa[x]][1] != x && ch[fa[x]][0] != x;
}

bool dir(int x) {
  return ch[fa[x]][1] == x;
}

#define Erase(x, y) x.erase(x.find(y))

int get(multiset <int> &S, int Rk) {
  if(S.size() < Rk) return 0;
  multiset < int > :: reverse_iterator it = S.rbegin();
  for(int i = 1; i < Rk; ++ i) ++ it;
  return *it;
}

void pd(int x);

void up(int x) {
  pd(x);
  Size[x] = Size[lc] + Size[rc] + 1;
  MAX[x] = max(get(Xs[x], 1), max(MAX[lc], MAX[rc]));
  MAXL[x] = max(Size[lc] + max(get(Xs[x], 1), Size[rc]), max(MAXL[lc], MAXL[rc] + Size[lc] + 1));
  MAXR[x] = max(Size[rc] + max(get(Xs[x], 1), Size[lc]), max(MAXR[rc], MAXR[lc] + Size[rc] + 1));
}

void add(int x, int y, int val) {
  if(val == 1) {
    Xs[x].insert(MAXL[y] + 1);
    up(x);
    return;
  }
  else {
    Erase(Xs[x], MAXL[y] + 1);
    up(x);
    return;
  }
}

void rotate(int x) {
  int F = fa[x], GF = fa[F], Dx = dir(x), Df = dir(F), Son = ch[x][!Dx];
  if(!isroot(F)) ch[GF][Df] = x;
  fa[x] = GF; fa[F] = x; if(Son) fa[Son] = F;
  ch[F][Dx] = Son; ch[x][!Dx] = F;
  up(F); up(x);
}

void pt(int x) {
  if(!x) return;
  swap(lc, rc);
  rev[x] ^= 1;
  swap(MAXL[x], MAXR[x]);
}

void pd(int x) {
  if(rev[x]) {
    pt(lc);
    pt(rc);
    rev[x] = 0;
    up(x);
  }
}

void put(int x) {
  if(!isroot(x)) put(fa[x]);
  pd(x);
}

void splay(int x) {
  put(x);
  while(!isroot(x)) {
    if(isroot(fa[x])) return (void)rotate(x);
    if(dir(x) == dir(fa[x])) rotate(fa[x]), rotate(x);
    else rotate(x), rotate(x);
  }
}

void access(int x) {
  int t = 0;
  while(x) {
    splay(x);
    if(rc) {
      add(x, rc, 1);
    }
    if(t) {
      add(x, t, -1);
    }
    rc = t;
    up(x);
    t = x, x = fa[x];
  }
}

void makeroot(int x) {
  access(x);
  splay(x);
  pt(x);
}

void link(int x, int y) {
  makeroot(x);  makeroot(y);
  fa[x] = y;
  add(y, x, 1);
  pd(y);
}

//void cut(int x, int y) {
//  makeroot(x);
//  access(y); access(x);
//  add(x, y, -1);
//}

int query(int x, int y) {
  makeroot(x);
  access(y);
  splay(y);
  return max(Size[y] + MAX[y] - 2, Size[y] - 1);
}

int Qdis(int x, int y) {
  makeroot(x);
  access(y);
  splay(y);
  return Size[y] - 1;
}

void re(int x, int y, int w) {
  int dA = Qdis(x, y), dB = Qdis(x, w), dC = Qdis(y, w);
  L = x, R = y;
  if(dB > dA) L = x, R = w, dA = dB;
  if(dC > dA) L = w, R = y, dA = dC;
}

int main() {
  freopen("forest.in","r",stdin);
  freopen("forest.out","w",stdout);
  int t; cin >> t;
  MAXL[0] = MAXR[0] = MAX[0] = -1e9;
  cin >> n;
  up(1);
  L = 1, R = 1, nowDis = 0;
  for(int i = 2; i <= n; ++ i) {
    up(i);
    int x; scanf("%d", &x); x ^= nowDis;
    link(x, i);
    re(L, R, i);
    printf("%d\n", nowDis = query(L, R));
  }
}

---

总结

总体来说T1,3都在正常难度范围之内。
也就是说把会做的能做的部分都拿满成绩已经不错了——
然而T1一个字母之差(过了大样例就跑了)WA了65pts。
全程肝T2导致T3没有时间仔细思考…

实际上T2花再多时间(即使把结论推出来了)得分上限也是30，不如看一下一看就很传统可得分的数据结构T3…

主要问题在于时间分配和代码稳定性。