吴恩达深度学习(二)-第一周(2):Regularization
Regularization
# import packages
import numpy as np
import matplotlib.pyplot as plt
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
import sklearn
import sklearn.datasets
import scipy.io
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
Problem Statement: You have just been hired as an AI expert by the French Football Corporation. They would like you to recommend positions where France’s goal keeper should kick the ball so that the French team’s players can then hit it with their head.
The goal keeper kicks the ball in the air, the players of each team are fighting to hit the ball with their head
They give you the following 2D dataset from France’s past 10 games.
train_X, train_Y, test_X, test_Y = load_2D_dataset()
Each dot corresponds to a position on the football field where a football player has hit the ball with his/her head after the French goal keeper has shot the ball from the left side of the football field.
- If the dot is blue, it means the French player managed to hit the ball with his/her head
- If the dot is red, it means the other team’s player hit the ball with their head
Your goal: Use a deep learning model to find the positions on the field where the goalkeeper should kick the ball.
Analysis of the dataset: This dataset is a little noisy, but it looks like a diagonal line separating the upper left half (blue) from the lower right half (red) would work well.
You will first try a non-regularized model. Then you’ll learn how to regularize it and decide which model you will choose to solve the French Football Corporation’s problem.
1 - Non-regularized model
You will use the following neural network (already implemented for you below). This model can be used:
- in regularization mode – by setting the
lambdinput to a non-zero value. We use “lambd” instead of “lambda” because “lambda” is a reserved keyword in Python. - in dropout mode – by setting the
keep_probto a value less than one
You will first try the model without any regularization. Then, you will implement:
- L2 regularization – functions: “
compute_cost_with_regularization()” and “backward_propagation_with_regularization()” - Dropout – functions: “
forward_propagation_with_dropout()” and “backward_propagation_with_dropout()”
In each part, you will run this model with the correct inputs so that it calls the functions you’ve implemented. Take a look at the code below to familiarize yourself with the model.
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)
learning_rate -- learning rate of the optimization
num_iterations -- number of iterations of the optimization loop
print_cost -- If True, print the cost every 10000 iterations
lambd -- regularization hyperparameter, scalar
keep_prob - probability of keeping a neuron active during drop-out, scalar.
Returns:
parameters -- parameters learned by the model. They can then be used to predict.
"""
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
Let’s train the model without any regularization, and observe the accuracy on the train/test sets.
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
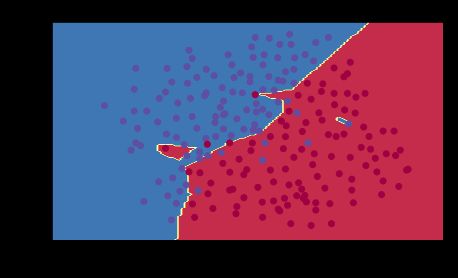
The train accuracy is 94.8% while the test accuracy is 91.5%. This is the baseline model (you will observe the impact of regularization on this model). Run the following code to plot the decision boundary of your model.
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
# 这里x.T把 生成的坐标数据 转置 传入函数中
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y.ravel())
The non-regularized model is obviously overfitting the training set. It is fitting the noisy points! Lets now look at two techniques to reduce overfitting.
2 - L2 Regularization
The standard way to avoid overfitting is called L2 regularization. It consists of appropriately modifying your cost function, from:
(1) J = − 1 m ∑ i = 1 m ( y ( i ) log ( a [ L ] ( i ) ) + ( 1 − y ( i ) ) log ( 1 − a [ L ] ( i ) ) ) J = -\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} \tag{1} J=−m1i=1∑m(y(i)log(a[L](i))+(1−y(i))log(1−a[L](i)))(1)
To:
(2) J r e g u l a r i z e d = − 1 m ∑ i = 1 m ( y ( i ) log ( a [ L ] ( i ) ) + ( 1 − y ( i ) ) log ( 1 − a [ L ] ( i ) ) ) ⎵ cross-entropy cost + 1 m λ 2 ∑ l ∑ k ∑ j W k , j [ l ] 2 ⎵ L2 regularization cost J_{regularized} = \small \underbrace{-\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} }_\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W_{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{2} Jregularized=cross-entropy cost −m1i=1∑m(y(i)log(a[L](i))+(1−y(i))log(1−a[L](i)))+L2 regularization cost m12λl∑k∑j∑Wk,j[l]2(2)
Let’s modify your cost and observe the consequences.
Exercise: Implement compute_cost_with_regularization() which computes the cost given by formula (2). To calculate ∑ k ∑ j W k , j [ l ] 2 \sum\limits_k\sum\limits_j W_{k,j}^{[l]2} k∑j∑Wk,j[l]2 , use :
np.sum(np.square(Wl))
Note that you have to do this for W [ 1 ] W^{[1]} W[1], W [ 2 ] W^{[2]} W[2] and W [ 3 ] W^{[3]} W[3], then sum the three terms and multiply by $ \frac{1}{m} \frac{\lambda}{2} $.
# GRADED FUNCTION: compute_cost_with_regularization
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
Implement the cost function with L2 regularization. See formula (2) above.
Arguments:
A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
parameters -- python dictionary containing parameters of the model
Returns:
cost - value of the regularized loss function (formula (2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
### START CODE HERE ### (approx. 1 line)
L2_regularization_cost = 1./m * lambd/2. * (np.square(W1).sum()+np.square(W2).sum()+np.square(W3).sum())
### END CODER HERE ###
cost = cross_entropy_cost + L2_regularization_cost
return cost
A3, Y_assess, parameters = compute_cost_with_regularization_test_case()
print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1)))
Expected Output:
| **cost** | 1.78648594516 |
Of course, because you changed the cost, you have to change backward propagation as well! All the gradients have to be computed with respect to this new cost.
Exercise: Implement the changes needed in backward propagation to take into account regularization. The changes only concern dW1, dW2 and dW3. For each, you have to add the regularization term’s gradient ( d d W ( 1 2 λ m W 2 ) = λ m W \frac{d}{dW} ( \frac{1}{2}\frac{\lambda}{m} W^2) = \frac{\lambda}{m} W dWd(21mλW2)=mλW).
# GRADED FUNCTION: backward_propagation_with_regularization
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
Implements the backward propagation of our baseline model to which we added an L2 regularization.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation()
lambd -- regularization hyperparameter, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
### START CODE HERE ### (approx. 1 line)
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
### END CODE HERE ###
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
### START CODE HERE ### (approx. 1 line)
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
### END CODE HERE ###
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
### START CODE HERE ### (approx. 1 line)
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
### END CODE HERE ###
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd = 0.7)
print ("dW1 = "+ str(grads["dW1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("dW3 = "+ str(grads["dW3"]))
Expected Output:
| **dW1** | [[-0.25604646 0.12298827 -0.28297129] [-0.17706303 0.34536094 -0.4410571 ]] |
| **dW2** | [[ 0.79276486 0.85133918] [-0.0957219 -0.01720463] [-0.13100772 -0.03750433]] |
| **dW3** | [[-1.77691347 -0.11832879 -0.09397446]] |
Let’s now run the model with L2 regularization ( λ = 0.7 ) (\lambda = 0.7) (λ=0.7). The model() function will call:
compute_cost_with_regularizationinstead ofcompute_costbackward_propagation_with_regularizationinstead ofbackward_propagation
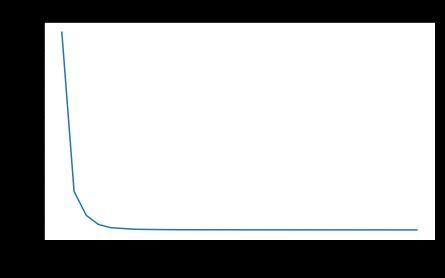
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
Cost after iteration 0: 0.6974484493131264
Cost after iteration 10000: 0.2684918873282239
Cost after iteration 20000: 0.26809163371273004
On the train set:
Accuracy: 0.9383886255924171
On the test set:
Accuracy: 0.93
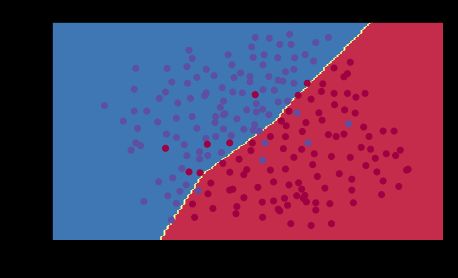
Congrats, the test set accuracy increased to 93%. You have saved the French football team!
You are not overfitting the training data anymore. Let’s plot the decision boundary.
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y.flatten())
Observations:
- The value of λ \lambda λ is a hyperparameter that you can tune using a dev set.
- L2 regularization makes your decision boundary smoother. If λ \lambda λ is too large, it is also possible to “oversmooth”, resulting in a model with high bias.
3 - Dropout
Finally, dropout is a widely used regularization technique that is specific to deep learning.
It randomly shuts down some neurons in each iteration. Watch these two videos to see what this means!
At each iteration, you shut down (= set to zero) each neuron of a layer with probability $1 - keep\_prob$ or keep it with probability $keep\_prob$ (50% here). The dropped neurons don't contribute to the training in both the forward and backward propagations of the iteration.
$1^{st}$ layer: we shut down on average 40% of the neurons. $3^{rd}$ layer: we shut down on average 20% of the neurons.
When you shut some neurons down, you actually modify your model. The idea behind drop-out is that at each iteration, you train a different model that uses only a subset of your neurons. With dropout, your neurons thus become less sensitive to the activation of one other specific neuron, because that other neuron might be shut down at any time.
3.1 - Forward propagation with dropout
Exercise: Implement the forward propagation with dropout. You are using a 3 layer neural network, and will add dropout to the first and second hidden layers. We will not apply dropout to the input layer or output layer.
Instructions:
You would like to shut down some neurons in the first and second layers. To do that, you are going to carry out 4 Steps:
- In lecture, we dicussed creating a variable d [ 1 ] d^{[1]} d[1] with the same shape as a [ 1 ] a^{[1]} a[1] using
np.random.rand()to randomly get numbers between 0 and 1. Here, you will use a vectorized implementation, so create a random matrix $D^{[1]} = [d^{1} d^{1} … d^{1}] $ of the same dimension as A [ 1 ] A^{[1]} A[1]. - Set each entry of D [ 1 ] D^{[1]} D[1] to be 0 with probability (
1-keep_prob) or 1 with probability (keep_prob), by thresholding values in D [ 1 ] D^{[1]} D[1] appropriately. Hint: to set all the entries of a matrix X to 0 (if entry is less than 0.5) or 1 (if entry is more than 0.5) you would do:X = (X < 0.5). Note that 0 and 1 are respectively equivalent to False and True. - Set A [ 1 ] A^{[1]} A[1] to A [ 1 ] ∗ D [ 1 ] A^{[1]} * D^{[1]} A[1]∗D[1]. (You are shutting down some neurons). You can think of D [ 1 ] D^{[1]} D[1] as a mask, so that when it is multiplied with another matrix, it shuts down some of the values.
- Divide A [ 1 ] A^{[1]} A[1] by
keep_prob. By doing this you are assuring that the result of the cost will still have the same expected value as without drop-out. (This technique is also called inverted dropout.)
# GRADED FUNCTION: forward_propagation_with_dropout
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
### START CODE HERE ### (approx. 4 lines) # Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0], A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
### START CODE HERE ### (approx. 4 lines)
D2 = np.random.rand(A2.shape[0], A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
X_assess, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob = 0.7)
print ("A3 = " + str(A3))
A3 = [[0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]]
Expected Output:
| **A3** | [[ 0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]] |
3.2 - Backward propagation with dropout
Exercise: Implement the backward propagation with dropout. As before, you are training a 3 layer network. Add dropout to the first and second hidden layers, using the masks D [ 1 ] D^{[1]} D[1] and D [ 2 ] D^{[2]} D[2] stored in the cache.
Instruction:
Backpropagation with dropout is actually quite easy. You will have to carry out 2 Steps:
- You had previously shut down some neurons during forward propagation, by applying a mask D [ 1 ] D^{[1]} D[1] to
A1. In backpropagation, you will have to shut down the same neurons, by reapplying the same mask D [ 1 ] D^{[1]} D[1] todA1. - During forward propagation, you had divided
A1bykeep_prob. In backpropagation, you’ll therefore have to dividedA1bykeep_probagain (the calculus interpretation is that if A [ 1 ] A^{[1]} A[1] is scaled bykeep_prob, then its derivative d A [ 1 ] dA^{[1]} dA[1] is also scaled by the samekeep_prob).
# GRADED FUNCTION: backward_propagation_with_dropout
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
### START CODE HERE ### (≈ 2 lines of code)
dA2 *= D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 /= keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ2 = np.multiply(dA2, np.int64(A2 > 0)) # np.int64(A2 > 0) means relu gradient
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
### START CODE HERE ### (≈ 2 lines of code)
dA1 *= D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 /= keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob = 0.8)
print ("dA1 = " + str(gradients["dA1"]))
print ("dA2 = " + str(gradients["dA2"]))
dA1 = [[ 0.36544439 0. -0.00188233 0. -0.17408748]
[ 0.65515713 0. -0.00337459 0. -0. ]]
dA2 = [[ 0.58180856 0. -0.00299679 0. -0.27715731]
[ 0. 0.53159854 -0. 0.53159854 -0.34089673]
[ 0. 0. -0.00292733 0. -0. ]]
Expected Output:
**dA2**
[[ 0.58180856 0. -0.00299679 0. -0.27715731]
**dA1**
[[ 0.36544439 0. -0.00188233 0. -0.17408748] [ 0.65515713 0. -0.00337459 0. -0. ]]
[ 0. 0.53159854 -0. 0.53159854 -0.34089673]
[ 0. 0. -0.00292733 0. -0. ]]
Let’s now run the model with dropout (keep_prob = 0.86). It means at every iteration you shut down each neurons of layer 1 and 2 with 24% probability. The function model() will now call:
forward_propagation_with_dropoutinstead offorward_propagation.backward_propagation_with_dropoutinstead ofbackward_propagation.
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
Cost after iteration 0: 0.6543912405149825
Cost after iteration 10000: 0.0610169865749056
Cost after iteration 20000: 0.060582435798513114
On the train set:
Accuracy: 0.9289099526066351
On the test set:
Accuracy: 0.95
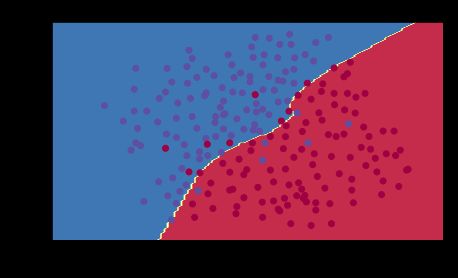
Dropout works great! The test accuracy has increased again (to 95%)! Your model is not overfitting the training set and does a great job on the test set. The French football team will be forever grateful to you!
Run the code below to plot the decision boundary.
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y.flatten())
Note:
- A common mistake when using dropout is to use it both in training and testing. You should use dropout (randomly eliminate nodes) only in training.
- Deep learning frameworks like tensorflow, PaddlePaddle, keras or caffe come with a dropout layer implementation. Don’t stress - you will soon learn some of these frameworks.
4 - Conclusions
Here are the results of our three models:
3-layer NN without regularization
95%
91.5%
3-layer NN with L2-regularization
94%
93%
3-layer NN with dropout
93%
95%
| **model** | **train accuracy** | **test accuracy** |
Note that regularization hurts training set performance! This is because it limits the ability of the network to overfit to the training set. But since it ultimately gives better test accuracy, it is helping your system.
Congratulations for finishing this assignment! And also for revolutionizing French football.
**What we want you to remember from this notebook**: - Regularization will help you reduce overfitting. - Regularization will drive your weights to lower values. - L2 regularization and Dropout are two very effective regularization techniques.