数学形态学(mathematical morphology)关注的是图像中的形状,它提供了一些方法用于检测形状和改变形状。起初是基于二值图像提出的,后来扩展到灰度图像。二值图像就是:每个像素的值只能是0或1,1代表描绘图像的点,0代表背景。
基本的形态学运算包括:腐蚀(erosion)、膨胀(dilation)、开(opening)、闭(closing),对于这些运算,都需要用到被称为结构元素(Structuring element)的模板,一般为方形,以小矩阵的形式表示,但它的元素的值只能是0或1,它代表的是一个集合,这个集合罩在原图像上,可以跟原图像的形状进行集合运算。
腐蚀(erosion)
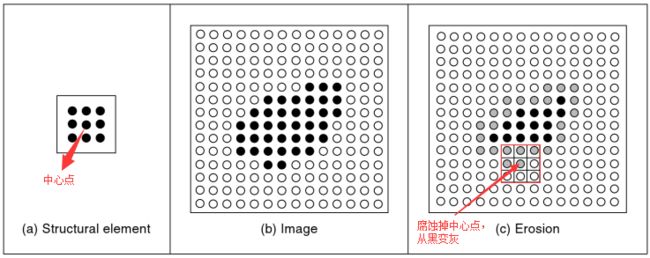
图中(a)为原图像,(b)为腐蚀运算后结果,可以看出除了字母笔刷变细了之外,黑色背景的噪点也都不见了,(c)是膨胀运算结果,字母笔刷比原图像粗。
如图所示,(a)是3×3结构元素,相当于:
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])图中标识出了它的中心点。
结构元素的设置也可以是其它大小,也不一定全是1(黑点),比如是一个3×3十字形:
[[0,1,0],
[1,1,1],
[0,1,0]](b)为待处理的原图像,我们把其中由所有黑点组成的集合设为X
(c)为腐蚀后的结果,黑色点就是经过腐蚀之后保留下来的点,灰色的点表示被排除出去的点,我们看到的效果是X变小了一圈,这也之所以叫腐蚀的原因吧。
可以这样来形象理解腐蚀运算过程:将结构元素平移到原图像上某个位置,如果结构元素中所有的黑点(值为1)都落在X里,就把结构元素中心点对应的原图像的像素点保留下来,否则就排除出去,如(c)所示,假设结构元素盖在这个位置,这时结构元素下半部还有几个点没落在原图X中,所以将中心点对应的像素点排除出去,从黑色标记为灰色。将结构元素在原图像上进行平移,直到原图像的每一个像素都被处理过。
所以这个结果也会把形状以外的噪点排除掉。
腐蚀函数说明
scipy.ndimage.morphology.binary_erosion(input, structure=None, iterations=1,...)
input: 原图像二值图
structure: 即结构元素,默认为3×3十字形
iterations: 表示要连续应用腐蚀多少次
返回腐蚀后二值图结果,ndarray类型示例:
>>> a = np.zeros((7,7), dtype=np.int)
>>> a[1:6, 2:5] = 1
>>> a #原图像二值图,注意中间由1组成的矩形形状
array([[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])
>>> ndimage.binary_erosion(a).astype(a.dtype)
#可以看出矩形形状被"腐蚀"了一圈
array([[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]]) 膨胀(dilation)
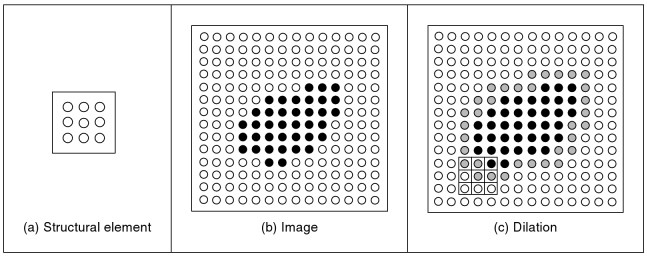
如图(c)就是膨胀的结果,运算过程跟腐蚀类似,只不过对像素的排除判断不一样,膨胀的判断方式是:只要结构元素中有一个黑点(值为1)落在X集合里,就把结构元素中心点对应的原图像的像素点保留下来,否则就排除出去。
膨胀函数scipy.ndimage.morphology.binary_dilation与腐蚀类似,使用示例:
>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> a
array([
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
>>> ndimage.binary_dilation(a).astype(a. dtype) #binary_dilation第二个参数可指定结构元素,默认为3×3十字形
array([
[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 1., 1., 1., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.]])我们从以上的效果图可以看到,腐蚀和膨胀可以改变形状,同时也可以去背景噪点。
另外,把形状的膨胀结果减去它的腐蚀结果,可以得到形状的粗略边缘以及角点。
开(opening)
先对原图像进行腐蚀,再膨胀,就是开运算。有什么用呢?简单点说它可以去除与结构元素大小相当的孔洞和碎片。如果一处图像中有多个形状,开运算可以把那些只有一点点粘连的形状分开。因为那点粘连的地方被去除了。
简单示例:
>>> a = np.zeros((5,5), dtype=np.int)
>>> a[1:4, 1:4] = 1; a[4, 4] = 1
>>> a #原图像,注意右下角有个1,表示零散的碎片
array([[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 1]])
>>> ndimage.binary_opening(a, structure=np.ones((3,3))).astype(np.int)
array([[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]]) #基于3×3全1的结构元素应用开运算,把原图像角落的1去掉
>>> ndimage.binary_opening(a).astype(np.int)
array([[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0]]) #还可以用于平滑边角,也就是四角处缩小变平滑了,如果形状与形状有边角的粘连,就可以分开闭(closing)
与开运算相反,先对原图进行膨胀,再腐蚀,就是闭运算。闭运算可以填充图像中的孔洞,连接一些缺口和碎片,变成块状。举个应用场景——车牌定位,如下图:
右图是使用通过简单的算法得到车的粗略边角,车牌位置像是一堆散点,如果对这个边角图运用闭运算可以得到这样的效果: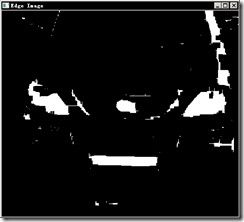
车牌的位置变成一个接近车牌形状的矩形,为下一步检测提供了便利。
闭运算函数ndimage.binary_closing的用法:
>>> a = np.zeros((5,5), dtype=np.int)
>>> a[1:-1, 1:-1] = 1; a[2,2] = 0
>>> a #原图像,注意中间有个0,表示形状里面有个空洞
array([[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 0, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]])
>>> ndimage.binary_closing(a).astype(np.int)
array([[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]]) #应用闭运算之后,空洞被填充了开闭运算原理看似简单,但很强大,只要结构元素选取得当,可以做很多事情。
对象计数(Counting Objects)
这里说的对象是指图像中与周围没有连通的单独的形状,我们的目标是要计算这些对象的个数,计算对象个数可以使用函数:
label, num_features = scipy.ndimage.measurements.label(input, structure=None, output=None)
参数
input: 数组类型,其中元素非0值表示对象组成的点,0表示图像背景
structure: 结构元素,用于检测对象的连通特征,默认是3×3十字形
返回值
label: 返回与input一样的大小,但是把对象标记出来
num_features:对象的个数用法简单示例:
>>> a = np.array([[0,0,1,1,0,0],
... [0,0,0,1,0,0],
... [1,1,0,0,1,0],
... [0,0,0,1,0,0]])
>>> labeled_array, num_features = measurements.label(a) #使用默认3×3十字形结构元素
>>> print(num_features)
4
>>> print(labeled_array) #打印被识别出来的对象的位置,分别用1,2,3...递增的下标标记出来,所以labeled_array可以当成灰度图打印出来,被标识的对象的灰度从黑到白变化
array([[0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 0, 0],
[2, 2, 0, 0, 3, 0],
[0, 0, 0, 4, 0, 0]])从上面例子看出,使用默认3×3十字形结构元素,检测时,只有水平和垂直连通才认为像素属于同一个对象,对角连通不算,如果要把对角连通当作是同一个对象来计算,可以指定结构元素为:
[[1,1,1],
[1,1,1],
[1,1,1]]有时候,因受噪声影响,对象之间有一点边角的粘连,人眼可以很容易分辨出是两个对象,但要让label函数理解这一点,可以使用前面提到的开运算先对把对象稍微分开,再把结果传给label函数进行计数,下面给出一个具体的图像进行示例:
from PIL import Image
import numpy as np
from scipy.ndimage import measurements,morphology
import matplotlib.pyplot as plt
im = np.array(Image.open('house.png').convert('L'))
im = 1 * (im < 128) #把灰度图像转为二值图,即灰度少于128的当成图像黑点,否则当作背景
label_from_origin, num_from_origin = measurements.label(im)
im_open = morphology.binary_opening(im, np.ones((9, 5)), iterations=2) #运用了一个9×5全1的结构元素,并连续应用两次开运算
label_from_open, num_from_open = measurements.label(im_open)
#以下是画图
index = 221
plt.subplot(index)
plt.imshow(im)
plt.title('original')
plt.axis('off')
plt.subplot(index + 1)
plt.imshow(label_from_origin)
plt.title('%d objects' % num_from_origin)
plt.axis('off')
plt.subplot(index + 2)
plt.imshow(im_open)
plt.title('apply opening')
plt.axis('off')
plt.subplot(index + 3)
plt.imshow(label_from_open)
plt.title('%d objects' % num_from_open)
plt.axis('off')
#plt.gray() #为了更好的看出对象的分离,故意不用灰度显示
plt.show()效果图如下,第二组(即第二行)是应用开运算之后的图像及计算结果,跟第一组相比,对象计数增加了,我在第二组图中圈出了应用开运算之后的主要变化之处:
小结
上面介绍的用于二值图的一些函数,也有其对应的用于灰度图像的函数,包括:
grey_erosion()
grey_dilation()
grey_opening()
grey_closing()
下一节学习图像去噪。
你还可以查看其它笔记。
参考资料
图像的膨胀与腐蚀
数学形态学基本操作及其应用
《计算机视觉特征提取与图像处理(第三版)》