多标签学习综述

多标签学习综述（A review on multi-label learning algorithms）

2014 TKDE(IEEE Transactions on Knowledge and Data Engineering)

张敏灵，周志华

简单介绍

传统监督学习主要是单标签学习，而现实生活中目标样本往往比较复杂，具有多个语义，含有多个标签。本综述主要介绍了多标签学习的一些相关内容，包括相关定义，评价指标，8个多标签学习算法，相关的其它任务。

论文大纲

1. 相关定义：学习任务，三种策略
2. 评价指标：基于样本的评价指标，基于标签的评价指标
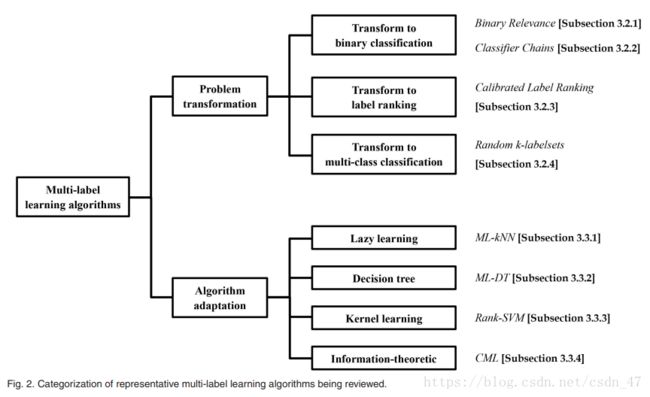
3. 学习算法：介绍了8个有代表性的算法，4个基于问题转化的算法和4个基于算法改进的算法
4. 相关任务：多实例学习，有序分类，多任务学习，数据流学习

相关定义

学习任务

$X={\mathbb{R}}^d$表示d维的输入空间，$Y=\{y_1,y_2,...,y_q\}$ 表示带有q个可能标签的标签空间。

训练集 $D=(x^i,y^i)|1\le i\le m$ ，m表示训练集的大小，上标表示样本序数，有时候会省略。

$x^i\in X$ ，是一个d维的向量。$y^i\subseteq Y$ ，是 $Y$ 的一个标签子集。

任务就是要学习一个多标签分类器 $h(\cdot )$，预测 $h(x)\subseteq Y$作为x的正确标签集。

常见的做法是学习一个衡量x和y相关性的函数 $f(x,y_j)$，希望 $f(x,y_{j1})>f(x,y_{j2})$ ，其中 $y_{j1}\in y,y_{j2}\notin y$。

$h(x)$ 可以由 $f(x)$ 衍生得到 $h(x)=\{y_j|f(x,y_j)>t(x),y_j\in Y\}$。 $t(x)$ 扮演阈值函数的角色，把标签空间对分成相关的标签集和不相关的标签集。

阈值函数可以由训练集产生，可以设为常数。当 $f(x,y_j)$ 返回的是一个概率值时，阈值函数可设为常数0.5。

三种策略

多标签学习的主要难点在于输出空间的爆炸增长，比如20个标签，输出空间就有 $2^{20}$，为了应对指数复杂度的标签空间，需要挖掘标签之间的相关性。比方说，一个图像被标注的标签有热带雨林和足球，那么它具有巴西标签的可能性就很高。一个文档被标注为娱乐标签，它就不太可能和政治相关。有效的挖掘标签之间的相关性，是多标签学习成功的关键。根据对相关性挖掘的强弱，可以把多标签算法分为三类。

• 一阶策略：忽略和其它标签的相关性，比如把多标签分解成多个独立的二分类问题（简单高效）。
• 二阶策略：考虑标签之间的成对关联，比如为相关标签和不相关标签排序。
• 高阶策略：考虑多个标签之间的关联，比如对每个标签考虑所有其它标签的影响（效果最优）。

评价指标

略

学习算法

可分为两类（具体算法如下图所示）

• 问题转换的方法：把多标签问题转为其它学习场景，比如转为二分类，标签排序，多分类
• 算法改编的方法：通过改编流行的学习算法去直接处理多标签数据，比如改编懒学习，决策树，核技巧。
  

Binary Relevance

把多个标签分离开来，对于q个标签，建立q个数据集和q个二分类器来进行预测。
这是最简单最直接的方法，是其它先进的多标签算法的基石。
没有考虑标签之间的关联性，是一个一阶策略（first-order）

Classifier Chains

首先按特定的顺序（这个顺序是自己决定的）对q个标签排个序，得到yτ(1)≻yτ(2)≻…≻yτ(q)。对于第j个标签yτ(j)构建一个二分类的数据集。
$$\begin{gathered} D_{\tau (j)}=\{([x^i,pr{e}_{\tau (j)}^i],1\{y_{\tau (j)}\in y^i\})|1\le i\le m\} \\ wherepr{e}_{\tau (j)}^i=(1\{y_{\tau (1)}\in y^i\},...,1\{y_{\tau (j-1)}\in y^i\}{)}^T \end{gathered}$$
第j个标签构建的二分类数据集中，$x^i$ 会concat上前j-1个标签值。
以这样chain式的方法构建q个数据集，训练q个分类器。
在预测阶段，由于第j个分类器需要用到前j-1个分类器预测出的标签集，所以需要顺序调用这q个分类器来预测。

1. 显然算法的好坏会受到顺序τ的影响，可以使用集成的方式，使用多个随机序列，对每个随机序列使用一部分的数据集进行训练。
2. 虽然该算法把问题分解成多个二分类，但由于它以随机的方式考虑了多个标签之间的关系，所以它是一个高阶策略（high-order）。
3. 该算法的一个缺点是丢失了平行计算的机会，因为它需要链式调用来进行预测

Calibrated Label Ranking

算法的基本思想是把多标签学习问题转为标签排序问题，该算法通过“成对比较”来实现标签间的排序。
对q个标签，可以构建q(q-1)/2个标签对，所以可以构建q(q-1)/2个数据集。
$$\begin{gathered} D_{jk}=\{(x_i,\psi (y^i,y_j,y_k))|\varphi (y^i,y_j)̸=\varphi (y^i,y_k),1\le i\le m\} \\ where\psi (y^i,y_j,y_k))=\{\begin{array}{cc}+1,& if\varphi (y^i,y_j)=+1and\varphi (y^i,y_k)=-1\\ -1,& if\varphi (y^i,y_j)=-1and\varphi (y^i,y_k)=+1\end{array} \\ \varphi (y^i,y_j)=\{\begin{array}{cc}+1& if{y}_j\in y^i\\ -1& else\end{array} \end{gathered}$$

1. 只有带有不同相关性的两个标签 $y_j$ 和 $y_k$ 的样本才会被包含在数据集 $D_{jk}$ 中，用该数据集训练一个分类器，当分类器返回大于0时，样本属于标签 $y_j$ ，否则属于标签 $y_k$。
2. 可以看到，每个样本 $x_i$ 会被包含在 $\left|y^i\right|\left|\overline{y^i}\right|$ 个分类器中。
3. 在预测阶段，根据分类器，每个样本和某个标签会产生一系列的投票，根据投票行为来做出最终预测。
4. 前面构造二分类器的方法使用one-vs-rest的方式，本算法使用one-vs-one，缓和类间不均衡的问题。
5. 缺点在于复杂性高，构建的分类器个数为 $q(q-1)/2$，表现为二次增长。
6. 考虑两个标签之间的关联，是二阶策略（second-order）

Random k-Labelsets

算法的基本思想是把多标签学习问题转为多分类问题。把 $2^q$ 个可能的标签集，映射成 $2^q$ 个自然数。
映射函数记为 ${\sigma }_Y$ ，则原数据集变为
$$D_Y^{+}=(x^i,{\sigma }_Y(y^i))|1\le i\le m$$
所对应的新类别记为
$$\Gamma (D_Y^{+})={\sigma }_Y(y^i)|1\le i\le m，\left|\Gamma (D_Y^{+})\right|\le min(m,2^{|Y|})$$
这样来训练一个多分类器，最后根据输出的自然数映射回标签集的算法称为LP（Label Powerest）算法，它有两个主要的局限性

1. LP预测的标签集是训练集中已经出现的，它没法泛化到未见过的标签集
2. 类别太大，低效

为了克服LP的局限性，Random k-Labelsets使用的LP分类器只训练Y中的一个长度为k的子集，然后集成大量的LP分类器来预测。
$Y^k$ 表示 $Y$ 的所有的长度为 $k$ 的子集，$Y^k(l)$ 表示随机取的一个长度为 $k$ 的子集，这样就可以进行收缩样本空间，得到如下样本集和标签集。
$$D_{Y^k(l)}^{+}=\{(x^i,{\sigma }_{Y^k(l)}(y^i\cap Y^k(l)))|1\le i\le m\}$$
$$\Gamma (D_{Y^k(l)}^{+})=\{{\sigma }_{Y^k(l)}(y^i\cap Y^k(l))|1\le i\le m\}$$
更进一步，我们随机取n个这样的子集：
$$Y^k(l_r),1\le r\le n$$
来构造n个分类器做集成。
最后预测的时候需要计算两个指标，一个为标签j能达到的最大投票数，一个为实际投票数。
$$\tau (x,y_j)=\sum _{r=1}^{n}1\{y_j\in Y^k(l_r)\}$$
$$\mu (x,y_j)=\sum _{r=1}^{n}1\{y_j\in {\sigma }_{Y^k(l)}^{-1}(g_{Y^k(l)}^{+}(x))\}$$
其中$ \sigma_{Y^k(l)}{-1}(\cdot)表示从自然数映射回标签集的函数，g^+(\cdot)$表示分类器学习到的函数。最后预测的时以0.5为阈值进行预测，得到标签集。
$$y=\{y_j|\mu (x,y_j)/\tau (x,y_j)>0.5,1\le j\le q\}$$
因为是随机长度为k的子集，考虑了多个标签之间的相关性，所以是高阶策略（high-order）。

Multi-Label k-Nearest Neighbor（ML-KNN）

用 $N(x)$ 表示 $x$ 的 $k$ 个邻居，则 $C_j=\sum (x,y)\in N(x)1yj\in y$ 表示样本 $x$ 的邻居中带有标签$y_j$的邻居个数。 用 $H_j$ 表示样本 $x$ 含有标签 $y_j$ ，根据后验概率最大化的规则，有
$$y=\{y_j|P(H_j|C_j)/P(┐H_j|C_j)>1,1\le j\le q\}$$
根据贝叶斯规则，有
$$\frac{P(H_j|C_j)}{P(┐H_j|C_j)}=\frac{P(H)\cdot P(C_j|H_j)}{P(┐H)\cdot P(C_j|H_j)}$$
先验概率 $P(H_j),P(┐H_j)$ 可以通过训练集计算得到，表示样本带有或不带有标签 $y_q$ 的概率
$$\begin{gathered} P(H_j)=\frac{s+{\sum }_{i=1}^{m}1\{y_j\in y^i\}}{s\times 2+m} \\ P(┐H_j)=1-P(H_j)(1\le j\le q) \end{gathered}$$
其中s是平滑因子，s为1时则使用的是拉普拉斯平滑。
条件概率的计算需要用到两个值
$$\begin{gathered} {\kappa }_j[r]=\sum _{i=1}^{m}1\{y_j\in y^i\}\cdot 1\{{\delta }_j(x^i)=r\}(0\le r\le k) \\ {\tilde{\kappa }}_j[r]=\sum _{i=1}^{m}1\{y_j\notin y^i\}\cdot 1\{{\delta }_j(x^i)=r\}(0\le r\le k) \\ where{\delta }_j(x^i)=\sum _{(x^{\ast },y^{\ast })\in N(x^i)}1\{y_j\in y^{\ast }\} \end{gathered}$$
${\kappa }_j[r]$表示“含有标签 $y_j$而且 $r$ 个邻居也含有标签 $y_j$ 的”样本的个数。
${\tilde{\kappa }}_j[r]$表示“不含有标签$y_j$ 但是 $r$ 个邻居含有 $y_j$ 的”样本的个数。
根据这两个值，可以计算相应的条件概率
$$\begin{gathered} P(C_j|H_j)=\frac{s+{\kappa }_j[C_j]}{s\times (k+1)+{\sum }_{r=0}^k{\kappa }_j[r]}(1\le j\le q,0\le C_j\le k) \\ P(C_j|┐H_j)=\frac{s+{\tilde{\kappa }}_j[C_j]}{s\times (k+1)+{\sum }_{r=0}^k{\tilde{\kappa }}_j[r]}(1\le j\le q,0\le C_j\le k) \end{gathered}$$

这两个条件概率表示的是，样本带有或不带有标签 $y_j$ 的条件下，它有 $C_j$ 个邻居带有标签$y_j$ 的概率。

1. 由上述的条件概率，先验概率则可以根据贝叶斯规则和后验概率最大化，计算出样本的标签集
2. 需要注意的是该方法不是KNN和独立二分类的简单结合，因为算法中还使用了贝叶斯来推理邻居信息
3. 没有考虑标签之间的相关性，是一阶策略（first-order）

Multi-Label Decision Tree（ML-DT）

使用决策树的思想来处理多标签数据，数据集$T$中，使用第$l$个特征，划分值为 $\vartheta$，计算出如下信息增益：
$$\begin{gathered} IG(T,l,\vartheta )=MLEnt(T)-\sum _{\rho \in \{-,+\}}\frac{|T^{\rho }|}{\left|T\right|}\cdot MLEnt(T^{\rho }) \\ where{T}^{-}=\{(x^i,y^i)|x_{il}\le v,1\le i\le n\} \\ where{T}^{+}=\{(x^i,y^i)|x_{il}>v,1\le i\le n\} \end{gathered}$$

递归地构建一颗决策树，每次选取特征和划分值，使得上式的信息增益最大。
其中式子中的熵的公式可以按如下计算（为了方便计算，假定标签之间独立）。
$$\begin{gathered} MLEnt(T)=\sum _{j=1}^q-p_{j}lo{g}_2{p}_j-(1-p_j)lo{g}_2(1-p_j) \\ where{p}_j=\frac{{\sum }_{i=1}^{n}1\{y_j\in y^i\}}{n} \end{gathered}$$

1. 新样本到来时，向下遍历决策树的结点，找到叶子结点，若pj大于0.5则表示含有标签yj
2. 该算法不是决策树和独立二分类的简单结合（如果是的话，应该构建q棵决策树）
3. 没有考虑标签的相关性，是一阶策略（first-order）

Ranking Support Vector Machine（Rank-SVM）

使用最大间隔的思想来处理多标签数据。
Rank-SVM考虑系统对相关标签和不相关标签的排序能力。
考虑最小化 $x^i$ 到每一个“相关-不相关”标签对的超平面的距离，来得到间隔。
$$\underset{(x^i,y^i)\in D}{\min }\underset{(y_j,y_k)\in y^i\times \overline{y^i}}{\min }\frac{⟨w_j-w_k,x^i⟩+b_j-b_k}{\Vert w_j-w_k\Vert }$$
像SVM一样对w和b进行缩放变换后可以对式子进行改写，然后最大化间隔，再调换分子分母进行改写，得到：
$$\begin{array}{cc}{\min }_w& {\max }_{1\le j<k\le q}{\Vert w_j-w_k\Vert }^2\\ subjectto:& ⟨w_j-w_k,x^i⟩+b_j-b_k\ge 1\\ & (1\le i\le m,(y_i,y_k)\in y^i\times \overline{y^i})\end{array}$$
为了简化，用sum操作来近似max操作
$$\begin{array}{cc}{\min }_w& {\sum }_{j=1}^q{\Vert w_j\Vert }^2\\ subjectto:& ⟨w_j-w_k,x^i⟩+b_j-b_k\ge 1\\ & (1\le i\le m,(y_i,y_k)\in y^i\times \overline{y^i})\end{array}$$

跟SVM一样，为了软间隔最大化，引入松弛变量，得到下式：
$$\begin{gathered} \begin{array}{cc}{\min }_{w,\Xi }& {\sum }_{j=1}^q{\Vert w_j\Vert }^2+C{\sum }_{i=1}^m\frac{1}{|y^i||\overline{y^i}|}{\sum }_{(y_i,y_k)\in y^i\times \overline{y^i})}{\xi }_{ijk}\\ subjectto:& ⟨w_j-w_k,x^i⟩+b_j-b_k\ge 1-{\xi }_{ijk}\\ & {\xi }_{ijk}>0(1\le i\le m,(y_i,y_k)\in y^i\times \overline{y^i})\end{array} \\ 其中\Xi =\{{\xi }_{ijk}|1\le i\le m,(y_i,y_k)\in y^i\times \overline{y^i}\} \end{gathered}$$

1. 跟SVM一样，最终的式子是一个二次规划问题，通常调用现有的包来解。
2. 对于非线性问题则使用核技巧来解决。
3. 由于定义了”相关-不相关“标签对的超平面，这是个二阶策略（second-order）

Collective Multi-Label Classifier（CML）

该算法的核心思想最大熵原则。用 $(x,y)$ 表示任意的一个多标签样本，其中 $y=(y_1,y_2,...,y_q)\in \{-1,+1{\}}^q$ 算法的任务等价于学习一个联合概率分布 $p(x,y)$ ，用$H_p(x,y)$ 表示给定概率分布 $p$ 时 $(x,y)$ 的信息熵。最大熵原则认为熵最大的模型是最好的模型。
$$\begin{array}{cc}& {\max }_p{H}_p(x,y)\\ & subjectto:E_p[f_k(x,y)]=F_k(k\in K)\end{array}$$
其中 $f_k(x,y)$ 是一个特征函数，描述 $x$ 和 $y$ 之间的一个事实 $k$ ，满足这个事实时返回1，否则返回0。约束做的是希望这个分布上，特征函数的期望能够等于一个我们希望的值 $F_k$，这个值通常通过训练集来估计。解这个优化问题，会得到
$$p(y|x)=\frac{1}{Z_{\Lambda }(x)}exp(\sum _{k\in K}{\lambda }_k\cdot f_k(x,y))$$
其中$\Lambda =\lambda k|k\in K$表示一系列的权重。$Z_{\Lambda }={\sum }_{y}exp({\sum }_{k\in K}{\lambda }_k\cdot f_k(x,y))作为规范化因子。假设有一个高斯先验{\lambda }_k\sim N(0,{\epsilon }^2)，就可以通过最大化以下这个log后验概率来求得参数\Lambda$。
$$\begin{array}{cc}l(\Lambda |D)& =logP(D|\Lambda )+logP(\Lambda )\\ & =log{\prod }_{(x,y)\in D}p(y|x)+logP(\Lambda )\\ & =log({\prod }_{(x,y)\in D}p(y|x))-{\sum }_{k\in K}\frac{{\lambda }^2}{2{\epsilon }^2}\end{array}$$

1. 这是个凸函数，可以调用现成的无约束优化方法比如BFGS直接求解。求得参数就可以得到要学习的概率分布 $p(y|x)$。
2. 对于一系列约束K，分为两个部分
3. $K_1=\{(l,j)|1\le l\le d,1\le j\le q\}$，有 $d\cdot q$ 个约束，特征函数为
   $$f_k(x,y)=x_l\cdot 1\{y_j==1\},k=(l,j)\in K_1$$
4. $K_2=(j_1,j_2,b_1,b_2)|1\le j_1<j_2\le q,b_1,b_2\in -1,+1$，有 $4\cdot \left(\genfrac{}{}{0ex}{}{q}{2}\right)$ 个约束，特征函数为
   $$f_k(x,y)=1\{y_{j1}=b_1\}\cdot 1\{y_{j2}=b_2\},k=(j_1,j_2,b_1,b_2)\in K_2$$
5. 由于K约束中考虑了标签对之间的关联，该算法是个二阶策略（second-order）。

相关任务

1. 多实例学习（Multi-instance learning）：每个样本由多个实例和一个标签组成，多个实例中至少一个为正，认为该样本为正。和多标签学习的输出空间模糊相反，多实例学习是输入空间模糊。
2. 有序分类（Ordinal classification）：对于每个标签，不再是简单地判断是还是否，而是改成一系列的等级排序，把yj={−1,+1}替换成yj={m1,m2,…,mk}, where m1
3. 多任务学习（Multi-task learning）：同时训练多个任务，相关任务之间的训练信息会帮助其它任务。比如目标定位既要识别有没有目标（分类问题）又要定位出目标的位置（回归问题）。
4. 数据流学习（Data streams classification）：真实世界的目标是在线生成和实时产生的，如何处理这些数据就是数据流学习要做的事。一个关键的挑战就是“概念漂移”（目标变量的统计特性随着时间的推移以不可预见的方式变化），一般处理方式有：当一大批新数据到来时更新分类器；维持一个检测器来警惕概念漂移；假定过去数据的影响会随着时间而衰减。

总结

1. 论文主要介绍了多标签学习的一些概念定义，策略，评价指标，以及8个有代表性的算法，其中对多种评价指标和多个算法都做了清晰的分类和详细的阐述。
2. 尽管挖掘标签关联性的想法被应用到许多算法中，但是仍然没有一个正式的机制。有研究表示多标签之间的关联可能是非对称的（我对你的影响和你对我的影响是不同的），局部的（不同样本之间的标签相关性不同，很少关联性是所有样本都满足的）。
3. 但是不管怎么说，充分理解和挖掘标签之间的相关性，是多标签学习的法宝。尤其是巨大输出空间场景下。